村上定瞭(水浄化フォーラム)
Ⅰ.コロイドと界面現象
1.コロイドとは
2.疎水・親水コロイド
3.疎水コロイドの分散と凝集
4.親水コロイドの塩析
5.会合コロイドとミセル
6.コロイド溶液の物性
Ⅱ.解説
解説(A) 粒子界面の静電気現象
解説(B) 疎水性2粒子系の相互作用
解説(C) 粒子界面電荷の発生
解説(D) 電解質効果とSchulze-Hardy法則
解説(E) 凝集速度
解説(F) 表面張力と界面活性
解説(G) 界面活性剤の特性
解説(H) 吸着エネルギーと平衡式
解説(J) 高分子吸着と分散・凝集
付録 疎水コロイド相互作用の計算ソフト
(ダウンロード)
参考文献
関連ページ
分散・懸濁粒子の凝集分離
Ⅱ.解 説
解説(A) 粒子界面の静電気現象
<イオン数濃度>
n(= n∞):母液中の電解質の個数濃度[/m3]、
n+・n–:拡散二重層内における正・負イオンの個数濃度[/m3]、
z:z-z型電解質のイオン価数、e:素量電荷(1.60×10-19[C])、
k:ボルツマン定数(1.38×10-23[J/K])、T:絶対温度[K]
<Poisson式>
ρ:電荷密度[C/m3]、ε:水の誘電率
<電荷密度>
= nze{exp[-zeΨ/(kT)] – exp[zeΨ/(kT)]}
= – 2nze・sinh[zeΨ/(kT)] (A-2)
<電位変化>
式(A-3)を x = ∞ (Ψ = 0) ~ x = 0 (Ψ= Ψo) の範囲で積分すると、次式が得られる。
γ = tanh[zeΨo/(4kT)] (A-5)
式(A-4)を変形すると、界面電位Ψoを有する荷電粒子の表面から距離x(x≦a)における電気二重層の電位Ψ(x)は、次式で示される。
式(A-6)が求めるΨ(x)であるが、特に電位の低いzeΨo≪4kT(25℃で4zeΨo≪104mV)であるならば、式(A-6)のln[1 + γexp(-κx)]/[1 – γexp(-κx)] = 2γexp(-κx)となる(Debye-Hukel近似)ので、次式のように簡略化される。
したがって、式(A-3)は、次式のように簡易化される。
式(A-8)を、式(A-4)を求めた同じ範囲で積分すると、式(A-4)の近似式として、次式が得られる。
<留意事項>
以上のような理由により、水浄化分野における分散粒子の数量的取扱いにおいて、疎水性コロイド粒子に対しては、その挙動や傾向は近似式(Ⅰ-7)・(Ⅰ-8)で概略的な説明が可能である。疎水性粒子についての数量的取扱いは、前編Ⅰ-3や本解説(A)・(B)で記載しているが、疎水性でない粒子の界面近傍の数量的扱いについては、複雑となるので省略する。
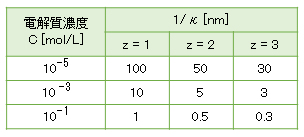
<電気二重層の厚さ>
z-z型電解質の濃度と電気二重層の厚さを表A-1に示す。 2価・3価の金属イオンは配位水を有し、pHの上昇により酸解離してOH–が配位した錯イオンを形成し、予想される1/κよりも大きい値となることに留意する(詳しくは、解説(D)-1.電解質効果)。
目次へ
解説(B) 疎水性2粒子系の相互作用
なお、コロイドに関する本モデルは、次の条件に限定したものとする。
・水溶液内の荷電粒子は球状で、表面電位Ψoとする。ただし、単原子イオンなどÅレベルの小さなイオンが特異吸着している場合には、Stern電位ΨδをΨoとする(図B-1を参照)。
・荷電粒子は疎水性とし、粒子表面に水和層の形成はなく、さらに、特異的に吸着する複雑なイオン(界面活性剤イオン、高分子イオン、高原子価イオン、錯イオンなど)は共存しないものとする。
・水溶液内に共存する正負イオンはz-z価の対称電解質が完全解離したものとする。
・電気二重層の厚さ(1/κ)は10nm以下(例えば、NaCl濃度>1mmol/L)で、ここで扱う粒子の半径 aは100nm~1μm程度とすると、2粒子が接近してそれらの電気二重層が重なったとき、その重なり領域に対応する粒子表面は近似的に平面(具体的には円板)として扱うことができるものとする(a≫1/κ)。
<電気二重層のモデル>
Helmholtzは金属表面の電荷と、これを中和する溶液中のイオンが向かい合って並んでいるいて、これを平行コンデンサーが形成されるようなモデルを考えこれを電気二重層と呼んだ(図B-1・A)。
次に、イオンには熱運動を行って均一に分布する作用が働く。したがって、界面近傍の過剰な対イオンは、重力場内の分散系粒子の沈降平衡に似た拡散的な分布をとる。このことから、二重層内の電位低下は界面付近で急激で、界面から遠ざかるにつれてなだらかとなる。これをGouy-Chapmanの拡散二重層のモデルである(図B-1・B)。
しかし、このような拡散二重層のみによって計算した値は、測定値よりも一桁大きく、むしろHelmholtzのモデルによる値がずっと測定値に近い。この矛盾を解決するために、Sternは金属表面のすぐ近くにはイオンの特異吸着(Stern層)があって、この外側にGouy-Chapmanの拡散二重層が広がっているようなモデルを考えた(図B-1・C・D)。
このような表面の電荷と帯電粒子の固定相、および拡散二重層を総括して界面電気二重層と呼ばれる。本モデルで取り扱う対称は、この図中の(B)または(C)とする。
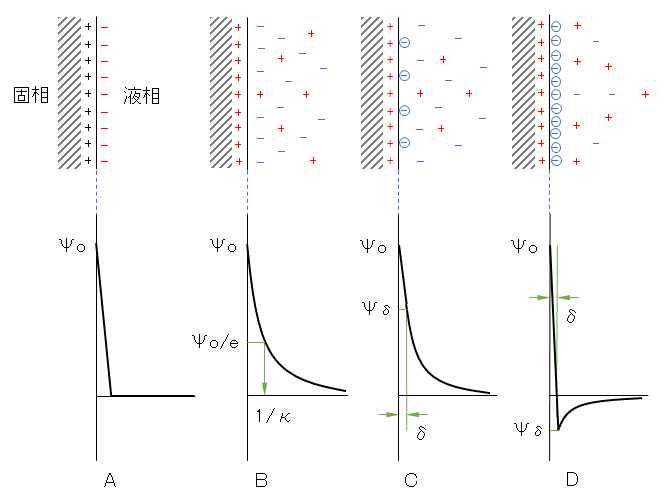
図B-1 粒子と電解質溶液の界面近傍における電気二重層のモデル
<コロイド粒子の分散と凝集>
粒子間には、静電気的反発力(分散力)PR [N/m2]とvan der Waals引力(凝集力)PA [N/m2]の2つの相互作用が働き、これらの合力は次式で示される。
一方で、コロイド系の安定性は、その系の状態を分散エネルギーVR[J]および凝集エネルギーVA [J]を総和した自由エネルギーVに依存する。
本章の冒頭に記載した電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m](<a)に接近したときの相互作用力P(h)および自由エネルギーV(h)は、次式で近似的に示される。
P(h) = 2πaεκΨo2 exp(-κh) – aA/(12h2) (Ⅰ-7)
V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8)
κ2 = 2nz2e2/(εkT) (Ⅰ-9)
κ = 3.3×109z√C [/m] (T = 298K) (Ⅰ-10)
ここで、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、25℃)、A:Hamaker定数、z:z-z型対称電解質の価数、n:単位体積中の電解質イオン個数[1/m3](n = n∞:図Ⅰ-5・C、参照)である。
なお、25℃の水溶液では、電荷質濃度C[mol/L]とすると、n = 103NAC[/m3] (NA:Avogadro定数、6.02×1023[/mol))であるので、式(Ⅰ-9)は式(Ⅰ-10)で示される。
式(Ⅰ-7)・式(Ⅰ-8)に基づいて、試算した結果の事例を図Ⅰ-6~図Ⅰ-8に示した。これらの式の導入過程にあっては様々な近似と簡略化が行われているが、コロイド粒子の水溶液中における挙動の概要を説明できる。以下に、これらの式の導入過程について解説する。詳しくは、ページボトムに記載の参考文献(北原・渡辺, 1972、北原, 1994や粉体工学会, 2010など)を参照されたい。
<計算ソフト>
1.荷電粒子間の静電相互作用
しかし、2つの粒径粒子の二重層の重なりによる自由エネルギーの増加量の計算はかなり複雑である。そこで、粒子径 a(100nm以上)が二重層の厚さκ(10nm前後)の10倍以上、すなわち、a≫1/κであれば、二重層の重なりを2枚の同符号に荷電した平行板に近似して扱うことができる(電気回路で多用されるコンデンサーの極板は正負の対符号で帯電していることが大きな相違である)。多くの場合、この近似モデルでその概略を満足に説明できる結果が導かれる。
ここで、2枚の同サイズ・同符号に帯電の平行板の単位面積あたりに働くは力Pp[N/m2]は式(B-1)に示すように静電気力Peと浸透圧Poの和となり、PeとPoは、それぞれ式(B-2)および(B-3)で示される。
Pp = Pe + Po (B-1)
Pe = -(ε/2) (dΨ/dx)2 (B-2)
Po = (n+ + n–)kT – 2nkT (B-3)
一般に、Poは常にPeよりも大きく、さらに二重層の重なりによって表面電位Ψoに変化がなければ、Peを無視できる。この理由は、同サイズで同符号に帯電した平行板であれば、それらの中間距離での面上では、その対称性から電界[V/m]はdΨ/dx = 0となり、Poのみを考えればよいこととなる。
1.1 荷電平行板の静電相互作用(Derjaguin近似)
Pp(h) = 2nkT{cosh[zeΨ(h/2)/(kT)] – 1} (B-4)
h:2平行板間の距離[m]、Ψ(h/2):中間点における電位[V]
式(B-4)は複雑であるので、以下に示す近似を行う。
電位が低く、また電位の重なりが余り大きくない条件では、図B-2に示すように、式(A-6)で表される単独粒子の電気二重層の電位Ψ(h/2)の2倍に相当するものと考えると、Ψp(h/2) = 2Ψ(h/2)、となる。
次に、zeΨ/4kT≪1の時には、解説(A)の式(A-7)の近似式にx = h/2を代入すると、次式が得られる。
Ψp(h/2) = 2Ψ(h/2) = 8kT/(ze)・γexp(-κh/2) (B-5)
γ= tanh[zeΨo/(4kT)] (A-5)
ここで、 式(B-4)の右辺のcosh項についてテイラー展開して3次項までの近似、cosh y ≒ 1 + (1/2)y2、を用い、この近似式に式(B-5)を代入すると、次式が得られる。
cosh[zeΨ(h/2)/(kT)] ≒ 1 + (1/2)[zeΨp(h/2)/(kT)]2
= 1 + 32γ2exp(-κh)
上式を式(B-4)に代入すると、次式で示される。
Pp(h) = 64nkTγ2 exp(-κh) (B-6)
以上のことから、同サイズの2枚の平衡した荷電平行板を遠距離∞からhまで接近させたときの単位面積あたりの必要エネルギーVp[J/m2]は、式(B-6)を積分すると、次式で表される。
Vp(h) = -∫Pp(h)dh (h = ∞ → h) = (64nkTγ2/κ)exp(-κh) (B-7)
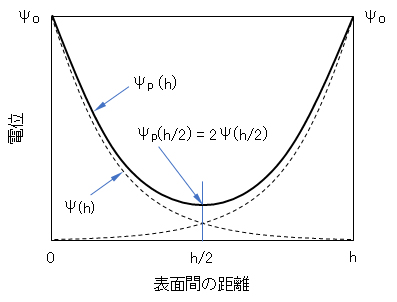
図B-2 同符号に荷電した2枚の平行板による電気二重層の重なり
1.2 2粒子間にはたらく静電相互作用
図Ⅰ-5・Dに示すように、本モデルの条件(a≫1/κ)では電気二重層の厚さが小さいので、Deriaguin近似を導入して球を半径 aの薄い円板と考えると、この2枚の円板間の静電相互作用力FR(h)は、次式で示される。
FR(h) = 2π{a2/(a+a)}Vp(h) = πaVp(h) (B-8)
式(B-7)を上式に代入して、h = ∞ → h の範囲で積分すると、静電相互作用によるVRエネルギーとして、次式が得られる。
VR(h) = 64πankTγ2/κ2 exp(-κh) (B-9)
式(B-10)についても同様に計算するか、または、PR(h) = – dVR(h)/dhからも求められる。
PR(h) = 64πankTγ2/κ exp(-κh) (B-10)
解説(A)の式(A-5)において、zeΨo/(4kT)≦1のとき、γ = tanh[zeΨo/(4kT)] ≒ zeΨo/(4kT)となり、この近似したγと式(Ⅰ-9)で示すκを上記の式(B-9)・(B-10)にそれぞれ代入すると、次の近似式が得られる。
PR(h) = 2πaεκΨo2 exp(-κh) (B-11)
VR(h) = 2πaεΨo2 exp(-κh) (B-12)
1.3 本モデル以外のコロイド系
<厚い二重層または小粒子系:a<1/κ >
VR(h) = 4πεΨo2a2/(h + 2a)・exp(-κh) (B-13)
<広範囲のκaへ適用可能な式>
VR(h) = 4πεΨo2a(h + a)/(h + 2a)・ln[1 + a/(h + a)・exp(-κh)] (B-14)
式(B-14)は、近距離 h≪aでは、a≫1/κの式(B-12)になる一方、遠距離 h≫aではa<1/κの式(B-13)に収束するので、広範囲のκaに適用可能と考えられている。
2.粒子間のvan der Waals相互作用
Hamker(1937)は、2枚の平行板および球形粒子間に働く引力のポテンシャルエネルギーVAを計算した。球形粒子間については、次式で示した。
VA = – (A/6){2/(S2 – 4) + 2/S2 + ln(s2-4)/s2} (B-15)
ここで、s = 2a + h、a:粒子半径[m]、h:粒子の最短表面間距離[m] である。a≫hの場合には、次式で近似される。
VA = – aA/(12h) (B-16)
なお、2粒子間の引力PAは、式(A-16)を微分して次式で示される。
PA = aA/(12h2) (B-17)
解説(C) 界面電荷の発生
ところが、固体と液体の界面は様々な原因により、正または負に荷電している。そこで、界面電荷と反対符号の対イオンは、この電荷に引き付けられそのイオン数が増加している。しかし、この正・負のイオンが不均等領域は数十nmオーダーのミクロ的なものであり、マクロ的に見ると電気的中性を保っている。この正・負イオン数の不均等をもたらす原因は固体および液体中の電解質の組合せによって、様々に異なる。以下に、界面電荷が発生する代表的な事例について記載する。
<難溶性イオン結晶>
例えば、AgNO3とKI の溶液を混合してAgI 粒子のコロイド溶液を生成させるとき、KI を過剰に加えると、I–が粒子表面に付着して負の電荷を与える。AgNO3を過剰にすると、Ag+が付着して粒子は正の電荷をもつ。Ag+とI–はAgI 粒子に対する電位決定イオンである。
この事例では、K+やNO3–は、AgI 結晶と反応しない無関係イオンである。Ag+とI–の濃度が等しいとき、粒子表面の電荷は’0’となり、この状態を電荷ゼロ点(ZPC、zero-point of charge)という。このように電位決定イオンを持つ粒子では、その界面電荷を電位決定イオンの添加によって、正負いずれにも自由に制御することができる。
<水酸化物・酸化物>
代表的な酸化物表面の等電点については、前章Ⅰの表Ⅰ-4に示した。
<表面解離基>
タンパク質は-COOHおよび-NH2を有しており、低いpHで正に帯電(-NH3+)し、あるpHoで等電点を示し、さらにより高いpHで負に帯電(-COO–)する両性物質である。繊維の中で、絹やナイロンはタンパク質系であるので、両性で等電点pHoを有するが、それらの構造によってpHoは異なる値を示す。
<H+またはOH–の優先付着>
<吸着性イオン>
解説(D) 電解質効果とSchulze-Hardy法則
1.電解質効果
(ⅰ)無関係塩
(ⅱ)界面活性剤イオン
事例として、AgNO3を加えて正に帯電したAgI ゾルに、陰イオン性界而活性剤(アルキル硫酸ナトリウム CnH2n+1OSO3Na)を添加したときのζ-電位の変化、それに対応するW(後述する分散系の安定度定比)の変化を、それぞれ図D-1と図D-2に示す。陰イオン性活性剤の増加とともにζ-電位は低下し、ζ-電位が’0’となる濃度Coを超えるとζ-電位は負の値を示すようになる。活性剤濃度が Coでは、AgI コロイドは急速凝集することとなる。図D-2に示すように、反対符号イオンの界面活性剤の添加によって凝集作用を示すが、添加量がCoを超えると逆に分散作用を示すこととなる。炭素数 nが大きくなるほど、疎水性コロイドへの吸着力が強くなるので、低濃度のCoを示している。
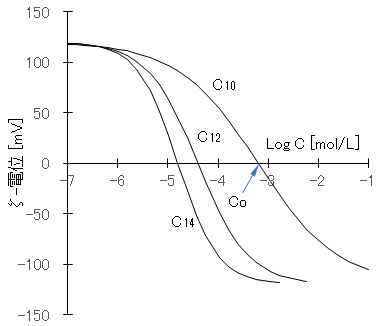
図D-1 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度とζ-電位の関係
測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。
ζ = ζo tanh[(X – b)/a]、X = log x
ζo:120[mV]、x:添加濃度C[mol/L]、C10:a = 1.6;b = -3.2、C12:a = 1.0;b = -4.4、C14:a = 0.8;b = -4.8
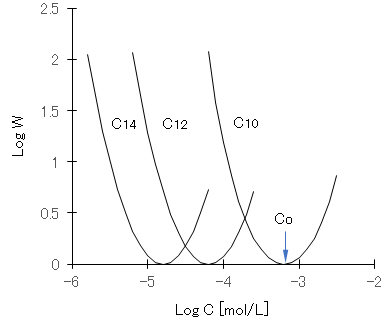
図D-2 AgIの陽性ゾルにアルキル硫酸ナトリウムの添加濃度と安定度比(W)の関係
測定値(Otterwill & Watanabe, 1960)を次式でフィッティングした。
Log W = c {cosh[a(X – b) – 1}、X = log x
C10:a = 2.0;b = -3.2;c = 0.8、C12:a = 1.0;b = -4.2;c = 3.8、C14:a = 0.5;b = -4.8;c = 16
(ⅲ)有機イオン、錯イオン
(ⅳ)電位決定イオン
2.Schulze-Hardyの原子価法則
疎水コロイドに電解質を加えるとき、その濃度がある値以上になると急速に凝集が起きる。この最低濃度を臨界凝集濃度(cfc)または単に凝集濃度という。凝集濃度は測定法で異なるが、精度のよいのは、次項で述べる安定度比Wの電解質濃度変化を求める方法である。この方法で得られた代表的なデータを表D-1に示す。
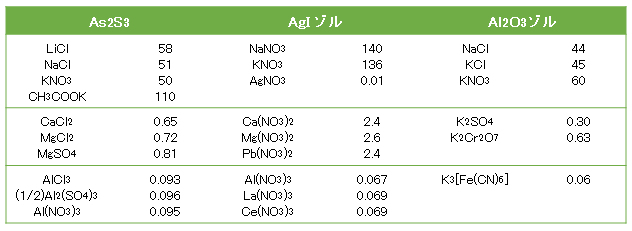
例外は吸着性の大きい有機イオンを含む電解質(CH3COOK)と、同じく吸着性の大きいイオンを含む電解質AgNO3(Ag+が電位決定イオン)の場合である。前項のDLVO理論では粒子の相互作用に際して表面電位Ψoは変化しないとしている。すなわち、この法則では非吸着性の電解質が対象である。
次のようにして、DLVO理論からSchulze-Hardy法則を導くことができる。
今、図Ⅰ-6に示す粒子の分散・凝集の分岐点をVmax = 0とすると、その極大値においては dV/dh = 0である。ここで、VRとして式(B-9)を、VAとして式(B-16)を式(Ⅰ-5)に代入し、V = 0 およびdV/dh = 0、という条件から、次式が得られる。
Cf = αε3T5γ4/(A2z6) ∝ 1/z6 (C-1)
α:定数、Cf:モル濃度で表したcfc
上式から、cfc は 1/z6に比例しており、DLVO理論からもSchulze-Hardyの原子価法則が説明できる。
解説(E) コロイドの凝集速度
コロイド系の安定性については、Ⅰ-3および解説(B)で述べた。しかし、コロイド系は永久的に持続するものではなくて、凝集するには高い壁があって、その壁を越える速度が遅いのである。ここでは、コロイドの凝集速度について、簡単に説明する。
凝集が、2粒子の衝突で起こる。凝集した2粒子1個と考え、凝集粒子は再分散しない不可逆系とする。一定体積中の粒子数をNとすると、凝集速度は次式で示される。
– dN/dt = kcN2 (E-1)
kcを凝集速度定数という。初期粒子数をNoとすると、上式を積分すると、
1/N – 1/No = kct (E-2)
<急速凝集の速度>
急速凝集のときの速度定数をkocとおくと、Smoluchowskiの拡散律速の理論より、
koc = 8πDa (E-3)
ここで、Dは粒子の拡散係数、aは粒子半径である。Dについて、Einstain-Stokesの式
D = kT/(6πηa) (Ⅰ-15)
を式(E-3)に代入すると、
koc = 4kT/(3η) (E-4)
が得られる。また、式(E-2)において、半減期 t = t1/2、N = No/2を代入すると、
t1/2 = 1/(kocNo) = 3η/(4kTNo) (E-5)
上式が示すように、急速凝集の速度定数は拡散律速であるので、温度Tと媒質の粘度ηのみで決まってしまう。25℃の水中において、No = 6×1016個/m3の時、半減期は2.8秒と計算される。
凝集が、2粒子の衝突で起こる。凝集した2粒子1個と考え、凝集粒子は再分散しない不可逆系とする。一定体積中の粒子数をNとすると、凝集速度は次式で示される。
kcを凝集速度定数という。初期粒子数をNoとすると、上式を積分すると、
ここで、Dは粒子の拡散係数、aは粒子半径である。Dについて、Einstain-Stokesの式
を式(E-3)に代入すると、
が得られる。また、式(E-2)において、半減期 t = t1/2、N = No/2を代入すると、
上式が示すように、急速凝集の速度定数は拡散律速であるので、温度Tと媒質の粘度ηのみで決まってしまう。25℃の水中において、No = 6×1016個/m3の時、半減期は2.8秒と計算される。
<緩慢凝集>
というWを定義し、これを分散系の安定度比と名付けている。Wは、その値が大きいほど凝集は遅く安定性がよいこととなり、分散・凝集の定量的尺度となる。W値は実験的にkocとkcの値を求めることによっても得られる。たとえば、粒子数またはそれに対応する物性(濁り度)を時間的に追跡して、kocとkcの値を求める。
また、Reerink-Overbeekによる次の関係からWを計算することができる。
2κa ≒ 1とすると、Vmaxが増すと指数関数的にWは増加する。Ⅰ-3.1 の<疎水コロイドの凝集と分散>で述べたように、Vmaxが一桁くらいでは分散系は不安定である。溶媒の粘度・温度などの条件にもよるが、Vmax>15kTになるとかなり分散性がよいこととなる。
たとえば、Noを一定とすると、t1/2は kcに逆比例することから、急速凝集の半減期を to1/2とすると、W = t1/2/to1/2となる。今、to1/2 = 1 [s]、2κa = 1として、Vmax = 15kTを式(E-7)に代入すると、t1/2 = exp(15) [s] = 38 [日]となる。
参考文献
Alonso, M. and E. J. Finn, E.J.: University Physics-Volume Ⅱ Field and Waves, Addison-Wesley Publoshing Co., 1967
Bergdtrom, L.: Hamaker Constants of Inorganic Materials, Advances in Colloid and Interface Science, 70, pp.125-169, 1997
Derjaguin, B.V.: Kolloid Z. (in German). Vol.69, No.2, pp.155–164, 1934
Hamaker, H.C.: Physica Ⅳ, No.10, 1058, 1937
Otterwill, R.H. & A. Watanabe: Kolloid. Z., Vol.170, p.133, Fig.1, p.135, Fig.4(1960)
池上 徹(栗田工業KCRセンター):水処理教室-凝集処理、https://kcr.kurita.co.jp/wtschool/012.html
化学工学協会編:化学工学便覧、丸善、1978
北原 文雄・渡辺 晶:界面電気現象-基礎・測定・応用-、共立出版、1972
北原 文雄:界面・コロイド化学の基礎、講談社、1994
作花 済夫:ゾル-ゲル法の科学、アグネ承風社、1988
小林 幹雄・他4名共編:数学公式集:共立出版、2005
長谷川 裕也:コロイド化学、http://sekatsu-kagaku.sub.jp/colloid.htm
福田 清成・中垣 正幸:コロイド化学の基礎、大日本図書、1969
粉体工学会編:液相中の粒子分散・凝集と分離操作、日刊工業新聞社、2010
松村 淳司:界面・電気化学講義、http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf
用水廃水便覧編集委員会編:用水・廃水便覧、丸善、1973
目次へ
掲載日:2019年03月29日
更新日:2019日04月11日(計算値を訂正、図Ⅰ-15を更新)
