村上定瞭(水浄化フォーラム)
1.基礎知識
(1)基礎式
(2)活量と濃度
(3)電位-pH
(4)水の電位-pH
2.有機酸・無機酸の電位-pH
(1)キノン
(2)炭酸
3.金属の電位-pH
(1)アルミニウム
(2)鉄
4.電位-pHの計算・作図
(1)基礎式
(2)活量と濃度
(3)電位-pH
(4)水の電位-pH
2.有機酸・無機酸の電位-pH
(1)キノン
(2)炭酸
3.金属の電位-pH
(1)アルミニウム
(2)鉄
4.電位-pHの計算・作図
水には、様々な溶質が溶解し、また、気体・固体と接して、物理・化学・生物的な相互作用を受けている。水を扱う時、何を目的として水を扱うかによって、視点(指標)が異なる。
事例を挙げると、飲料水では、先ず、人体に安全であること、次に味がよい(美味しい)水であることが視点となり、その溶質の構成(その濃度を含む)はどのうようなものであるかが、飲料水の指標となる。農業では、植物の生長に必要な溶質と土壌との関係が指標となる。発電所では水は熱交換の媒体として利用され、熱交換器や配管の腐食が起こらないような溶質の構成が重要となる。
上記事例では、個々の目的により、その視点が異なるが、共通的な視点がある。例えば、溶解度、pH、電位、錯体などがあり、それらの条件によって、溶質の状態と構成が異なる。
本ページでは、水の電位とpHが、溶質(水と接触する固体を含む)に対してどのような影響を与えるかについて、基礎知識と具体的事例をあげて解説する。
なお、本サイトの訪問者の内、本ページ(掲載:2018年01月)へのアクセス割合は高い。自然水の動態、飲料水の味と安全、産業用水と排水、農業と土壌など、水の電位-pHの理解は、溶質動態の把握、適正な水質測定、あるいは効果的な処理プロセスの開発と適正な維持管理において、極めて重要であることを示している。また、訪問者からの要望もあり、今回、「4.電位-pHの計算・作図」について追加記載(更新:2019年09月)することとした。
事例を挙げると、飲料水では、先ず、人体に安全であること、次に味がよい(美味しい)水であることが視点となり、その溶質の構成(その濃度を含む)はどのうようなものであるかが、飲料水の指標となる。農業では、植物の生長に必要な溶質と土壌との関係が指標となる。発電所では水は熱交換の媒体として利用され、熱交換器や配管の腐食が起こらないような溶質の構成が重要となる。
上記事例では、個々の目的により、その視点が異なるが、共通的な視点がある。例えば、溶解度、pH、電位、錯体などがあり、それらの条件によって、溶質の状態と構成が異なる。
本ページでは、水の電位とpHが、溶質(水と接触する固体を含む)に対してどのような影響を与えるかについて、基礎知識と具体的事例をあげて解説する。
なお、本サイトの訪問者の内、本ページ(掲載:2018年01月)へのアクセス割合は高い。自然水の動態、飲料水の味と安全、産業用水と排水、農業と土壌など、水の電位-pHの理解は、溶質動態の把握、適正な水質測定、あるいは効果的な処理プロセスの開発と適正な維持管理において、極めて重要であることを示している。また、訪問者からの要望もあり、今回、「4.電位-pHの計算・作図」について追加記載(更新:2019年09月)することとした。
1.基礎知識
(1)基礎式
電位(e–)とpH(水素イオンH+)が関与する反応は、つぎの式で一般化できる。
aA + mH+ + ze– = bB + cH2O (1)
反応(1)における自由エネルギー変化ΔGを、各物質Xの化学ポテンシャルμXの和で示すと、
-ΔG = aμA + mμH – bμB – cμH2O (2)
物質Xの化学ポテンシャルμXとその活量aXの関係を示す。
μX = μ°X + RTln aX (3)
式(3)を用いて、式(2)を表す。
-ΔG = -ΔG°- RTln (aBb/(aAaaHm)) (4)
ここで、
-ΔG°= aμ°A + mμ°H – bμ°B – mμ°H2O – cRTln aH2O
とし、希薄水溶液系では水の活量は変化しないものとして、定数ΔG°に含めた。
一方、反応(1)では、電気量zFを伴い、その自由エネルギー変化ΔGは、
-ΔG = zFE → E = -ΔG/(zF) (5)
式(5)に式(4)を代入すると、E°= -ΔG°/(zF)として、次式を得る。
E = E°- RT/(zF) ln (aBb/aAa /aHm ) (6)
定数R、F、温度25℃、ln = 2.303log、pH = –log aHの関係から、式(6)を書き直す。
E = E°- 0.0591(m/z)pH + 0.0591(1/z)(alog aA – blog aB) (7)
aA + mH+ + ze– = bB + cH2O (1)
反応(1)における自由エネルギー変化ΔGを、各物質Xの化学ポテンシャルμXの和で示すと、
-ΔG = aμA + mμH – bμB – cμH2O (2)
物質Xの化学ポテンシャルμXとその活量aXの関係を示す。
μX = μ°X + RTln aX (3)
式(3)を用いて、式(2)を表す。
-ΔG = -ΔG°- RTln (aBb/(aAaaHm)) (4)
ここで、
-ΔG°= aμ°A + mμ°H – bμ°B – mμ°H2O – cRTln aH2O
とし、希薄水溶液系では水の活量は変化しないものとして、定数ΔG°に含めた。
一方、反応(1)では、電気量zFを伴い、その自由エネルギー変化ΔGは、
-ΔG = zFE → E = -ΔG/(zF) (5)
式(5)に式(4)を代入すると、E°= -ΔG°/(zF)として、次式を得る。
E = E°- RT/(zF) ln (aBb/aAa /aHm ) (6)
定数R、F、温度25℃、ln = 2.303log、pH = –log aHの関係から、式(6)を書き直す。
E = E°- 0.0591(m/z)pH + 0.0591(1/z)(alog aA – blog aB) (7)
(2)活量と濃度
物理化学の分野においては溶質は活量で示すが、具体的な水浄化の分野では溶質は濃度で示すほうが便利である。
式(3)で示す溶質Xの活量aXは、その活量係数fxおよび濃度[X]でつぎのように示される。
aX= fX[X] (8)
希薄水溶液では、一般的に活量係数fXは’1’で近似できるので、
aX = [X] (9)
平衡反応式(1)に対して、式(7)はつぎのように示すことができる。
E = E°- 0.0591(m/z)pH + 0.0591(1/z)(alog[A] – blog[B])
= E°- 0.0591(m/z)pH – 0.0591(1/z)(apA – bpB) (7′)
留意事項
なお、本ページでは、簡略表記のため、pX = –log[X]、を多様するので留意されたい。
式(3)で示す溶質Xの活量aXは、その活量係数fxおよび濃度[X]でつぎのように示される。
aX= fX[X] (8)
希薄水溶液では、一般的に活量係数fXは’1’で近似できるので、
aX = [X] (9)
平衡反応式(1)に対して、式(7)はつぎのように示すことができる。
E = E°- 0.0591(m/z)pH + 0.0591(1/z)(alog[A] – blog[B])
= E°- 0.0591(m/z)pH – 0.0591(1/z)(apA – bpB) (7′)
留意事項
なお、本ページでは、簡略表記のため、pX = –log[X]、を多様するので留意されたい。
(3)電位-pH
① m = 0 のときの平衡図
式(1)および式(7)は、
aA + ze- = bB + cH2O (1a)
E = E°- 0.0591(1/z)(apA – bpB) (7a)
となり、Eだけに関係し、pHには無関係となるので、電位-pH平衡図はpH軸に平行な直線となる。
② z = 0 ときの平衡図
式(1)は、つぎのようになる。
aA + mH+ = bB + cH2O (1b)
反応(1b)の平衡定数Kとすると、式(8)が得られる。
K = [B]b/([A]a[H+]m)
apA – bpB = – pK – mpH (8)
この化学反応の平衡条件はpHのみに関係し、電位に無関係であるので、E軸に平行な直線となる。
式(1)および式(7)は、
aA + ze- = bB + cH2O (1a)
E = E°- 0.0591(1/z)(apA – bpB) (7a)
となり、Eだけに関係し、pHには無関係となるので、電位-pH平衡図はpH軸に平行な直線となる。
② z = 0 ときの平衡図
式(1)は、つぎのようになる。
aA + mH+ = bB + cH2O (1b)
反応(1b)の平衡定数Kとすると、式(8)が得られる。
K = [B]b/([A]a[H+]m)
apA – bpB = – pK – mpH (8)
この化学反応の平衡条件はpHのみに関係し、電位に無関係であるので、E軸に平行な直線となる。
(4)水の電位-pH
水が分解して酸素ガスと水素ガスになる反応は、
2H2O = O2 + 4H+ + 4e– (9)
2H+ + 2e– = H2 (10)
気体Xの分圧をPXで表記し、上記の反応を式(7)で示すと、
E = 1.228 – 0.0591pH – 0.0148pPO2 (11)
E = -0.0591pH + 0.0295pPH2 (12)
今、pPXに対して0、1、2、・・・に対するE-pHの平衡図を図1に示す。
この図について、若干の説明をする。水に一対のPt電極を浸漬し、両電極に加電(直流)し次第にその電圧を増していくと、陽極Ptでは酸素が発生して溶解し、陰極Ptでは水素が発生して溶解する。さらに、電圧を増加して、酸素および水素の分圧が大気圧(1atm)に達すると、それぞれの電極上からガス泡の発生が観測されるようになる。図中の赤線および緑線は、各pHにおける発生する酸素および水素の分圧と電位の関係を示している。pPXは分圧の逆対数を示しているので、図中に示すそれぞれの数値0、4、8、12は、1、10-4、10-8、10-12気圧に対応する電位とpHの関係を示している。
<注意事項>
実際の電気化学反応は過電圧(速度抵抗や液抵抗)などの因子が関係し、E-pH 平衡図と実験事実とは多々異なることに注意する。例えば、水の実際の分解電圧は、両極における過電圧により、1.7~1.8Vを示す。E-pHの平衡図に限らず、平衡反応と実際の反応(実験では、速度を伴う時間の因子を含む)が一致しないことは矛盾することではない。現実に起こる反応を予測・推定する上で、平衡反応が重要であることに変わりはない。
2H2O = O2 + 4H+ + 4e– (9)
2H+ + 2e– = H2 (10)
気体Xの分圧をPXで表記し、上記の反応を式(7)で示すと、
E = 1.228 – 0.0591pH – 0.0148pPO2 (11)
E = -0.0591pH + 0.0295pPH2 (12)
今、pPXに対して0、1、2、・・・に対するE-pHの平衡図を図1に示す。
この図について、若干の説明をする。水に一対のPt電極を浸漬し、両電極に加電(直流)し次第にその電圧を増していくと、陽極Ptでは酸素が発生して溶解し、陰極Ptでは水素が発生して溶解する。さらに、電圧を増加して、酸素および水素の分圧が大気圧(1atm)に達すると、それぞれの電極上からガス泡の発生が観測されるようになる。図中の赤線および緑線は、各pHにおける発生する酸素および水素の分圧と電位の関係を示している。pPXは分圧の逆対数を示しているので、図中に示すそれぞれの数値0、4、8、12は、1、10-4、10-8、10-12気圧に対応する電位とpHの関係を示している。
<注意事項>
実際の電気化学反応は過電圧(速度抵抗や液抵抗)などの因子が関係し、E-pH 平衡図と実験事実とは多々異なることに注意する。例えば、水の実際の分解電圧は、両極における過電圧により、1.7~1.8Vを示す。E-pHの平衡図に限らず、平衡反応と実際の反応(実験では、速度を伴う時間の因子を含む)が一致しないことは矛盾することではない。現実に起こる反応を予測・推定する上で、平衡反応が重要であることに変わりはない。
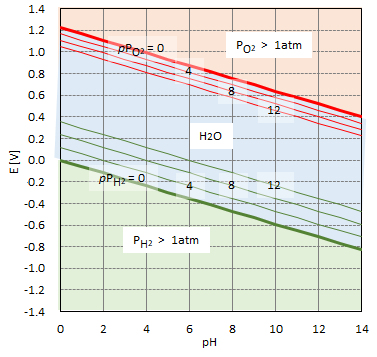
図1 水の電位-pH 平衡図
目次へ
2.有機酸・無機酸の電位-pH
(1)キノン
水中に溶存する不飽和脂肪酸は安定で、生体内の酵素や強い化学条件下でのみ酸化還元されるが、水の電気分解の範囲内の酸化還元電位での変化は起こらない。
ベンゼン骨格に酸素や窒素が結合した有機化合物では、その置換基の酸化還元反応が容易に生じる。図1で示したように、大気圧(1atm)において水が酸化還元分解しない電位内で、酸化還元反応を示す有機酸の代表例として、キノンQとヒドロキノンH2Qの酸化還元電位を事例として挙げる。なお、ここでは概略を理解することが目的であり、取扱を簡略するため、希薄水溶液とし各物質の活量係数は全て‘1’とし、濃度表示で記載する。
Q + 2H+ 2e– = H2Q E = Eº+ RT/(2F) ln K (1q)
一方、ヒドロキノンはつぎのように酸解離する。
H2Q = HQ– + H+ Ka2 = [HQ–][H+]/[H2Q] (2q)
HQ– = Q2- +H+ Ka1 = [Q2-][H+]/[HQ–] (3q)
文献値によって解離定数の値が異なる(測定条件の相違)が、ここでは、Eº= 0.70V、pKa1=11.5、pKa2=9.9を用いいる。
ヒドロキノンの解離種について、pH-存在率の関係を図2に示す。pH<pKa1では、H2Qが、pKa2<pH<pKa1ではHQ–が、pKa1<pHではQ2-が、それぞれ主たる解離種である。
上記式(7’)を式(1q)に当てはめると
E = 0.70 – 0.0591pH – 0.0296(pQ – pH2Q) (4q)
式(2q)より得た、pH2Q = pHQ– + pH – pKa2 、を式(4q)に代入して、
E = 0.41– 0.0296pH – 0.0296(pQ – pHQ–) (5q)
式(3q)より得た、 pHQ– = pQ2- + pH – pKa1 、を式(5q)に代入して、
E = 0.070 – 0.0296(pQ – pQ2-) (6q)
ここで、式(4q)~(6q)において、それぞれ、[Q]=[H2Q]、[Q]=[HQ–]、[Q]=[Q2-]の条件では、各式の最後の項は’0’となる。この条件下でE-pHの関係をグラフ化したものが、図3である。
すなわち、式(4q)→AB、式(5q)→BC、式(6q)→CDにそれぞれ対応するE-pHのグラフで、CDはpHに依存せずEは一定で、pHに平行な直線となる。
ベンゼン骨格に酸素や窒素が結合した有機化合物では、その置換基の酸化還元反応が容易に生じる。図1で示したように、大気圧(1atm)において水が酸化還元分解しない電位内で、酸化還元反応を示す有機酸の代表例として、キノンQとヒドロキノンH2Qの酸化還元電位を事例として挙げる。なお、ここでは概略を理解することが目的であり、取扱を簡略するため、希薄水溶液とし各物質の活量係数は全て‘1’とし、濃度表示で記載する。
Q + 2H+ 2e– = H2Q E = Eº+ RT/(2F) ln K (1q)
一方、ヒドロキノンはつぎのように酸解離する。
H2Q = HQ– + H+ Ka2 = [HQ–][H+]/[H2Q] (2q)
HQ– = Q2- +H+ Ka1 = [Q2-][H+]/[HQ–] (3q)
文献値によって解離定数の値が異なる(測定条件の相違)が、ここでは、Eº= 0.70V、pKa1=11.5、pKa2=9.9を用いいる。
ヒドロキノンの解離種について、pH-存在率の関係を図2に示す。pH<pKa1では、H2Qが、pKa2<pH<pKa1ではHQ–が、pKa1<pHではQ2-が、それぞれ主たる解離種である。
上記式(7’)を式(1q)に当てはめると
E = 0.70 – 0.0591pH – 0.0296(pQ – pH2Q) (4q)
式(2q)より得た、pH2Q = pHQ– + pH – pKa2 、を式(4q)に代入して、
E = 0.41– 0.0296pH – 0.0296(pQ – pHQ–) (5q)
式(3q)より得た、 pHQ– = pQ2- + pH – pKa1 、を式(5q)に代入して、
E = 0.070 – 0.0296(pQ – pQ2-) (6q)
ここで、式(4q)~(6q)において、それぞれ、[Q]=[H2Q]、[Q]=[HQ–]、[Q]=[Q2-]の条件では、各式の最後の項は’0’となる。この条件下でE-pHの関係をグラフ化したものが、図3である。
すなわち、式(4q)→AB、式(5q)→BC、式(6q)→CDにそれぞれ対応するE-pHのグラフで、CDはpHに依存せずEは一定で、pHに平行な直線となる。
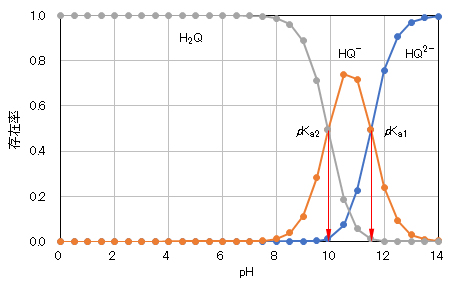
図2 ヒドロキノンの解離種のpH-存在率の関係
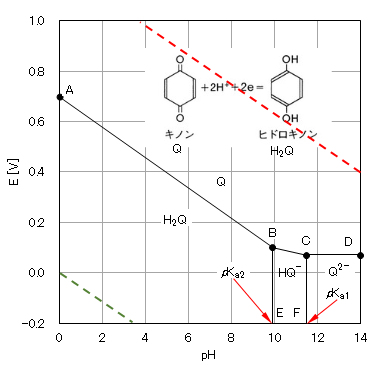
図3 キノン-ヒドロキノンの電位-pH 平衡図(25℃、1atm)
黒線AB:Q-H2Q、黒線BC:Q-HQ–、黒線CD:Q-Q2-、緑点線:H2発生(1atm)、赤点線:O2発生(1atm)
(2)炭酸
アルカリ・アルカリ土類金属イオンNa+やMg2+が存在する水溶液では、水溶液の電気的中性を保つため、炭酸イオンが水に溶解し、環境水(地表水・地下水・海水)のpHを安定に保っている。また、微生物・植物による光合成やメタン発酵(好気条件下での炭素循環)などにより、大気圏・水圏・土壌/底泥圏での炭素循環が行われている。しかし、通常の水の化学条件下では酸化還元は生じない。図4に炭酸の化学形態種と電位-pHの関係を示す。
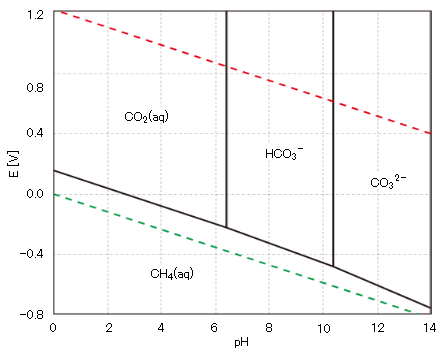
図4 炭酸H2CO3の希薄水溶液の電位-pH 平衡図
pΣ[Ci]=10、25℃、1atm
目次へ
3.金属の電位-pH
(1)アルミニウム
溶融(約1,000℃)した氷晶石Na2AlOF3にAl2O3を加えて電気分解して純粋なAlを得ることができる。しかし、水中でのアルミニウムはAl(Ⅲ)が安定で酸化還元反応は生じない。したがって、希薄水溶液中での化学形態種と電位-pHの関係は図5にようになる。詳しくは、別ページを参照されたい。
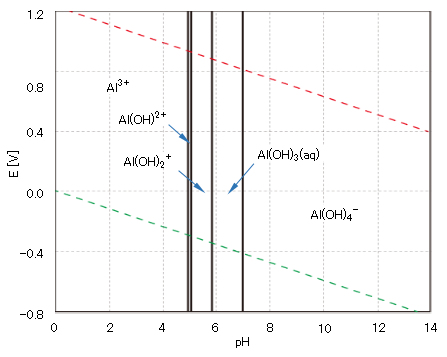
図5 アルミニウムAlの希薄水溶液の電位-pH 平衡図
pΣ[Ali]=10、25℃、1atm
(2)鉄
鉄は遷移金属で、水中ではpHおよび酸化還元電位により様々な化学形態として存在する。図6に希薄水溶液中での鉄の化学形態種と電位-pHの関係を示す。詳しくは、別ページを参照されたい。
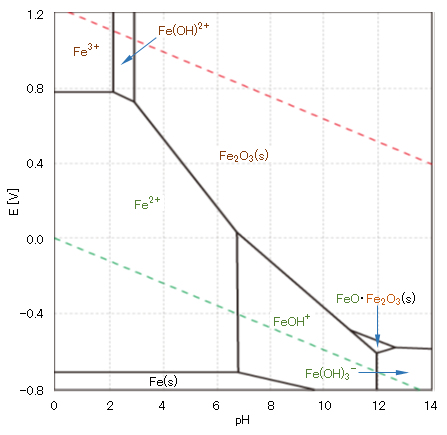
図6 鉄Feの希薄水溶液の電位-pH 平衡図
物質記号(鉄の酸化数)の色:黒-金属Fe、緑-Fe2+、茶-Fe3+;pΣ[Fei]=10、25℃、1atm
目次へ
4.電位-pHの計算・作図
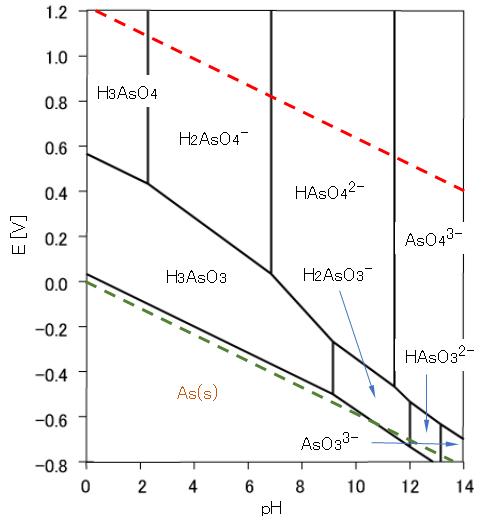
ひ素Asを事例として、その電位-pHの平衡図の作成について、説明する。
Asは自然界では、硫化物・酸化物・金属ひ化物として岩石・土壌・環境水中に広く存在し、ほとんどすべの生物体中にも有機ひ素化合物として微量に存在している。
有害性物質で、環境基準0.01mg/L以下、排水基準0.1mg/L以下に規定されている。
Asは、通常、As(-Ⅲ)、As(0)、As(Ⅲ)、As(Ⅴ)の酸化数の化合物が存在するが、H3As(-Ⅲ)は揮発性で、魚類中に多量に含まれるアルセノペンイン (CH3)3As+CH2COOH(-Ⅲ)はほとんど毒性がない。ジメチルアルシン酸 CH3AsOOH(-Ⅳ)は発がん性があるといわれる。As2O3(Ⅲ)は猛毒で、水に溶解して亜ヒ酸 H3AsO3となる。As2O5(Ⅴ)も毒性であるが、As(Ⅲ)よりも弱い、水に溶解してヒ酸 H3AsO4となる。。
本ページでは、環境水(海水・地下水・河川・湖沼など)に含まれるひ酸 H3SO4(Ⅴ)、亜ヒ酸 H3AsO3(Ⅲ)およびコロイド As(s)の希薄水溶液について、電位-pHの平衡図の計算・作成の手順について説明する。
<注意>
計算・作図を具体的に行うExcel-ファイルを本サイトのサーバーに保存してあるので、学生・初心者はダウンロードして比較しながら、下記の計算・作図の手順を理解されたい。また、As以外の元素については、同ファイルを修正・加筆などして活用されたい。
Asは自然界では、硫化物・酸化物・金属ひ化物として岩石・土壌・環境水中に広く存在し、ほとんどすべの生物体中にも有機ひ素化合物として微量に存在している。
有害性物質で、環境基準0.01mg/L以下、排水基準0.1mg/L以下に規定されている。
Asは、通常、As(-Ⅲ)、As(0)、As(Ⅲ)、As(Ⅴ)の酸化数の化合物が存在するが、H3As(-Ⅲ)は揮発性で、魚類中に多量に含まれるアルセノペンイン (CH3)3As+CH2COOH(-Ⅲ)はほとんど毒性がない。ジメチルアルシン酸 CH3AsOOH(-Ⅳ)は発がん性があるといわれる。As2O3(Ⅲ)は猛毒で、水に溶解して亜ヒ酸 H3AsO3となる。As2O5(Ⅴ)も毒性であるが、As(Ⅲ)よりも弱い、水に溶解してヒ酸 H3AsO4となる。。
本ページでは、環境水(海水・地下水・河川・湖沼など)に含まれるひ酸 H3SO4(Ⅴ)、亜ヒ酸 H3AsO3(Ⅲ)およびコロイド As(s)の希薄水溶液について、電位-pHの平衡図の計算・作成の手順について説明する。
<注意>
計算・作図を具体的に行うExcel-ファイルを本サイトのサーバーに保存してあるので、学生・初心者はダウンロードして比較しながら、下記の計算・作図の手順を理解されたい。また、As以外の元素については、同ファイルを修正・加筆などして活用されたい。
(1)計算に必要な平衡定数
E-pH計算に必要な平衡反応およびそれらの定数を下記に列挙し、pK値の小さいものから順に式番号を付記する。
a) As(Ⅴ)とAs(Ⅲ)の酸解離定数
H3AsO4 ⇄ H+ + H2AsO4– pK3(Ⅴ) = 2.2 (a1)
H2AsO4– ⇄ H+ + H2AsO42- pK2(Ⅴ) = 6.9 (a2)
HAsO42- ⇄ H+ + H2AsO43- pK1(Ⅴ) = 11.5 (a4)
H3AsO3 ⇄ H+ + H2AsO3– pK3(Ⅲ) = 9.2 (a3)
H2AsO3– ⇄ H+ + HAsO32- pK2(Ⅲ) = 12.1 (a5)
HAsO32- ⇄ H+ + AsO3– pK1(Ⅲ) = 13.4 (a6)
b) As(Ⅴ)/As(Ⅲ)とAs(Ⅲ)/As(s)の酸化還元電位
H3AsO4 + 2H+ + 2e– ⇄ H3AsO3 Eo = 0.56V
H3AsO3 + 3H+ + 3e– ⇄ As(s) Eo =0.04V
H3AsO4 ⇄ H+ + H2AsO4– pK3(Ⅴ) = 2.2 (a1)
H2AsO4– ⇄ H+ + H2AsO42- pK2(Ⅴ) = 6.9 (a2)
HAsO42- ⇄ H+ + H2AsO43- pK1(Ⅴ) = 11.5 (a4)
H3AsO3 ⇄ H+ + H2AsO3– pK3(Ⅲ) = 9.2 (a3)
H2AsO3– ⇄ H+ + HAsO32- pK2(Ⅲ) = 12.1 (a5)
HAsO32- ⇄ H+ + AsO3– pK1(Ⅲ) = 13.4 (a6)
b) As(Ⅴ)/As(Ⅲ)とAs(Ⅲ)/As(s)の酸化還元電位
H3AsO4 + 2H+ + 2e– ⇄ H3AsO3 Eo = 0.56V
H3AsO3 + 3H+ + 3e– ⇄ As(s) Eo =0.04V
(2)平衡反応・定数のグラフ化と計算
a) 酸解離種と平衡定数のグラフ化

図7 As(Ⅴ)/As(Ⅲ)系の酸解離種と酸化還元反応の関係図

図8 As(Ⅲ)/As(s)系の酸解離種と酸化還元反応の関係図
b) 酸化還元反応の分類表1 As(Ⅴ)/As(Ⅲ)系酸化還元のE-pHの計算
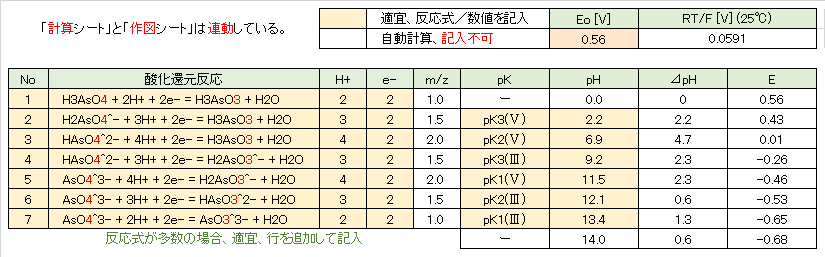
表2 As(Ⅲ)/As(s)系酸化還元のE-pHの計算
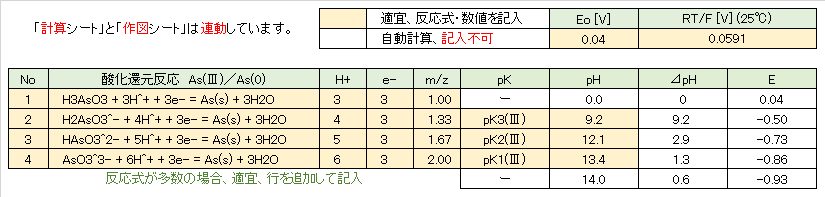
c) 電位-pHの計算表3 ひ素のE-pHの計算結果
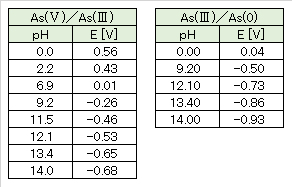
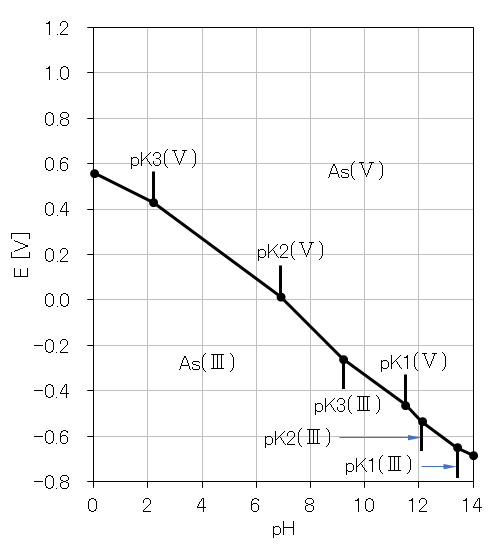
図9 As(Ⅴ)/As(Ⅲ)系のE-pH平衡図の作成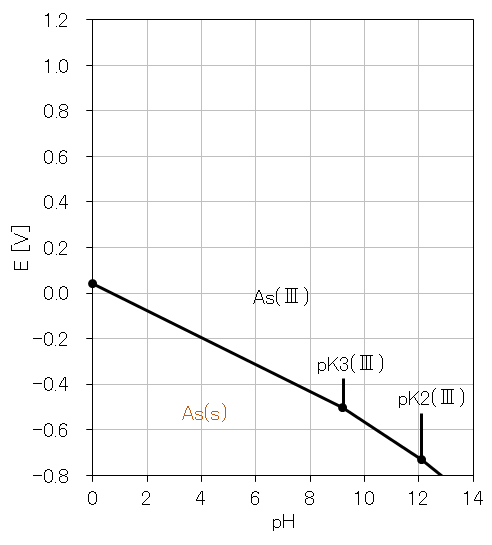
図10 As(Ⅲ)/As(s)系のE-pH平衡図の作成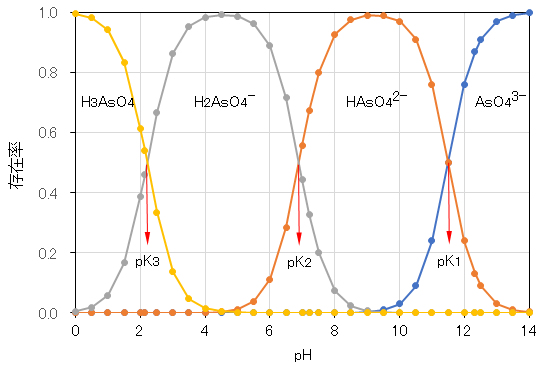
図12 ヒ酸 H3AsO4 のpH-存在率(計算・作図)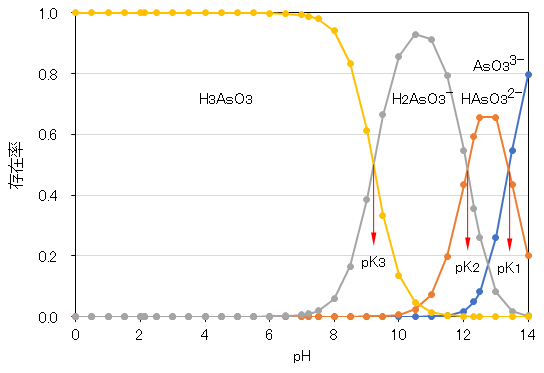
図13 亜ヒ酸 H3AsO3 のpH-存在率
掲載日:2018年01月23日
更新日:2019年09月04日(2章および3章の未記載部分を加筆)
更新日:2019年09月18日(4章を加筆)
As(Ⅴ)/As(Ⅲ)系およびAs(Ⅲ)/As(s)系について、それぞれ酸解離種と平衡定数の関係をpK値の小さいものから順に、図7および図8に示すようにグラフ化する。
なお、各pKi(Ⅴor Ⅲ)に対応するpHにおいて、[HiAsOx(3-i)-] = [Hi-1AsOx(4-i)-] (i = 1~3、x = 4 or 3)となる。
なお、各pKi(Ⅴor Ⅲ)に対応するpHにおいて、[HiAsOx(3-i)-] = [Hi-1AsOx(4-i)-] (i = 1~3、x = 4 or 3)となる。

図7 As(Ⅴ)/As(Ⅲ)系の酸解離種と酸化還元反応の関係図

図8 As(Ⅲ)/As(s)系の酸解離種と酸化還元反応の関係図
b) 酸化還元反応の分類
As(Ⅴ)/As(Ⅲ)系
図7を見ると分かるように、H3AsO4(Ⅲ)が存在する 0≦pH≦9.2 において、共存するAs(Ⅴ)の解離種はH3AsO4~HAsO42-の3つがあるので、表1のNo1~No3の酸化還元平衡が存在する。
同様に、H2AsO4–(Ⅲ)が存在する 9.2≦pH≦12.1 において、共存するAs(Ⅴ)の解離種はHAsO42-とAsO43-の2つがあるので、表1のNo4~No5の酸化還元反応が存在する。
HAsO42-(Ⅲ)およびAsO43-(Ⅲ)が存在するそれぞれのpH領域(12.1≦pH≦13.4、13.4≦pH≦14)において、共存するAs(Ⅴ)の解離種はAsO43-のみであるので、表1のNo6~No7の酸化還元反応が存在する。
As(Ⅲ)/As(s)系
図8を見ると分かるように、As(s)は 0≦pH≦14 において変化しないので、As(s)とAs(Ⅲ)の各解離種との組合せのみで、表2に示すNo1~No4の酸化還元反応が存在する。
図7を見ると分かるように、H3AsO4(Ⅲ)が存在する 0≦pH≦9.2 において、共存するAs(Ⅴ)の解離種はH3AsO4~HAsO42-の3つがあるので、表1のNo1~No3の酸化還元平衡が存在する。
同様に、H2AsO4–(Ⅲ)が存在する 9.2≦pH≦12.1 において、共存するAs(Ⅴ)の解離種はHAsO42-とAsO43-の2つがあるので、表1のNo4~No5の酸化還元反応が存在する。
HAsO42-(Ⅲ)およびAsO43-(Ⅲ)が存在するそれぞれのpH領域(12.1≦pH≦13.4、13.4≦pH≦14)において、共存するAs(Ⅴ)の解離種はAsO43-のみであるので、表1のNo6~No7の酸化還元反応が存在する。
As(Ⅲ)/As(s)系
図8を見ると分かるように、As(s)は 0≦pH≦14 において変化しないので、As(s)とAs(Ⅲ)の各解離種との組合せのみで、表2に示すNo1~No4の酸化還元反応が存在する。


c) 電位-pHの計算
As(Ⅴ)/As(Ⅲ)系
上記の1.基礎知識(1)基礎式に示す式(7)を用いて、図7に示すAs(Ⅴ)/As(Ⅲ)系の各pHにおける電位を計算する。本モデルでは希薄溶液であるので、(2)活量と濃度に示す式(7′)を用いることとする。
ここで、0≦pH≦2.2 の領域を計算するには式(7)の第二項の計算が必要となるが、簡略化して、このpH領域では、[H2AsO4–] = 0 として、[H3AsO4] = [H2AsO3] の条件では、式(7’)式は、次式のように簡単になる。
E1 = Eo-0.0591(m/z)ΔpH (As-1)
No1 の反応式から、Eo = 0.56V (pH 0.0)、m/Z = 1.0 であるので、ΔpH = 2.2 を式(As-1)に代入して、E1 = 0.43V (pH 2.2) を得る。
次に、2.2≦pH≦6.9 の領域では、 [H3AsO4] = [HAsO42-] = 0 として、[H2AsO4–] = [H3AsO3] の条件では、次式が成立する。
E2 = E1-0.0591(m/z)ΔpH (As-2)
No2 の反応式から、E1 = 0.43V、m/Z = 1.5であるので、ΔpH = 4.7 を式(As-2)に代入して、E2 = 0.01V (pH 6.9)を得る。
以下、順次、同様な計算を行うと、表7に示すような各pHに対する電位Eの数値が得られる。
As(Ⅲ)/As(s)系
この系の酸化還元反応は、図8に見られるように、0≦pH≦14の範囲でAs(s)のみが存在するので、As(Ⅴ)/As(Ⅲ)系に比べて、簡単である。表1について示した手順に沿って、計算すると、表2に示す結果が得られる。
上記の1.基礎知識(1)基礎式に示す式(7)を用いて、図7に示すAs(Ⅴ)/As(Ⅲ)系の各pHにおける電位を計算する。本モデルでは希薄溶液であるので、(2)活量と濃度に示す式(7′)を用いることとする。
ここで、0≦pH≦2.2 の領域を計算するには式(7)の第二項の計算が必要となるが、簡略化して、このpH領域では、[H2AsO4–] = 0 として、[H3AsO4] = [H2AsO3] の条件では、式(7’)式は、次式のように簡単になる。
No1 の反応式から、Eo = 0.56V (pH 0.0)、m/Z = 1.0 であるので、ΔpH = 2.2 を式(As-1)に代入して、E1 = 0.43V (pH 2.2) を得る。
次に、2.2≦pH≦6.9 の領域では、 [H3AsO4] = [HAsO42-] = 0 として、[H2AsO4–] = [H3AsO3] の条件では、次式が成立する。
No2 の反応式から、E1 = 0.43V、m/Z = 1.5であるので、ΔpH = 4.7 を式(As-2)に代入して、E2 = 0.01V (pH 6.9)を得る。
以下、順次、同様な計算を行うと、表7に示すような各pHに対する電位Eの数値が得られる。
As(Ⅲ)/As(s)系
この系の酸化還元反応は、図8に見られるように、0≦pH≦14の範囲でAs(s)のみが存在するので、As(Ⅴ)/As(Ⅲ)系に比べて、簡単である。表1について示した手順に沿って、計算すると、表2に示す結果が得られる。
As(Ⅴ)/As(Ⅲ)系およびAs(Ⅲ)/As(s)系の計算結果を表3にまとめて示す。これらの電位-pHをグラフ化したものを図9および図10に示す。
両図を重ね合わせる。次に、1.基礎知識(3)電位-pH ① Z = 0 のときの平衡図で述べたように、酸化解離反応では、pHのみに関係し、電位に無関係で、E軸に平行な直線となる。As(Ⅴ)およびAs(Ⅲ)の各解離種のpKi(図9および図10の各折線の交点)のpH軸を通ってE軸に平行な線を描くと、図11に示すひ素の希薄水溶液の電位-pH平行図が完成する。
両図を重ね合わせる。次に、1.基礎知識(3)電位-pH ① Z = 0 のときの平衡図で述べたように、酸化解離反応では、pHのみに関係し、電位に無関係で、E軸に平行な直線となる。As(Ⅴ)およびAs(Ⅲ)の各解離種のpKi(図9および図10の各折線の交点)のpH軸を通ってE軸に平行な線を描くと、図11に示すひ素の希薄水溶液の電位-pH平行図が完成する。


図9 As(Ⅴ)/As(Ⅲ)系のE-pH平衡図の作成

図10 As(Ⅲ)/As(s)系のE-pH平衡図の作成
a) ① 文献(書籍、解説論文、Webなど)に記載・表示されている電位-pH平衡図は、詳細に見ると様々に異なっていることが多い。前述したように、電位-pHの計算には、酸解離定数 Kiや標準酸化還元電位 Eoの値が必要であるが、引用する文献によって、Ki や Eo の値が異なっているからである。
この理由は、各定数(pKやEo)の測定条件や決定方法(留意事項)が異なるからである(関連する留意事項)。本サイト内でも、同じ定数がページによってその値が異なっていることもある。
② 次に、E-pH平衡図が、図11に示すような単線ではなく、図1に示すようなメイン線と多数のサブ線で描かれ、0、±2、±4、・・・などの添字が付記されている文献も多数ある。
本ページでは、E-pHの計算において、式(7′)の第二項を消去するため、次のようにモデル化を行っている。図7に示すpKi+1≦pH≦pKiの領域内では、HiAsOx(3-i)- (i = 0~2、x = 4 or 3)のみが存在することとしている。実際には、下記の図12および図13に示すように、pKi+1≦pH≦pKiの領域における主たる解離種であって、他の解離種も共存している。さらに、本ページでは全ての溶質を無限希釈(希薄溶液)としているが、上記リンク文献などでは水溶液中の各溶質の濃度(正確には活量)に対応するE-pHを式(7)を用いて計算・作図している(上記のメイン線は、平衡反応に関与する全ての対象溶質の活量が”1″の場合を示す)。しかしながら、平衡反応における各解離種の活量やpH-存在率の関係が分かるようになると、リンク文献に示された複雑なサブ線は、メイン線だけのE-pH平衡図(例えば、図11)を見れば、頭の中で描けるようになる。
学生や初心者にとって、このような状況は、必要なデータを検索し、具体的に計算・作図を行うことにより、深く理解できることである。本ページに限らず、自分で計算・作図を行うことが大切と考えている。
b) 自然水や排水には様々な溶解物質が共存し、それらの濃度も様々で、計算によって求めた本ページのE-pH平衡図(無限希釈、対象とする物質以外は存在しない条件)との間には、それらの条件に大きな差異がある。
また、実際のpH測定に当たって、ガラス電極などを利用する場合に、校正に使う標準液のpHを超える酸性・アルカリ性域では、その強さとともに直線性が外れてくる。
c) 本サイトの編集者の言いたいことは、”E-pH平衡図は自然水の状況、物質の定量測定、浄化プロセスの設計・維持管理などにおいて極めて有益な情報を提供するが、表示された値そのものには注意が必要で、具体的な適用にあたっては実験的な確認が必要である”ことである。
この理由は、各定数(pKやEo)の測定条件や決定方法(留意事項)が異なるからである(関連する留意事項)。本サイト内でも、同じ定数がページによってその値が異なっていることもある。
② 次に、E-pH平衡図が、図11に示すような単線ではなく、図1に示すようなメイン線と多数のサブ線で描かれ、0、±2、±4、・・・などの添字が付記されている文献も多数ある。
本ページでは、E-pHの計算において、式(7′)の第二項を消去するため、次のようにモデル化を行っている。図7に示すpKi+1≦pH≦pKiの領域内では、HiAsOx(3-i)- (i = 0~2、x = 4 or 3)のみが存在することとしている。実際には、下記の図12および図13に示すように、pKi+1≦pH≦pKiの領域における主たる解離種であって、他の解離種も共存している。さらに、本ページでは全ての溶質を無限希釈(希薄溶液)としているが、上記リンク文献などでは水溶液中の各溶質の濃度(正確には活量)に対応するE-pHを式(7)を用いて計算・作図している(上記のメイン線は、平衡反応に関与する全ての対象溶質の活量が”1″の場合を示す)。しかしながら、平衡反応における各解離種の活量やpH-存在率の関係が分かるようになると、リンク文献に示された複雑なサブ線は、メイン線だけのE-pH平衡図(例えば、図11)を見れば、頭の中で描けるようになる。
学生や初心者にとって、このような状況は、必要なデータを検索し、具体的に計算・作図を行うことにより、深く理解できることである。本ページに限らず、自分で計算・作図を行うことが大切と考えている。
b) 自然水や排水には様々な溶解物質が共存し、それらの濃度も様々で、計算によって求めた本ページのE-pH平衡図(無限希釈、対象とする物質以外は存在しない条件)との間には、それらの条件に大きな差異がある。
また、実際のpH測定に当たって、ガラス電極などを利用する場合に、校正に使う標準液のpHを超える酸性・アルカリ性域では、その強さとともに直線性が外れてくる。
c) 本サイトの編集者の言いたいことは、”E-pH平衡図は自然水の状況、物質の定量測定、浄化プロセスの設計・維持管理などにおいて極めて有益な情報を提供するが、表示された値そのものには注意が必要で、具体的な適用にあたっては実験的な確認が必要である”ことである。

図12 ヒ酸 H3AsO4 のpH-存在率(計算・作図)

図13 亜ヒ酸 H3AsO3 のpH-存在率
掲載日:2018年01月23日
更新日:2019年09月04日(2章および3章の未記載部分を加筆)
更新日:2019年09月18日(4章を加筆)