pH and solubility of metal ion
村上定瞭(水浄化フォーラム), Sadaaki Murakami (Water & Solutions Forum)
1. Introdauction
2. pH and solubility of metal ion
(1) Zinc(Ⅱ)
(2) Aluminum(Ⅲ)
3. Notes
4. Calculation
Apendix
1.はじめに
水分子は大きな極性を有し、電解質は水和して溶解する。イオン化傾向の高い金属(例えば、LiやNaなど)は水と常温で激しく反応してH2を発生し、陽イオンとなって水に溶解する。イオン化傾向がHより大きく中間に位置する金属(Al、Fe、Niなど)は希酸に溶けてH2を発生し、水に溶解する。Hよりもイオン化傾向が小さいCu、Ag、Auは酸化力の強い酸と反応して水に溶解するが、希酸とは反応しない。(詳細は別ページ参照)
ところで、溶解した陽イオンとpHとの関係を見ると、Li+、Na+,K+などの1価の金属イオンを除き、2価以上の金属イオンはpHが上昇すると、難溶性の水酸化物を生成する。
水に溶解した金属イオンは、水分子が配位した錯イオンを形成して安定化している(例えば、図1と図3)。pHが増加すると、配位した水分子がH+イオンを放出しOH–イオンとなる。さらに、逐次H+を放出して、金属イオンの価数と配位したOH–の数が等しくなると、式(1)に示すように、その金属錯体はその電荷が’ゼロ’となり水に難溶性となる。反応式(1)は、(1a)または(1b)のように簡略して表現される。
1. Introduction
Water molecules have a large polarity and the electrolyte hydrates and dissolves. A metal with a high ionization tendency (for example, Li or Na) reacts violently with water at room temperature to generate H2, which becomes a cation and dissolves in water. Metals with an ionization tendency higher than H and located in the middle (Al, Fe, Ni, etc.) dissolve in dilute acid to generate H2 and dissolve in water. Cu, Ag, and Au, which have a smaller ionization tendency than H, react with acids having strong oxidizing power and dissolve in water, but do not react with dilute acids. (See another page for details)
By the way, looking at the relationship between dissolved cations and pH , except for monovalent metal ions such as Li+, Na+, and K+, divalent or higher valent metal ions have poorly soluble hydroxides when the pH increases.
Metal ions dissolved in water form complex ions with water molecules coordinated and stabilized (for example, Figs.1 and 3). When the pH increases, the coordinated water molecules release H+ ion and become OH– ion. Furthermore, when H+ is sequentially released and the number of valences of the metal ion becomes equal to the number of coordinated OH–, the charge of the metal complex becomes ‘zero’ and it is considered to be sparingly soluble in water, as shown in equation (1). The formula (1) is simply expressed as (1a) or (1b).
Mm+ + mH2O → M(OH)m(s) + mH+ (1a)
Mm+ + mOH– → M(OH)m (s) (1b)
金属によっては、さらにpHが上昇してH+を放出すると、負の電荷を有する錯イオンとなり、再び水に溶解する。このような金属を両性水酸化物という。両性水酸化物を形成する代表的な金属イオンとしてAl3+、Zn2+、Pb2+などがある。
(n ≧ p > m) (2)
ここでは、代表的な両性物質であるアルミニウム(Ⅲ)および亜鉛(Ⅱ)を取り上げ、これらの金属イオンの溶解度とpHとの関係について紹介する。
なお、金属イオンに配位して錯イオン(または錯体)を形成するものや難溶性塩を形成するもの(電解質や非電解質を問わず)が共存する場合には、さらにその挙動が複雑となる。そこで、ここではそのような共存物質はないものとする。
Here, the representative amphoteric substances aluminum (III) and zinc (II) are taken up and the relationship between the solubility of these metal ions and pH is introduced.
When a complex ion (or complex) coordinating to a metal ion or a sparingly soluble salt (regardless of electrolyte or non-electrolyte) coexists, its behavior becomes more complicated. Therefore, it is assumed that there is no such coexisting substance here
注意事項1
過去において水中での金属イオンの配位構造が不明なこともあったので、式(2)に示す水分子を省略して、M(OH)p(p-m)-と表記したり、また、脱水した分子式で示すことが多い。たとえば、[Zn(H2O)(OH)3] –は、Zn(OH)3–またはZnO2H–のように表記されている。
Notes 1
In the past, the coordination structure of metal ions in water was unclear, so the water molecule shown in formula (2) was omitted and written as M(OH)p(p-m)-. Moreover, it is often shown by a dehydrated molecular formula. For example, [Zn(H2O)(OH)3] – is denoted as Zn(OH)3– or ZnO2H–.
2.pHと金属イオンの溶解度
(1)亜鉛(Ⅱ)
亜鉛(Ⅱ)の水和イオンの各解離種の構造を図1に示し、各解離種の簡略式を併せて示す(なお、図1に示す錯イオンはさらに分極した水分子層で囲まれている。)。この簡略を用いて、各解離種の平衡式およびそれぞれの平衡定数は以下のように示される。なお、平衡式は上記(1b)の表記法を用いている。Kbは式(1b)に対応し、Kaは式(1a)の左辺と右辺を逆にしたときの値を示している。
2. pH and solubility of metal ions
(1) Zinc (II)
The structure of each dissociated species of the hydrated ion of zinc (II) is shown in Fig. 1, and the simplified formula of each dissociated species is also shown (Note that the complex ion shown in Fig.1 is surrounded by a further polarized water molecules layer.). Using this simplification, the equilibrium equations for each dissociated species and their respective equilibrium constants are given below. The equilibrium equation uses the notation of (1b) above. Kb corresponds to the equation (1b), and Ka indicates a value when the left side and the right side of the equation (1a) are reversed.
ZnOH+ + OH– = Zn(OH)2(aq): pKb2 = -6.06, pKa2 = -7.94 (4)
Zn(OH)2(aq) + OH– = Zn(OH)3–: pKb3 = -2.50, pKa3 = -11.50 (5)
Zn(OH)3– + OH– = Zn(OH)42-: pKb4 = -1.20, pKa4 = -12.80 (6)
Zn2+ + 2OH– = Zn(OH)2(s): pKsp = 15.55 (7)
式(8)〜(13)の関係式を用いて、pH値と各解離種の濃度Cの関係を図2に示す。
図2に見られるように、亜鉛(Ⅱ)の溶解度はpHの増加ともに減少し、水酸化物の生成によりpH9〜11においてほぼ一定となるが、pH11以上で再び溶解度が増加する。したがって、水浄化において亜鉛を除去するときには、pH9〜11の範囲に設定すればよいことが理解できる。
注意事項2
上記の平衡式(3)~(7)は生成型で示してある。解離型で示すと、”=”の左辺と右辺が逆になり、pK値の正負の符号も逆になる。一般的には、解離型平衡式のpK値が示されているので、符号に注意する。下記の「MS-Excel自動計算」では、解離型のpKaiを代入する型式となっている。
The relation between the pH value and the concentration C of each dissociated species is shown in Fig.2 using the relational expressions (8) to (13) .
As shown in Fig.2 , the solubility of zinc (II) decreases with increasing pH and becomes almost constant at pH 9 to 11 due to the formation of hydroxide, but the solubility increases again at pH 11 and above. Therefore, it can be understood that when removing zinc in water purification, the pH should be set within the range of 9 to 11.
Note 2
The above equilibrium equations (3) to (7) are shown as generative-type. In dissociative form , the left and right sides of “=” are reversed, and the positive and negative signs of pK-values are also reversed. In general, the dissociation-type equilibrium pK-value is shown, so be careful of the sign. In the “MS-Excel automatic calculation” described below, it is a model in which the dissociation type pKai is applied.
log[Zn2+] = 12.45– 2pH (8)
log[ZnOH+] = 3.49 – pH (9)
log[Zn(OH)2(aq)] = -4.45 (10)
log[Zn(OH)3–] = -15.95 + pH (11)
log[Zn(OH)42-] = -28.75 + 2pH (12)
log ZnTotal = log([Zn2+] + [ZnOH+] + [Zn(OH)2(aq)] + [Zn(OH)3–] + [Zn(OH)42-]) (13)
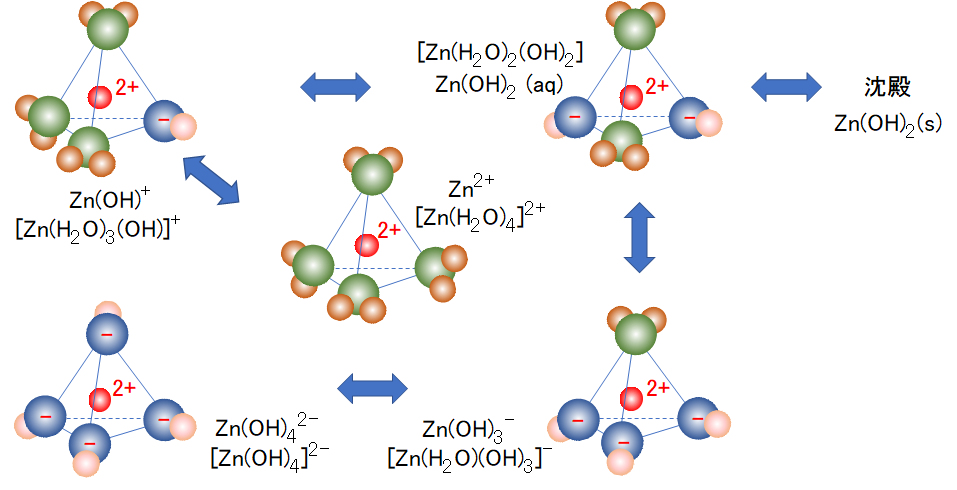
図1 水和亜鉛(Ⅱ)の錯イオン
原子と球の色: 赤-Zn、緑・青-O、茶・桃-H
なお、沈殿生成の過程は複雑である。興味ある方は、別ページを参照のこと。
Fig.1 Complex ion of hydrated zinc (II)
Atom and sphere color: Red-Zn, green/blue-O, brown/peach-H
The process of precipitation formation is complicated. If you are interested, please refer to another page.
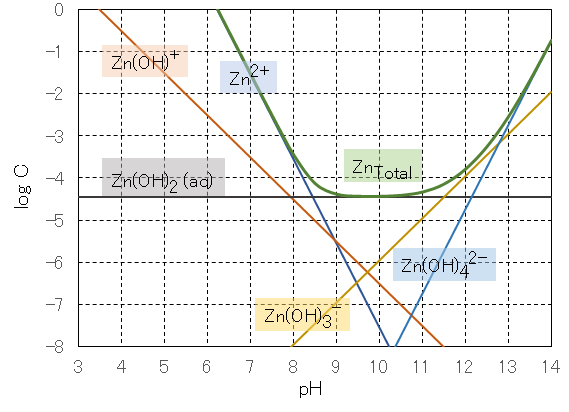
図2 亜鉛(Ⅱ)の溶解度とpHとの関係
Fig. 2 Relationship between solubility of zinc (II) and pH
(2)アルミニウム(Ⅲ)
アルミニウム(Ⅲ)の水和イオンの各解離種の構造を図3に示し、各解離種の簡略式を併せて示す。この簡略を用いて、各解離種の平衡式およびそれぞれの平衡定数は式(14)~(18)で示される。なお、学習のため、アルミニウム(Ⅲ)については上記(1a)の表記法を用いている。
各平衡式(14)~(18)から、各解離種の濃度は式(19)~(23)で示される(なお、詳細な導入式および計算表は下記に示す)。
式(19)〜(24)の関係式を用いて、pH値と各解離種の濃度Cの関係を図4に示す。この図に見られるように、アルミニウム(Ⅲ)の溶解度はpHの増加ともに減少し、水酸化物の生成によりpH7付近に極小値があり、このpH以上で再び溶解度が増加する。したがって、水浄化においてアルミニウム(Ⅲ)を除去するときには、汚水を中性に設定すればよいことが理解できる。
(2) Aluminum (Ⅲ)
The structure of each dissociated species of the hydrated ion of aluminum (III) is shown in Fig.3, and the simplified formula of each dissociated species is also shown. Using this simplification, the equilibrium equations for each dissociated species and their equilibrium constants are given by equations (14)-(18). For learning, the notation of (1a) above is used for aluminum (III).
From each equilibrium formula (14) to (18), the concentration of each dissociated species is represented by formulas (19) to (23) (the detailed introduction formula and calculation table are shown below).
The relation between the pH value and the concentration C of each dissociated species is shown in Fig.4 using the relational expressions (19) to (24). As shown in this figure, the solubility of aluminum (III) decreases with increasing pH, and there is a minimum value around pH 7 due to the formation of hydroxide, and the solubility increases again above this pH. Therefore, it can be understood that when removing aluminum (III) in water purification, the wastewater should be set to neutral.
Al3+ + H2O = AlOH2+ + H+: pK = 4.97 (14)
Al3+ + 2H2O = Al(OH)2+ + 2H+: pK = 9.3 (15)
Al3+ + 3H2O = Al(OH)3(aq) + 3H+: pK = 15.0 (16)
Al3+ + 4H2O = Al(OH)4– + 4H+: pK = 23.0 (17)
Al3+ + 3H2O = Al(OH)3(s) + 3H+: pK = 10.8 (18)
log[Al3+] = 10.8 -3pH (19)
log[AlOH2+] = 5.83 – 2pH (20)
log[Al(OH)2+] = 1.5 – pH (21)
log[Al(OH)3(aq)] = -4.2 (22)
log[Al(OH)4–] = -12.2 + pH (23)
log AlTotal = log([Al3+] + [AlOH2+] + [Al(OH)2+] + [Al(OH)3(aq)] + [Al(OH)4–]) (24)
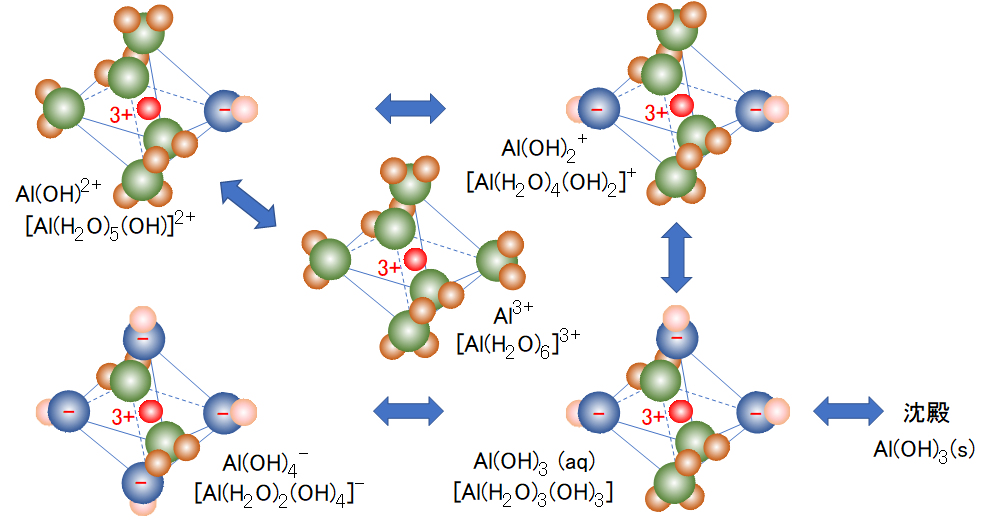
図3 水和アルミニウム(Ⅲ)の錯イオン
原子と球の色: 赤-Al、緑・青-O、茶・桃-H
なお、沈殿生成の過程は複雑である。興味ある方は、別ページを参照のこと。
Fig.3 Complex ion of hydrated aluminum (Ⅲ)
Atom and sphere color: red-Al, green/blue-O, brown/peach-H
The process of precipitation formation is complicated. If you are interested, please refer to another page.
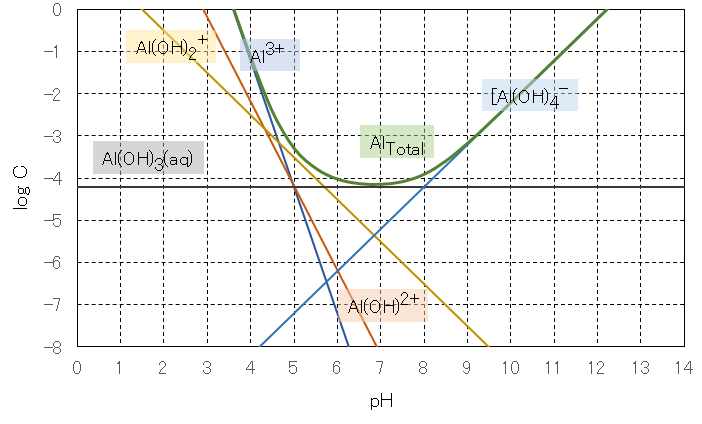
図4 アルミニウム(Ⅲ)の溶解度とpHとの関係
Fig.4 Relationship between solubility of aluminum (Ⅲ) and pH
3.留意事項
水溶液反応に影響を与える共存物質がある場合には、金属イオンの挙動は様々に異なる。また、実際にpHと金属イオンの溶解度の関係を測定すると、平衡定数から理論的に求めたものとは一致しないことが多々ある。
この理由として、水溶液の温度、イオン強度(電解質濃度)、pH測定範囲、溶存種の数、溶存濃度(飽和溶液に用いる水酸化物として、結晶かアモルファスか)の測定条件や分析方法の違いなど、様々な要因がある。これまでに求められている平衡定数の値には、研究者によって差異が見受けられる。各要因について個々に言及することは、このページの目的ではないのでここでは割愛する。
実際の天然水中の金属イオンの挙動や用・排水から有害な金属イオン(人の健康や生態系に有害なものおよび用水において阻害作用を示すもの)を除去する方法として、中和やpH調整による難溶性金属水酸化物の沈殿法は広く活用されている。
実験計画や処理設計において、平衡定数に基づく理論値は極めて有益な指針を与えるものである。しかし、具体的に本法を採用するにあたっては、実際に実験を行って、その最適条件を決定することに留意する。
3. Notes
The behavior of metal ions varies in the presence of coexisting substances that affect the reaction in aqueous solution. In addition, when the relationship between pH and the solubility of metal ions is actually measured, it often does not match the theoretically obtained equilibrium constant.
Reasons for this include differences in the temperature of the aqueous solution, ionic strength (electrolyte concentration), pH measurement range, number of dissolved species, dissolved concentration (whether the hydroxide used in the saturated solution is crystalline or amorphous), and analysis methods, etc. , There are various factors. There are differences in the values of the equilibrium constants that have been obtained so far, depending on the researchers. It is not the purpose of this page to mention each factor individually, so I will omit them here.
As a method of removing harmful metal ions (harmful to human health and ecosystem and showing inhibitory effect on water) from the actual behavior of metal ions in natural water and water/wastewater, neutralization and pH adjustment are used. The method of precipitating a poorly soluble metal hydroxide is widely used.
The theoretical value based on the equilibrium constant gives a very useful guide in experimental design and treatment design. However, it should be noted that when adopting this method specifically, actual experiments are performed to determine the optimum conditions.
4.計算
図2についての計算は、MS-Excelの縦欄にpHの値、横欄に式(8)~(12)より各解離種の対数値とその実数値を求める。次に、各実数値の総計を求め、その対数値より式(13)の値を求める。これをグラフ化すれば、図2が得られる。図4についても、同様である。
4. Calculation
In the calculation for Fig.2 , the pH value is shown in the vertical column of MS-Excel, and the logarithmic value of each dissociated species and its real value are obtained from Eqs. (8) to (12) in the horizontal column. Next, the total of each real value is calculated, and the value of equation (13) is calculated from the logarithmic value. If this is graphed, Fig.2 is obtained. The same applies to Fig.4
興味ある学生さんは、実際に計算してみてください。次の自動計算例では、上記<注意事項2>で示した解離型平衡式の各pKaiを入力してください。入力欄は「黄色」塗りの枠で示す、① 金属元素の記号、② 価数 m、③ 配位数 n、④ 溶解度積 pKsp、⑤ 解離定数 Kai (i=1~n) です。グラフも自動的に表示されます。
なお、水酸化物沈殿はコロイド状を示すことが多く、その溶解度積を実験的に求めることが難しく、〇~△のようにある範囲で示されていることが多い。④の欄には、下限と上限の値を入力してください。1つの値の場合には、同じ値を入力してください。文献値を引用するとき、平衡式中の分子式について、上記<注意事項1>に留意してください。
Zn2+、Cd2+、Pb2+、Al3+の4例を掲載
If you are an interested student, please try the actual calculation. In the following automatic calculation example, enter each pKai value of the dissociation type shown in Note 2 above. The input field is indicated by a frame marked with “yellow”: ① metal element symbol, ② valence m, ③ coordination number n, ④ solubility product pKsp, ⑤ dissociation constant Kai(i = 1 to n). The graph is also displayed automatically.
It should be noted that hydroxide precipitates often show a colloidal form, and it is difficult to experimentally determine the solubility product thereof, and they are often shown in a certain range such as ○ to Δ. Enter the lower and upper limit values in the ④ column. If there is only one value, enter the same value. When quoting literature values, please note “Note 1” above regarding the molecular formula in the equilibrium formula.
Four examples are show for Zn2+, Cd2+, Pb2+, Al3+
Appendix
Since the visitors to this page inquired about the procedure for obtaining the concentration Eqs. (8) to (12) from the equilibrium Eqs. (3) to (7), it will be described in detail below.
予備知識
以下の計算において、[X]は溶質Xのモル濃度を示し、全ての溶質Xの活量係数は’1’とし、その状態は25℃、1atmとする。pXでは溶質Xの電荷(表示)は省略する。
pX = -log[X] (α)
Prior knowledge
In the following calculation, [X] represents the molar concentration of solute X, the activity coefficient of all solutes X is “1”, and the state is 25° C. and 1 atm. In p X, the charge (display) of solute X is omitted.
pX = -log[X] (α)
反応式:aA + bB = cC + dD
→ 平衡定数:K = [C]c[D]d/[A]a[B]b (β)
平衡定数(β)と各溶質 X の関係を逆対数 pXで示すと、算術和として次式で示される。
pK = cpC + dpD – apA – bpB
よって、反応式(β)は、平衡定数と逆対数を用いて、次式(γ)のように表示できる。
apA + bpB = cpC + dpD – pK (γ)
*なお、一般的に平衡反応において、水の濃度[H2O]は一定としK値に含まれており、固体についてはその活量を’1’として扱っている。
Reaction formula: aA + bB = cC + dD
→ Equilibrium constant: K = [C]c[D]d/[A]a[B]b (β)
When the relationship between the equilibrium constant (β) and each solute X is shown by the antilogarithm pX, it is shown by the following formula as the arithmetic sum.
pK = cpC + dpD – apA – bpB
Therefore, the reaction equation (β) can be expressed as the following equation (γ) by using the equilibrium constant and the antilogarithm:
apA + bpB = cpC + dpD – pK (γ)
* Generally, in equilibrium reactions, the concentration of water [H2O] is constant and is included in the K value. For solids, the activity is treated as ‘1’.
H2O = H+ + OH– → Kw = [H+][OH–]
pKw = pH + pOH (δ)
(pKw = 14.00 at 25℃ & 1atm)
Mm+ + mOH– = M(OH)m(s) → Ksp = [Mm+][OH–]m
pKsp = pM + mpOH
pM = pKsp – mpOH
pM = pKsp + m(pH – 14.00) (ε)
Mm+ + mOH– = M(OH)m(s) → Ksp = [Mm+][OH–]m
pKsp = pM + mpOH
pM = pKsp – mpOH
pM = pKsp + m(pH – 14.00) (ε)
Zn(Ⅱ)の計算
式(8)の導出
式(ε)と式(7)の関係から式(8′)を得て、これを式(α)の関係から式(8)が得られる。
pZn = 15.55 + 2(pH – 14.00)
= -12.45 + 2pH (8′)
log[Zn2+] = 12.45 – 2pH (8)
上記の方法は、pKを溶解度積pKspとして扱ったが、これを平衡定数(β)として扱うと、pK = -15.55(符号に注意)となり、式(γ)を用いて計算しても、次式のように同様な結果として式(8′)が得られる。
pZn + 2pOH = 15.55
pZn = 15.55 – 2pOH = 15.55 – 2(14 – pH)
= -12.45 + 2pH (8′)
式(9)の導出
次に、式(γ)と式(3)の関係から、
pZn + pOH = pZnOH + 5.04
pZnOH = pZn + pOH – 5.04
= pZn + 14.00 – pH – 5.04 (9″)
式(9″)に式(8′)を代入すると、
pZnOH = -12.45 + 2pH + 14.00 – pH – 5.04
= -3.49 + pH (9′)
log[ZnOH+] = 3.49 – pH (9)
式(10)の導出
上記と同様に、式(γ)と式(4)の関係から、
pZnOH + pOH = pZn(OH)2(aq) + 6.06
pZn(OH)2(aq) = pZnOH + pOH – 6.06
= pZnOH + 14.00 – pH – 6.06 (10″)
式(10″)に式(9’)を代入すると、
pZn(OH)2(aq) = -3.49 + pH + 14.00 – pH – 6.06
= 4.45 (10′)
Log[Zn(OH)2(aq)] = -4.45 (10)
式(11)の導出
式(γ)と式(5)の関係から、
pZn(OH)2(aq) + pOH = pZn(OH)3 + 2.50
pZn(OH)3 = pZn(OH)2(aq) + pOH – 2.50
= pZn(OH)2(aq) + 14.00 – pH – 2.50 (11″)
式(11″)に式(10’)を代入すると、
pZn(OH)2(aq) = 4.45 + 14.00 – pH – 2.50
= 15.95 – pH (11′)
Log[Zn(OH)2(aq)] = -15.95 + pH (11)
式(12)の導出
式(γ)と式(6)の関係から、
pZn(OH)3 + pOH = pZn(OH)4 + 1.20
pZn(OH)4 = pZn(OH)3 + pOH – 1.20
= pZn(OH)3 + 14.00 – pH – 1.20 (12″)
式(12″)に式(11’)を代入すると、
pZn(OH)4 = 15.95 –pH + 14.00 – pH – 1.20
= 28.75 – 2pH
Log[Zn(OH)4] = -28.75 + 2pH (11)
Calculation of Zn(II)
Derivation of Equation (8)
Eq.(8′) is obtained from the relationship between Eqs. (ε) and (7), and this is obtained from Eq.(8).
pZn = 15.55 + 2(pH – 14.00)
= -12.45 + 2pH (8′)
log[Zn2+] = 12.45 – 2pH (8)
In the above method, pK was treated as the solubility product pKsp, but if this is treated as the equilibrium constant (β), then pK = -15.55 (note the sign), and even using Eq.(γ) , Eq.(8′) is obtained as a similar result as the following expression.
pZn + 2pOH = 15.55
pZn = 15.55 – 2pOH = 15.55 – 2(14 – pH)
= -12.45 + 2pH (8′)
Derivation of equation (9)
Next is given from the relationship of Eqs. (γ) and (3),
pZn + pOH = pZnOH + 5.04
pZnOH = pZn + pOH – 5.04
= pZn + 14.00 – pH – 5.04 (9″)
Substituting Eq.(8′) into Eq.(9″) yields,
pZnOH = -12.45 + 2pH + 14.00 – pH – 5.04
= -3.49 + pH (9′)
log[ZnOH+] = 3.49 – pH (9)
Derivation of formula (10)
As the same manner as described above, Eqs. (γ) and (4) give,
pZnOH + pOH = pZn(OH)2(aq) + 6.06
pZn(OH)2(aq) = pZnOH + pOH – 6.06
= pZnOH + 14.00 – pH – 6.06 (10″)
Substituting equation (10 ‘) in the equation (9’),
pZn(OH)2(aq) = -3.49 + pH + 14.00 – pH – 6.06
= 4.45 (10′)
Log[Zn(OH)2(aq)] = -4.45 (10)
Derivation of formula (11)
From the relationship between Eqs. (γ) and (5),
pZn(OH)2(aq) + pOH = pZn(OH)3 + 2.50
pZn(OH)3 = pZn(OH)2(aq) + pOH – 2.50
= pZn(OH)2(aq) + 14.00 – pH – 2.50 (11″)
When substituting Eq.(10′) in Eq.(11′),
pZn(OH)2(aq) = 4.45 + 14.00 – pH – 2.50
= 15.95 – pH (11′)
Log[Zn(OH)2(aq)] = -15.95 + pH (11)
Derivation of formula (12)
From the relationship between Eqs. (γ) and (6),
pZn(OH)3 + pOH = pZn(OH)4 + 1.20
pZn(OH)4 = pZn(OH)3 + pOH – 1.20
= pZn(OH)3 + 14.00 – pH – 1.20 (12″)
Substituting Eq.(11′) in Eq.(12′)
pZn(OH)4 = 15.95 –pH + 14.00 – pH – 1.20
= 28.75 – 2pH
Log[Zn(OH)4] = -28.75 + 2pH (11)
Al(Ⅲ)の計算
式(19)の導出
式(γ)と式(18)の関係から式(19’)を得て(上記*に留意)、これを式(α)の関係から式(19)が得られる。
pAl = 3pH – 10.8 (19′)
log[Al3+] = 10.8 – 3pH (19)
式(20)の導出
次に、式(γ)と式(14)の関係から、
pAl = pAlOH + pH – 4.97
pAlOH = pAl – pH + 4.97 (20″)
式(20″)に式(19′)を代入すると、
pAlOH = 3pH – 10.8 – pH + 4.97
= -5.83 + 2pH (9′)
log[AlOH2+] = 5.83 – 2pH (9)
式(21)の導出
式(γ)と式(15)の関係から、
pAl = pAl(OH)2 + 2pH – 9.3
pAl(OH)2 = pAl – 2pH + 9.3 (20″)
式(20″)に式(19′)を代入すると、
pAl(OH)2 = 3pH – 10.8 – 2pH + 9.3
= -1.5 + pH (21′)
log[Al(OH)2+] = 1.5 – pH (21)
式(22)の導出
次に、式(γ)と式(16)の関係から、
pAl = pAl(OH)3(aq) + 3pH – 15.0
pAl(OH)3(aq) = pAl – 3pH + 15.0 (22″)
式(22″)に式(19′)を代入すると、
pAl(OH)3(aq) = 3pH – 10.8 – 3pH + 15.0
= 4.2 (22′)
log[Al(OH)3(aq)] = -4.2 (22)
式(23)の導出
次に、式(γ)と式(17)の関係から、
pAl = pAl(OH)4 + 4pH – 23.0
pAl(OH)4 = pAl – 4pH + 23.0 (23″)
式(23″)に式(19′)を代入すると、
pAl(OH)4 = 3pH – 10.8 – 4pH + 23.0
= 12.2 – pH (23′)
log[Al(OH)4–] = -12.2 + pH (23)
Calculation of Al(Ⅲ)
Derivation of Equation (19)
Eq.(19′) is obtained from the relationship between Eqs. (γ) and (18) (note the above* ), and Eq.(19) is obtained from the relationship between Eq.(α).
pAl = 3pH – 10.8 (19′)
log[Al3+] = 10.8 – 3pH (19)
Derivation of equation (20)
Next, from the relationship between Eqs. (γ) and (14),
pAl = pAlOH + pH – 4.97
pAlOH = pAl – pH + 4.97 (20″)
Substituting Eq.(19′) into Eq.(20″) yields
pAlOH = 3pH – 10.8 – pH + 4.97
= -5.83 + 2pH (9′)
log[AlOH2+] = 5.83 – 2pH (9)
Derivation of Equation (21)
From the relationship between Eqs. (γ) and (15),
pAl = pAl(OH)2 + 2pH – 9.3
pAl(OH)2 = pAl – 2pH + 9.3 (20″)
Substituting Eq.(19′) into Eq.(20″),
pAl(OH)2 = 3pH – 10.8 – 2pH + 9.3
= -1.5 + pH (21′)
log[Al(OH)2+] = 1.5 – pH (21)
Derivation of Equation (22)
Next, from the relationship between Eqs. (γ) and (16),
pAl = pAl(OH)3(aq) + 3pH – 15.0
pAl(OH)3(aq) = pAl – 3pH + 15.0 (22″)
Substituting Eq.(19′) into Eq.(22″) yields
pAl(OH)3(aq) = 3pH – 10.8 – 3pH + 15.0
= 4.2 (22′)
log[Al(OH)3(aq)] = -4.2 (22)
Derivation of Equation (23)
Finally, Eqs. (γ) and (17) give,
pAl = pAl(OH)4 + 4pH – 23.0
pAl(OH)4 = pAl – 4pH + 23.0 (23″)
Equation (23″) becomes Equation (19′) Is substituted,
pAl(OH)4 = 3pH – 10.8 – 4pH + 23.0
= 12.2 – pH (23′)
log[Al(OH)4–] = -12.2 + pH (23)
掲載日:2017/07/17
更新日:2017/10/11(多数の記号ミスを修正した。本文・数値に変更はない。)
更新日:2018/01/19(図2・図4の詳しい計算手順を追加した。結果に変更はない。一部、記号ミスを修正した。)
更新日:2018/11/25(本ページへの訪問者数が多いので、「金属イオンの溶解度とpHとの関係」を自動計算し、グラフを表示する「Excelファイル」を追加し、これに関連する文章を本文中に追加した。)
更新日:2020年06月15日:英語版の追加
Publication: 2017/07/17
Update: 2017/10/11 (A large number of symbols mistakes modified. The texts and numeric values corrected.)
Update: 2018/01/19 (The calculation procedure was added for Fig.2 and 4. There was no change in the result. Some sign errors were corrected.)
Updated: 2018/11/25 (Since there are many visitors to this page, “Numerical relationship between solubility of metal ion and pH” was automatically calculated by “Excel file” that displays a graph and the explanation related was added in the text.)
Update: June 16, 2020 (English version added)
