村上定瞭(水浄化フォーラム)
Ⅰ.素反応の典型例と濃度変化のパターン
1.単分子反応
2.2分子反応
擬1次反応を含む
3.併発反応
4.逐次反応
5.可逆反応
6.酵素反応
7.触媒反応
8.自触媒反応
9.複合反応と定常状態近似
Ⅱ.素反応の解析と実験
1.微分法
2.積分法
3.分離法と初速度法
4.緩和法
Ⅲ.反応速度定数とその値の決定因子
1.気相反応
2.液体反応
3.界面反応
Ⅳ.電子移動反応
1.電子の受授
2.分子の電子エネルギー
3.活性化状態
4.配向エネルギー
5.電子移動速度の推定
6.電子移動のモデル図
Ⅴ.反応動力学
1.温度と反応エネルギー
素粒子と反応エネルギー
2.分子衝突と化学反応
分子の動力学
3.マーカス理論
溶媒中の電子移動反応
4.電極反応と電流密度
過電圧と電流密度
5.井戸型ポテンシャルと電子移動
量子論と反応速度
6.分子構造と反応速度
分子構造と活性化エネルギー
リンクされていない項目は、執筆準備中である。また、目次の構成と内容が変更されることもあるので、更新日に留意されたい。
Ⅰ.素反応の典型例と濃度変化パターン
本章の目的は、反応物質または生成物の濃度の相対的な時間変化の典型的なパターンを示し、素反応の仕組みとの関係を理解することにある。
<典型反応の速度定数と濃度変化の計算・作図>
各反応における速度定数と物質濃度の経時変化の関係は、素反応の解析に役立つ。本ページの掲載図の全てについて、計算用xlsファイルをサーバーに保存してある。
学生や初心者は、同ファイルをダウンロードして、「具体的に速度定数を入力し、物質濃度の経時変化がどのようなパターンとなるか」について、理解を深めることを勧めます。
1.単分子反応
今、次式に示すように単分子Aが反応して他の分子Pに変化し、
A → P (1-1)
時刻tにおける単位時間dt[s]あたりのA濃度の減少量dA[mol/L/s]が濃度Aの1次に比例するとすると、次式の関係が成り立つ。なお、本来ならAの濃度は[A]で示すべきであるが、簡略化のためAで示す。以下、同様に記載する。
- dA/dt = kA (1-1a)
また、Aのn次に比例するときには、次式で示される。
- dA/dt = kAn (1-1a’)
速度式(1-1a)で示される反応をAについて1次反応という。また、速度式(1-1a’)で示される反応をAについてn次反応という。nは実験的に決定されるもので、整数でない反応もある。この場合には、式(1-1)で示されるような単純な反応ではなくて、複雑な素反応から構成されている。
以下、n = 1の反応について説明する。
上式のk[1/s]は定数で、反応(1-1)の速度定数という。上式を次式のように変数分離する。
dA/A = – kdt (1-1b)
t = 0 → t において、A = Ao → A に変化するとし、式(1-1b)を式(1-c)のように積分すると、式(1-1d)が得られる。ここで、Aoを初濃度という。以下、∫f(x)dx [x = a → b]を関数f(x)をx = a → bの範囲で定積分することと表記する。
∫dA/A [Ao → A] = -∫kdt [0 → t] (1-1c)
ln(A/Ao) = -kt (1-1d)
A/Ao = exp(-kt) (1-1e)
ここで、kの逆数をτ = 1/k [s]として、式(1-1e)のtに代入すると、A/Ao = exp(-1) = 1/e(e = 0.3678・・・)、すなわち、Aが初濃度Aoの1/eになるt = τを反応(1-1)の寿命[s]という。また、A/Ao = 1/2になるときのt = t1/2とすると、式(1-1e)より1/2 = exp(-kt1/2)となり、次式が得られる。
t1/2 = ln 2/k (1-1f)
式(1-1f)からわかることは、式(1-1a)で示す1次反応において、A/Ao = 1/2になる反応時間t1/2を半減期という。
図1-1に示すように、1次反応では、tの経過とともに指数関数的に減少し、τ[s]で初濃度の37%、2τで0.17%、3τで0.03%、4τで0.02%までそれぞれ減少し、3τ(= 3/k)において、ほぼ反応が終了することが分かる。
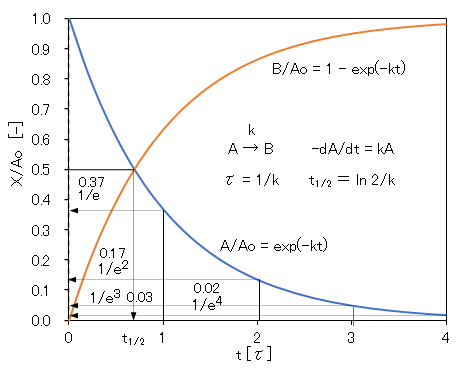
図1-1 単分子(又は原子)の1次反応における反応分子Aおよび生成分子Pの濃度と反応時間tの関係
t:寿命τ[s]を単位とする相対時間、Ao:分子Aの初濃度[mol/L]、X/Ao:Xは分子AまたはPの濃度で、0≦X/Ao≦1である。
目次へ
2.2分子反応
d(P/Ao)/dt ≒ k1S (4-1i)
(1)同分子による2分子反応
-dA/dt = kA2 (2-1a)
式(2-1a)の変数分離式(2-1b)において、t = 0 → t、A = Ao → Aの範囲で積分すると、式(2-1d)が得られる。
dA/A2 = -kdt (2-1b)
∫A-2dt [Ao → A] = -∫dt [t = 0 →t] (2-1c)
1/A – 1/Ao = kt (2-1d)
上式を変形すると式(2-1e)が得られる。
A/[Ao] = 1/(1 + tkAo) (2-1e)
Aについての単分子反応式(1-1e)と2分子反応式(2-1e)を比較すると、単分子反応は速度定数kのみに依存しているのに対して、2分子反応ではkと初濃度Aoの積に依存している。
図2-1に任意の初濃度Aoに対して、8, 4, 2, 1, 1/2, 1/4, 1/8 [αi = 2i ( i = 0, ±1, ±2, ±3)]倍の初濃度Aio(= αi Ao)に設定したときのA/Aioの経時変化を示す。ただし、時間軸は k と任意の初濃度Aoの逆数τ01/2(= 1/kAo、i = 0 のときの反応分子Aの半減期)を単位とする相対時間で示しいている。なお、式(1-1f)に示す1次反応のときの半減期 t1/2と異なることに留意する
この図に見られるように、初濃度Aioが高くなるぼど、A濃度の減少速度が速くなっている。単分子の1次反応では、速度定数kの値は初濃度に関係なく式(1-1f)で決定できるが、2分子反応では、k値の決定には初濃度Aioの絶対値が必要となる。
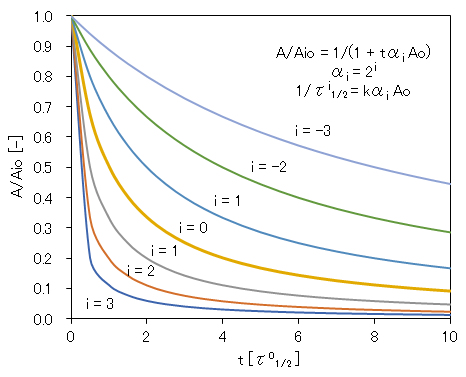
図2-1 同じ分子による2次反応における反応分子濃度の経時変化
Aio:任意濃度Aoに対してαi 倍とした分子Aの初濃度、t:i = 0のときのAio[mol/L]と速度定数k[L/mol/s]の積の逆数τ01/2[初濃度Aio (i = 0)における分子Aの半減期]を単位とする相対時間、
(2) 異分子による2分子反応
A + B → P (2-2)
- d[A]/dt = k[A][B] (2-2a)
AとBの初濃度をそれぞれAoとBo(Ao ≠ Bo)とし、反応時間tにおける反応したAの濃度をxとすると、AとBは1:1で反応するので、tにおけるAとBの濃度は次式で示される。
A = Ao – x (2-2b)
B = Bo – x (2-2c)
Aの減少速度は、次式で示される。
-dA/dt = -d(Ao – x)/dt = dx/dt (2-2d)
式(2-2c)および式(2-2d)を式(2-2b)に代入すると、式(2-2e)の関係から、次式が得られる。
-dx/dt = k(Ao-x)(Bo-x) (2-2e)
-dx/[(Ao-x)(Bo-x)] = kdt (2-2f)
式(2-2e)を変形して変数分離すると、次式となる。
[1/(Ao – x) – 1/(Bo – x)]/(Bo – Ao) = kdt (2-2g)
式(2-2g)をt = 0 → t、x = 0 → xの範囲で積分すると、式(2-2h)が得られる。
∫[1/(Ao – x) – 1/(Bo – x)]/(Bo – Ao)dx [0 → x]
= ∫kdt [0 → t] (2-2h)
[ln(Ao – x) – ln(Bo – x) – (ln Ao – ln Bo)]/(Bo – Ao)
= kt (2-2i)
上式に式(2-2b)と式(2-2c)を代入して、整理すると次式が得られる。
ln[(A/B)(Bo/Ao)] = -k(Bo – Ao)t (2-2j)
単分子1次反応の速度式(1-1e)や同分子の2次反応式(2-1e)では、t に所定の値(相対値)を代入して得られる反応率A/Aoから濃度Aを直接に計算できる。しかし、一般に、異なる2分子の2次反応速度は式(2-2j)で示されているが、時間tをこの式に代入しても、直接に濃度Aまたは濃度Bを計算できない。そこで、同式中のA/Bに式(2-2b)と式(2-2c)を代入して、A/Bの分子/分母をAoで除すると式(2-2k)が得られる。x/Ao(反応率)に所定間隔で値(例えば、0, 0.05, 0.10, 0.15,・・・,0.99)を代入して反応時間tを求め、t を半減期 τ1/2 (= 1/[k(Bo – Ao)])を単位とする相対時間に変換し、反応率A/AoおよびB/Aoとの関係を図2-2に示す。
ln[(1 – x/Ao)/(Bo/Ao – x/Ao)(Bo/Ao)]
= -k(Bo – Ao)t (2-2k)
ただし、0 ≦ x/Ao < 1
図2-2には、Bo/Ao = 2i (i = 1/2, 1, 2, 3)におけるX/Ao(X = AまたはB)の経時変化を示している。AもBも時間とともに減少しているが、濃度差(A – B)は常に一定で、いずれかの曲線を縦軸に沿って平行移動すると、互いに重なることとなる。相対時間τ1/2 (= 1/[k(Bo – Ao)])、Aの半減期)を単位としているが、Bo/Ao値の増加とともに、反応時間が短縮されている。
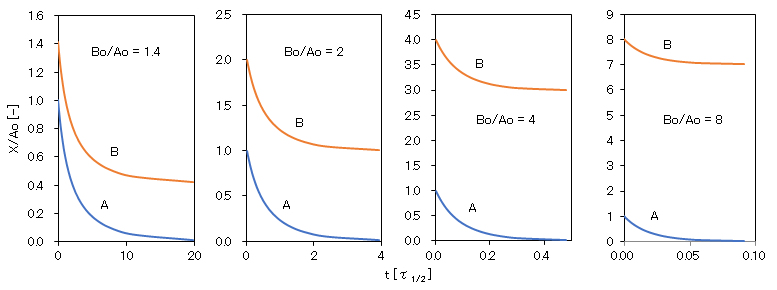
図2-2 異なる2分子による2次反応における反応分子濃度の経時変化
t:分子Aの半減期τ1/2 (=1/[k(Bo – Ao])を単位とする相対時間; Ao、Bo:分子A、Bの初濃度; X/Ao:反応分子AまたはBの濃度のA分子の初濃度Aoに対する比率
(3)疑1次反応
この図には、初濃度の倍率Bo/Aoを1.5、3i (i = 1, 2, 3)としたときの結果を示している。点線で示した経時変化は、Aの単分子1次反応式(1-1e)を用いて、k → kBoとしたときの曲線である。2次反応式(2-2k)と1次反応式(1-1d)の結果は、Bo/Ao(倍率) = 9 以上ではほぼ一致しており、Bo/Ao = 81 ではほぼ完全に一致している。t = τ’と3τ’におけるA/Aoの相対誤差は、倍率9 で4%と18%、倍率27 で1%と6%、倍率81 で0%と2%となっている。
反応速度の測定実験での誤差を勘案すると、Bo/Aoがおよそ30以上であれば、1次反応として扱っても特に問題とならないことが分かる。ただし、k値を求めるときには、AoおよびBoの絶対濃度が必要となる。
以上のことから、Bo ≫ Aoの条件では、B ≒ Bo(ほほ一定)、Bo – Ao ≒ Boとなるので、式(2-2j)と式(1-1d)は同じものとなる。ただし、k → kBoとなる。このように、異なる2分子が反応に関与する2次反応において、他方が過剰に存在するときには、1次反応として扱うことで簡略化できる。これを擬1次反応という。
<留意事項>
分子Aの反応速度を扱う場合、反応に関与する共存分子Bの濃度が高いとき、見かけ上、分子Aの単分子1次反応と判断することになる。特に、液相においては、溶媒分子が反応に関与しているかどうか区別できないので注意が必要である。本章では説明を省略するが、他の実験手法などにより確認することが必要となる。水溶液中の微量分子(又はイオン)の反応では、共存する水分子や共存物質によって大きく影響されることがあるので、浄化プロセスの設計・維持管理において留意すべきことである。
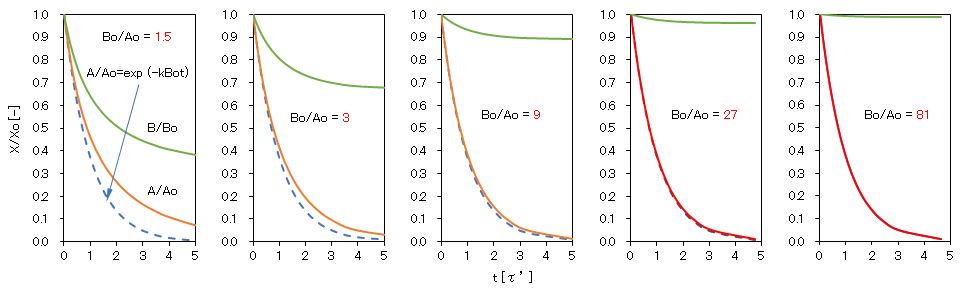
図2-3 擬一次速度反応の反応分子濃度の経時変化
t:分子Aの擬1次反応の寿命τ'[= 1/(kBo)]を単位とする相対時間、X/Xo:反応分子AまたはBの反応率A/AoまたはB/Bo
目次へ
3.併発反応
A → pP + qQ (3-1)
ただし、p + q = 1とする。
A → P (3-1a)
A → Q (3-1b)
dP/dt = kpA (3-1c)
dQ/dt = kqA (3-1d)
反応物質Aの減少速度は、次式で示される。
-dA/dt = kpA + kpA = kA (3-1e)
ただし、k = kp + kq (3-1f)
式(3-1e)は、上式(1-1a)と同じであるので、式(3-1f)の関係からA/Aoは次式で示される
ln A/Ao = -(kp + kq)t (3-1g)
A/Ao = exp[-(kp + kq)t] (3-1h)
式(3-1c)、式(3-1f)およぼ式(3-1h)の関係から、次式が得られる。
dP/dt = kpAo exp(-kt) (3-1i)
上式を変数分離して、t = 0 → t、P= 0 → Pの範囲で積分すると、次式が得られる。
P = (kp/k)Ao[1 – exp(-kt)] (3-1j)
同様に、
Q = (kq/k)Ao[1 – exp(-kt)] (3-1k)
これらの反応は、分子Aに対して1次反応であり、その寿命τは式(3-1m)で示される。
τ = 1/k = 1/(kp + kq) (3-1m)
生成物であるPとQの比率は、式(3-1n)で示され、p/qを分岐比という。分岐比は反応時間によらず常に一定で、それぞれの速度定数の比で示される。
P/Q = kp/kq =p/q (3-1n)
図3-1にkp/kq = 9/1、7/3、5/5、3/7、1/9におけるA/Ao、P/AoおよびQ/Aoの経時変化を寿命τを単位とする相対時間で示す。
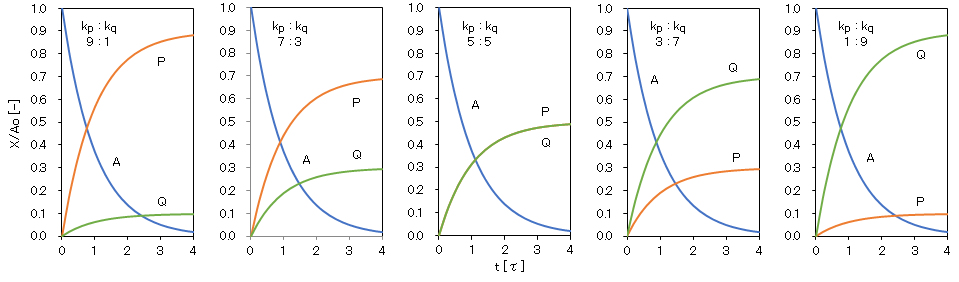
図3-1 併発1次反応での反応分子Aと生成分子PおよびQの経時変化
t:寿命τ[= 1/(kp + kq)]を単位とする相対時間、Ao:分子Aの初濃度、kpとkq:AのPとQへ変化する速度定数
目次へ
4.逐次反応
S → IおよびI → Pへ変化する反応はいずれも1次とし、それぞれの反応速度定数をk1およびk2とする。
k1 k2
S → I → P (4-1)
出発分子S濃度の減少速度は次式で示される。
-dS/dt = k1S (4-1a)
生成分子P濃度の増加速度は次式で示される。
dP/dt = k2I (4-1b)
中間分子Iの濃度変化の速度は、A → Iよる増加速度とI → Pによる減少速度の和であるので、次式で示される。
dI/dt = dS/dt – dP/dt (4-1c)
さらに、全反応時間を通して、S、I、Pの各濃度の総和は、出発分子Sの初濃度Soに等しいので、次式が成立する。
S + I + P = So (4-1d)
式(4-1a~d)の関係から、分子S、I、Pの濃度の経時変化は以下のようになる(詳しい解法は、下記に示す)。
S/So = exp(-k1t) (4-1e)
I/So = [k1/(k2 – k1)][exp(-k1t) – exp(-k2t)]
= 1/(1 – k2/k1][exp(-k2t) – exp(-k1t)] (4-1f)
≒ 0 (k1 ≪ k2のとき) (4-1f-1)
≒ exp(-k2) (k1 ≫ k2のとき) (4-1f-2)
P/So = 1 – exp(-k1t) – k1/(k2 – k1)][exp(-k1t) – exp(-k2t)]
= 1 – exp(-k1t) – [1/(1 – k2/k1)][exp(-k2t) – exp(-k1t)] (4-1g)
≒ 1- exp(-k1t) (k1 ≪ k2のとき) (4-1g-1)
≒ 1- exp(-k2t) (k1 ≫ k2のとき) (4-1g-2)
ただし、上記の近似式は反応開始直後(t = 0およびその近傍)を除く。
式(4-1e~g)を用いて、k1/k2 =1/100, 1/10, 1.01, 10, 100のとき、式(4-1)に示す各分子の濃度変化を図4-1に示す。ただし、反応時間tは、τ1 = 1/k1を単位とする相対時間である。
この図に見られるように、k2/k1の値によって、各分子濃度の経時変化の挙動は大きく異なる。次節で(1)k1 > k2および(2)k1 < k2のケースについて、その挙動を説明する。
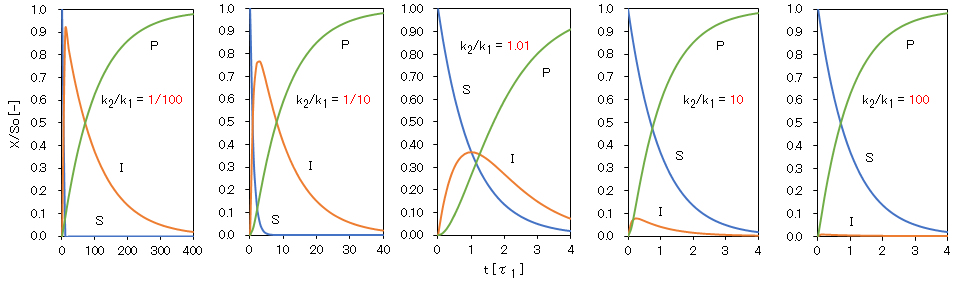
図4-1 逐次1次反応における周発分子S、中間分子Iおよび生成分子Pの濃度経時変化
t:τ(=1/k1)を単位とする相対時間、So:出発分子の初濃度
(1)k1 > k2 の逐次反応
-d(S/So)/dt ≒ d(P/So)/dt ≒ k2S (4-1h)
k1 ≫ k2では、S → I → Pの全反応速度は I → Pの反応速度に依存することとなる。反応 I → Pを逐次反応における律速反応(過程、または段階)という。
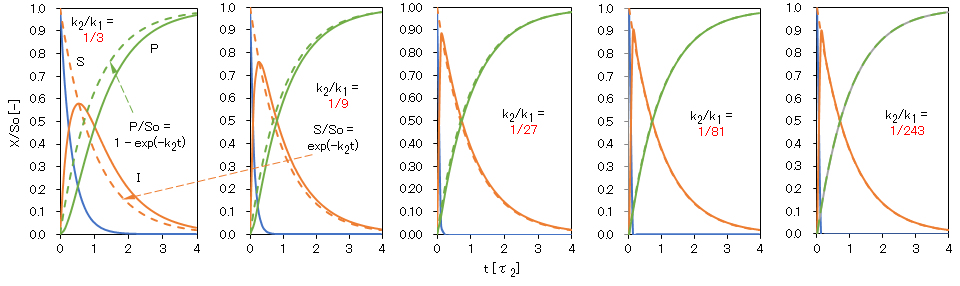
図4-2 I → P(k1 > k2)の反応が律速となる各分子濃度の経時変化
t:τ2 (= 1/k2)を単位とする相対時間、So:出発分子Sの初濃度
(2)k1 < k2 の逐次反応
-d(S/So)/dt ≒ d(P/So)/dt ≒ k1S (4-1i)
k1 ≪ k2では、S → I → Pの全反応速度はS → I の反応速度に依存することとなり、反応S → I が逐次反応における律速反応となる。
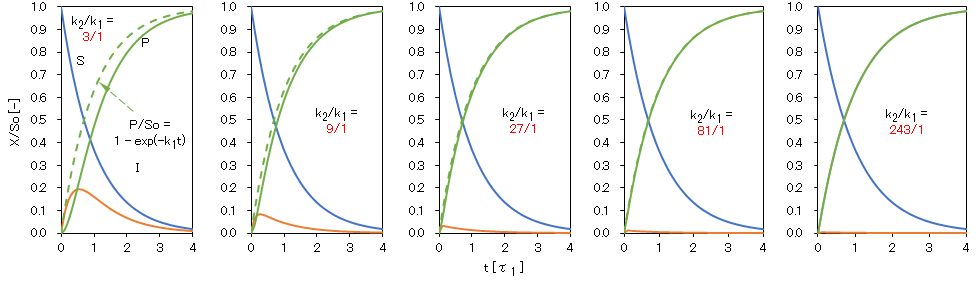
図4-3 S → I(k1 < k2)の反応が律速となる各分子濃度の経時変化
t:τ1 (= 1/k1)を単位とする相対時間、So:出発分子Sの初濃度
<逐次反応の微分方程式の解法>
(後日、掲載)
目次へ
5.可逆反応
k1/k-1
A ⇄ P (5-1)
正・逆の両反応を1次反応とし、正方向へ速度定数をk1、逆方向への速度定数をk-1とすると、それぞれの反応速度v1およびv-1は次式で示される。
v1 = k1A (5-1a)
v-1 = k-1P (5-1b)
ここで、Aを増加または減少させる作用が働くと、逆にPは減少または増加する。いま、Aを減少させる作用が働き、その速度 v とすると、次式(5-1c)が成り立つ。この速度 v は v1 と v-1 の差であるので式(5-1d)となり、これに式(5-1a)と式(5-1b)を代入すると、式(5-1e)が得られる。
v = -dA/dt = dP/dt (5-1c)
= v1 – v-1 (5-1d)
= k1A – k-1P (5-1e)
ある時刻を t = 0とし、そのときのAおよびPの濃度をAoおよびPoとする。反応時間 tにおけるAの反応量 xとすると、次式が得られる。
A = Ao – x (5-1f)
P = Po + x (5-1g)
式(5-1f)より、dA/dt = dx/dt となり、dx/dt = v であるので、
式(5-1f)と式(5-1g)を式(5-1e)に代入して、次式が得られる。
dx/dt = k1(Ao -x) – k-1(Po + x)
= -(k1 + k-1) x + k1Ao – k-1Po (5-1h)
微分方程式(5-1h)を変数分離・積分すると、次式が得られる(詳細は下記に示す)。
x = (k1Ao – k-1Po)/(k1 + k-1)×{1 – exp[-(k1 + k-1)t]} (5-1i)
よって、式(5-1f)および(5-1g)の関係より、次式が得られる。
A = k-1/(k1 + k-1)×(Ao + Po) + (k1Ao – k-1Po)/(k1 + k-1)× exp[-(k1 + k-1)t] (5-1j)
= 1/(k1/k-1 + 1)×(Ao + Po) + (k1/k-1×Ao – Po)/(k1/k-1 + 1)× exp[-(k1/k-1 + 1)t] (5-1j’)
→ k-1/(k1 + k-1)×(Ao + Po) = Aeq (t → ∞) (5-1j∞)
P = k1/(k1 + k-1)×(Ao + Po) – (k1Ao – k-1Po)/(k1 + k-1)× exp[-(k1 + k-1)t] (5-1k)
= 1/(1 + k-1/k1)×(Ao + Po) – (Ao – k-1/k1×Po)/(1 + k-1/k1)× exp[-(1 + k-1/k1)t] (5-1k’)
→ k1/(k1 + k-1)×(Ao + Po) = Peq (t →∞ ) (5-1k∞)
<説明>k1/(k1 + k-1) → 1/(1 + k-1/k1)のように表現するのは、計算プログラムを作成するとき、左では3個の入力データ、右では1個の入力データとなるので、多数のt値に対してAやPの値を求めるとき(特に実験データをシミュレートするとき)、プログラム作成が簡略化されるとともに、使用するPCの負荷を軽減できる。具体的に計算をしない場合には、式が煩雑となるので不要である。
Peq/Aeq = k1/k-1 = K (5-1m)
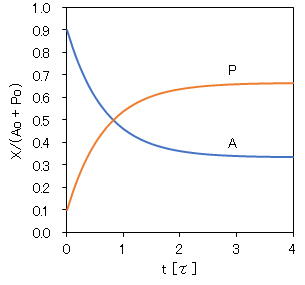
図5-1 可逆反応の反応分子および生成分子の濃度の経時変化
設定値:Ao/(Ao + Po) = 0.9, Po/(Ao + Po) = 0.1, k1/k-1 = 2, τ = 1/(k1 + k-1); t:寿命τを単位とする相対時間
平衡状態に達するまでに要する時間は、正逆の速度定数k1およびk-1に依存する。ここで、式(5-1i)を変形した式(5-1n)で示す反応量比 x/xeq(平衡に達したときの反応量 xeqに対する時間tの反応量 x の比率) の経時変化を寿命τ[=1/(k1 + k-1)]を単位とする相対時間で示すと図5-2のようになる。
反応時間とともに、x/xeq 値は平衡値 xeqへ近づいていく。反応時間τで63% (= 1-1/e)、2τで86%、3τで0.95%、4τで98%にそれぞれx値が平衡値xeqに達する。反応時間が3τ~4τに経過した時点で、ぼほ平衡状態に達していると見なすことができる。
x/xeq = 1 – exp[-(k1 + k-1)t] (5-1n)
ただし、xeq = (k1Ao – k-1Po)/(k1 + k-1)
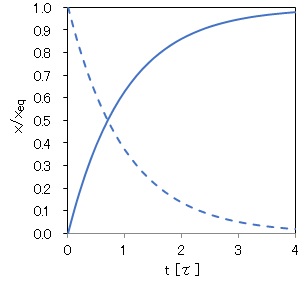
図5-2 可逆反応における反応量 xと寿命τを単位とする経過時間 tの関係
地球環境の自然的または人為的な急激な変化に対して、その変化に対応できる生態システムや社会システムへの構築は個々の種や社会の寿命(対応速度の逆数)に依存し、図5-2に示すような経過をたどることとなろう。
<可逆反応の微分方程式の解法>
(後日、掲載)
目次へ
6.酵素反応
S → P (6-1)
k1/k-1
S + E ⇄ ES (6-1a)
k2
ES → P + E (6-1b)
式(6-1a)で示す反応は、「5.可逆反応」で述べた反応である。生成したESを酵素-基質複合体という(以下、複合体と略称する)。この正反応で生成した複合体ESの一部は逆反応により、基質Sと酵素Eへ戻る。一方で残りの複合体は生成分子Pと酵素Eへと変化し、Eは再び酵素として作用することとなる。
上記の複合体ESが基質Sと生成物Pへ変化する両反応は、「3.併発反応」で述べた反応である。総括反応(6-1)において、Eは再生を繰返し減少することなく、酵素Eと複合体ESの間を行き来するだけである。したがって、次式が成り立つ。
E + ES = Eo (6-1c)
ここで、複合体に対して定常状態近似を適用すると、次式の関係が得られる [この近似については、下記の「9.複合反応と定常状態近似」で説明、式(9-5a)を参照] 。ESSSは定常状態におけるESの濃度である。
dES/dt = k1S・E – k-1ESSS– k2ESSS = 0 (6-1d)
上式に式(6-1c)を代入すると、
k1S(Eo – ESSS) – k-1 ESSS– k2ESSS = 0 (6-1e)
が得られ、ESSSについて整理すると、次式が得られる。
ESSS = k1Eo・S/(k1S + k-1 + k2) (6-1f)
総括反応(6-1)の全速度 vは、Pの生成速度で表すことができるので、反応(6-1b)より速度式(6-1g)が得られ、これに式(6-1f)を代入して速度 vは式(6-1h)で表される。
v = dP/dt = k2ESSS (6-1g)
= k1k2Eo・S/(k1S + k-1 + k2)
= k2Eo・S/[(k-1 + k2)/k1 + S] (6-1h)
上式の分母部分を式(6-1j)に示すMichaelis定数Kmで表示すると、次式が得られる。
v = k2Eo・S/(Km + S) (6-1i)
Km = (k-1 + k2)/k1 (6-1j)
図6-1にSと v の関係を示す。基質濃度Sが高くなり、Km ≪ S になると、酵素反応速度 v → vmax = k2Eoに接近する。また、vmax/2 = Km となるので、このときのS値からKm [mol/L]を決定できる。
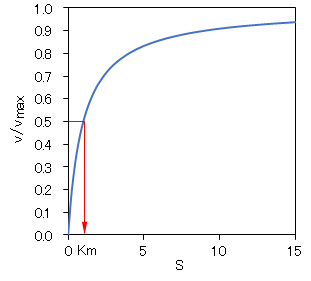
図6-1 酵素反応における基質濃度Sと反応速度 v の関係
vmax = k2Eo、 Eo:酵素複合体を含む酵素の濃度
目次へ
7.触媒反応
触媒反応は、自然現象や生活活用において、多数の事例を挙げることができる。例えば、クロロフルオロカーボンによるオゾン破壊、プラスチック製造、燃焼ガス中の脱硝などである。
ここでは、酸と塩基の触媒反応を取り上げる。水は 2H2O ⇄ H3O+ + OH– のように解離して、ヒドロニウムイオンH3O+(以下、H+と略称)と水酸化物イオンOH–を生成するが、Kw = [H+][OH–] =10-14で電離度は極めて小さい。酸を添加するとH+イオン濃度が増加し、また、塩基を加えると水酸化物イオンOH–が増加する。H+またはOH–あるいは双方が触媒として作用反応し、酸性あるいは塩基性において反応速度が促進される現象は多く見られる。これらを酸-塩基触媒反応という。図7-1(T)に示すエポキシの加水分解も酸-塩基触媒反応を示し、同図に示す反応機構が提案されている。この加水分解の反応速度について、説明する。
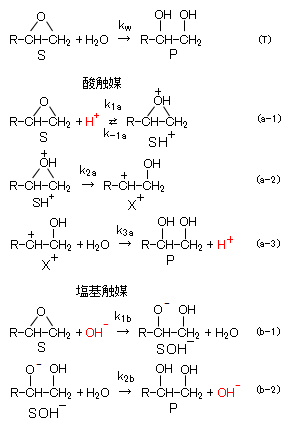
<b>図7-1 エポキシの加水分解の反応機構
反応(a-1)は可逆反応で、正・逆の反応は極めて速く(k1a, k-1a ≫ k2a)、擬似的な平衡状態にある。また、反応(a-2)は反応(a-3)に比べて極めて遅い(k2a ≪ k3a)。このことからH+が関与する全反応速度vHは反応(a-2)に依存し、この反応が律速過程となる。以下、エポキシ分子をS、加水分解生成分子をPで表し、途中過程の分子を同図の記号で示す。H+濃度をHで略記する。
SとSH+は擬似的な平衡状態にあるので、
k1aS・H = k-1aSH+ (7-1a)
SH+ = (k1a/k-1a)S・H (7-1b)
となる。
k2a ≪ k3aであるので、定常状態近似 [9.複合反応と定常状態近似で説明、式(9-2a)を参照] を適用すると、次式となる。
dX+/dt = k2aSH+ – k3aX+ss = 0 (7-1c)
以上より、全反応速度vHは次式で示される。
vH = dP/dt
= k3aX+ss
= k2a/SH+
= k2a(k1a/k-1a)H・S
= kHH・S (7-1d)
ここで、kH = k2a(k1a/k-1a) (7-1d’)
となる。
(b) 塩基触媒反応
OH–の触媒反応による全反応速度vOHは、反応(b-1)が律速(k1b ≪ k2b)であることが提案されている。したがって、vOHは次式で示される [4.逐次反応の「式(4-1g-1)と式(4-1e)の微分式は符号が逆で、速度の絶対値は同じとなる。」を参照]。
vOH = kOHS (7-1e)
ここで、kOH = k1b (7-1e’)
(c) 無触媒反応
エポキシの加水分解反応では、上述の反応(a)および(b)に加え、H+やOH–によらない、中性付近の水反応よばれる反応[図7-1(T)]も存在することが分かっている。この反応による全反応速度vWは次式で示される。
vW = kw[H2O]S
= kw‘S (7-1f)
ここで、kw‘ = kw[H2O] (7-1f’)
溶媒の水分子濃度はほとんど変化しないとする[2.(3)擬1次反応を参照]。
(d) 総括反応
総括反応速度vTは、酸触媒反応速度vH、無触媒反応速度vWおよび塩基触媒反応速度vOHの総和となるので、式(7-1d~f)から次式が得られる。
vT = vH + vW + vOH
= ( kHH + kw‘ + kOHOH)S
= kTS (7-1g)
ここで、kT = kHH + kw’ + kOHOH (7-1g’)
(e) pH-log k の関係
上記式(7-1g’)の両辺の対数を次式で示す。
log kT = log (kHH + kw’ + kOHOH) (7-1h)
さらに、左辺の各項の対数を次に示す。
log kH = log kH – pH (7-1ha)
log kw‘ = log kw‘ (7-1hc)
log kOH = log kOH – pOH (7-1hb)
式(7-1h)および式(7-1ha~hc)について、pH-log k の関係を図7-2に示す。
各pH域では、下記の反応が支配的となり、総括速度定数 kT[/s]は次に示す各速度定数に近似できる。
酸性域:酸触媒反応(a) → kT ≒ kHH [= k2a(k1a/k-1a)] (7-1d’)
中性域:無触媒反応(c) → kT ≒ kw‘ (= kw[H2O]) (7-1e’)
塩基性域:塩基触媒反応(b) → kT ≒ kOH (= k1b) (7-1f’)
さらに、pH = 0, 7, 14におけるlog kT値より、上記(7-1d’~f’)の値が決定できる。
なお、pHはH+の活量で示されるが、ここでは簡略のため、pH = p[H+]として扱った。
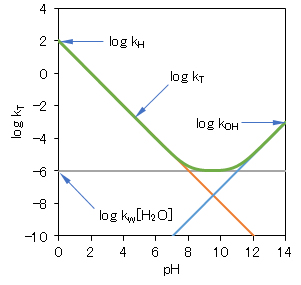
図7-2 エポキシの加水分解反応の総括速度定数 kTの pH依存性
kH = 1.0×102 [/s]、kw‘ = 1.0×10-6 [/s]、kOH = 1.0×10-3 [/s]
緑線:式(7-1h)、橙線:式(7-1ha)、グレイ線:式(7-1hc)、青線:式(7-1hb)
<説明>
酸触媒反応
(a1) 反応(a-1)は極めて速い可逆反応である。この反応はプロトンH+の正・逆の移動反応で、H+は原子量1g/モルの軽原子であること、エポキシ基のO原子と溶媒分子H2Oとの水素結合が形成され、後段の反応が進行すると考えると容易に理解できる。
(a2) エポキシ基は平面構造であるのでpz軌道の重なりによる空のπ軌道(sp3 ⇄ sp2-π:両分子軌道のエネルギー差は小さい)により、不足電子1つを3つの原子が分担することで準安定化している。
(a3) 反応(a-2)では、平面構造からsp3単結合(自由回転)に変わり、-CH+-CH2-OHは鎖状ねじれ構造となる(pz軌道の重なりがなくなる)。このときの分子構造(分子軌道)変化のエネルギー障壁によって反応が遅くなる。
(4a) 反応(a-3)では、電子が不足するC+原子(不足電子を1つの原子で担っている)は不安定であるので、-CH+-基は水分子からOH–を奪い、安定な-CH(OH)-基となる。この反応では、C+が水分子H2OのOと結合(求核反応)し、そのH+が他のH2Oへ移動する。この反応は、分子構造(分子軌道)に大きな変化はないので、速やかに進行する。
塩基触媒反応
(b1) 反応(b-1)は、エポキシ基のO原子がOH–と結合(求電子反応)し、安定なエポキシ平面構造を壊して、上記(a3)で述べた鎖状ねじれ構造(自由回転)へ変化する反応であり、この構造変化のエネギー障壁によって反応が遅くなる。
(b2) 反応(b-2)は、=CH-O–基のO–が水素結合しているH2OからH+を奪って、OH–を解離する反応である。この反応では、分子構造(分子軌道)に大きな変化はないので速やかに反応が進行する。
速度定数
以上の内容を踏まえた上で、具体的な反応速度定数について考察する。
一般的に、k1a = 1010 [L/mol/s] レベルと桁違いに速い反応である。この逆反応速度は物質によって異なるが、有機酸で見られる値 k-1a = 105 [/s] レベルとすると、kH= k2a(k1a/k-1a) [式(7-1d’)] = 102 より、k2a = 10-3 (= k2b = kOH) [/s]となる。このことから、反応(a-2)および反応(b-1)は同レベルの速度となる。エポキシ基の触媒-加水分解反応は、平面構造から鎖状ねじれ構造へのエネルギー障壁(酸と塩基で、同じ速度)、すなわち、分子軌道の変化(sp3 ⇄ sp2-π → sp3)のエネルギー障壁が律速であることを示唆している。
無触媒反応
それでは、式(T)で示す反応定数は上記の酸-塩基触媒反応の律速反応に比べて、10-3倍と極めて遅い。この原因はどこにあるのだろうか。
(1c) 分子H2Oは、少し歪んだ正四面体の中心にO原子、その2頂点にH原子が位置する構造(∠H-O-H = 104°で、Oを頂点とする二等辺三角形で、これを含む面をσvyz面とする)である。
(2c) 酸-塩基触媒で述べたように、エポキシ基のOとH2OのHが水素結合を形成するまでの状況は同じである。しかし、エポキシ基とH2Oの結合反応は、次の条件を満足しないと進行しない。H-OHの結合軸(2等辺の一つ)がエポキシ-三角辺の-O-CH2-辺に平行であってH2OのHおよびOは、エポキシ基の-O-と-CH2-にそれぞれ対応する位置にあり、さらに、H2O分子のσvyz面とエポキシ骨格を含む面が重なる状態(-CH2-基の2つのHとの立体障害を避けるために)で、H-OH軸上にないHはエポキシ基側と反対側の位置にあって、相互の分子軌道がそれぞれ重なる距離にまで接近すること。このような2分子の接近条件は立体図面によって簡単に示されるが、確率を計算するためには、各条件確率の全積が必要であり、文章で表現した。水溶液中では、エポキシ分子全体もH2O分子も自由に並進・振動・回転(気相反応に比べて、水相反応ではある程度の制限があるが、逆に周囲の水分子は構造化)している中で、上記のような条件で接近する確率(p)は極めて低い。このような状態の後、H2O分子のH-OHの結合が切れてエポキシ基の-O-と-CH2-とが、それぞれ結合して平面構造が壊れ、鎖状ねじれ構造への変化が進行し加水分解反応が完了する。
(c3) この無触媒反応の構造(分子軌道)変化のエネルギー壁の高さが、上記の酸-塩基触媒反応の構造変化の壁と同じ高さであると仮定すると、kw‘= p・k2aとなり、上記の条件でエポキシ基と水分子が接近する確率は p = 10-3となる。このp値が妥当であるかどうか、実験的に確認する必要があるが、いずれにしても、上記のような機構が原因で、エポキシ基の無触媒-加水分解の速度が遅くなることは理解できよう。
8.自触媒反応
化学系学生は分析化学実験で、誰も経験する過マンガン酸滴定 [MnO4– + 8H+ + 5e– → Mn2– + 4H2O (硫酸酸性で加熱)] が典型的な例である。この滴定操作の初期においては、反応速度が遅い(滴下したMnO4–の薄いピンク色の消失に時間を要する)。しかし、生成したMn2–が触媒として作用するので、次第に滴定反応が速やか(薄いピンク色の消失が瞬時)に進行するようになる。本章では、自触媒反応における、反応分子濃度の経時パターンの特徴を説明する。
k1
A → P (8-1)
Pが上式の触媒として働く反応は次のように示される。
k2
A + P → P + P (8-2)
反応(8-1)および反応(8-2)の速度式の和は、次式で示される。
-dA/dt = k1A + k2A・P (8-3)
Ao、Poをそれぞれの初濃度とし、Aの反応量をx[mol/L]とすると、反応物Aおよび生成物Pの濃度は次式で示される。
A = Ao – x (8-3a)
P = Po + x (8-3b)
また、反応時間を問わず、AとPの総和は一定であるので、
A + P = Ao +Po (8-3c)
式(8-3a)、式(8-3b)を式(8-3)に代入すると、
dx/dt = k1(Ao-x) + k2(Ao – x)(Po – x) (8-3d)
式(8-3d)の変数分離・積分して、x = f(t)を求め、式(8-3a~c)の関係から、A濃度の経時変化は次式で示される(詳しい、解法は下記に示す)。
A/Ao = (k1 + k2Ao + k2Po)/[(k1 + k2Po)exp(k1 + k2Ao + k2Po)t +k2Ao] (8-4)
ここで、
α = k1 + k2Ao + k2Po (8-5a)
β = k1 + k2Po (8-5b)
γ = k2Ao (8-5c)
をすると、式(8-4)は次式で示される。
A/Ao = α/[βexp(αt) + γ] (8-5)
また、反応速度は式(8-5)を微分して、次式で示される。
d(A/Ao)/dt = k1α2exp(αt)/[k1exp(αt) + β]2 (8-6)
この2つの事項が自触媒反応の特徴である。生成物Pの濃度が増加すると、その触媒作用によって反応速度が加速されるが、反応物Aの濃度に減少にともなって反応速度が減速される。この加速と減速の2つの現象により反応速度が極大値を示す。
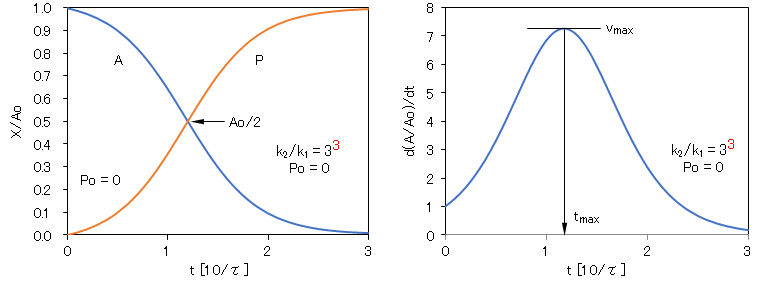
図8-1 自触媒反応における物質濃度(左図)と反応速度(右図)の経時変化
t:τ[=1/(k1 + k2)]を単位とし、その単位の10倍の相対時間で示した。k2/k2 = 3-3 = 1/27、Po(初濃度)= 0 とした。
自触媒反応における速度定数比と初期生成物濃度
自触媒反応において、初期状態から生成物Poを添加したとき(k2/k1 = 102)、その添加濃度に対して、A濃度の経時変化を図8-2(右図)に示した。Po/Ao ≪ 10-2のときには、無添加とほぼ同じである。Po/Ao ≧ 10-2から明確に効果が見られ、添加量の増加に伴い、反応速度が増加している。したがって、反応速度の遅い自触媒反応に対しては、添加濃度PoはPo/Ao ≧ k1/k2とすればよいことがわかる。
以上のことから、k2/k1が数桁の場合には、初濃度Poは、初濃度Aoに対して1/数桁のわずかな量でよいことが理解できる。
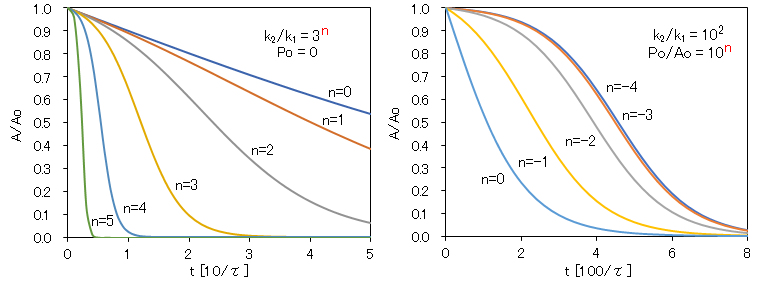
図8-2 自触媒反応における速度定数比 k2/k1(左図)および初期生成物の濃度比 Po/Ao(右図)と反応物質濃度Aの経時変化
t:τ[=1/(k1 + k2)]を単位とし、その単位の10倍(左図)および100倍(右図)の相対時間で示した。
注)左図のn = 0, 1は直線のように見えるが、相対時間軸を延ばすと(例えば、100τ)、右図のようにS字型曲線となる。また、右図のn = 0 の曲線も、相対時間を短縮すると、左図のn = 5に見られるようにシャープなS字曲線となる。
自触媒反応の事例と反応速度式の解法
自触媒反応の事例を示す。また、同事例に反応速度式の解法も示してあるので、興味ある閲覧者は参考にされたい。
目次へ
9.複合反応と定常状態近似
はじめに
(a)定常状態近似の適用の意義
このような場合には、無視できる項を除外したり、ほとんど一定な項を定数として扱い、数式が簡略化され、その近似式を適用することで化学反応を解析することが容易になる。しかも、簡略化された解析結果は、現実の現象や実験結果を十分に満足している。
(b)定常状態近似の明確化
特に、律速過程を伴う複雑な反応においては、その律速となる素反応を明確にしないと、環境汚染対策を講じる場合や、浄化技術の開発・設計・維持管理が適正に実施できない。
反応速度論に関する多くの教科書や講義などにおいて、定常状態近似法は、具体的な反応事項の前に、述べられていることもある。本ページでは、典型的な素反応を例示(既に、近似を適用)した後に、説明する理由もここにある。すなわち、学生や初心者が「そういうことなのか」と理解を深めるためである。素反応における定常状態とは、一見、変化のない、あるいは、観測されないこともあるが、反応が円滑に進行するために極めて重要な過程であることを強調したい。
ここでは、定常状態近似について、既に記載した反応例を挙げて説明する。
溶媒分子が関与する反応は少なくない。水、アルコール、有機酸などがその事例である。「7.触媒反応」で例示した酸-塩基触媒反応で示したように、中性付近の水では極めて遅い反応も、pHを変えることで反応速度が加速される。R-OH + B ⇄ R-O– + HB+などのプロトン移動反応では、正・逆の反応速度が他の素反応と比べ桁違いに速く、下記に述べる前駆平衡反応として取り扱われることが多い。H+は小さな軽い原子であり、原子軌道が異方性のない(対称性)球形である。一方で、酸-塩基触媒の<説明>で記載したように、多原子分子は、質量が大きく嵩張っていて、さらに異方性(非対称性)が加わると、反応物質同士が接近しても、多くの条件が整わないと化学反応が進行しない(反応確率が極めて小さくなる)。
酵素や基質は、カルボキシル基 -C(=O)-OH、ヒドロキシル基 -OH、アミノ基 -N=、などを有し、プロトンH+の受授による水素結合や静電気力(反発力による減速または引力による加速)の有無が極めて重要となる。そのため、至適pHを満たさない条件下では、酵素-基質の鍵穴機能が消失し、酵素-基質複合体の形成が阻害される。酵素反応や触媒反応において、H+(またはOH–)が関与する反応には特に留意が必要である。
上記の溶媒は水素結合によって構造化していること、また、反応物質が溶媒和(化学結合している溶媒分子および静電力によって分極した溶媒分子層の2種類がある)している場合には、反応速度を加速する作用と減速する作用のいずれか、または、双方が働く。
k1 k2
S → X → P (9-1)
式(4-1f)で示すように、k2/k1 の相対比によって、次のように近似できる。
X ≒ 0 (k1 ≪ k2) (9-2)
≒ So・exp(-k2) (k1 ≫ k2) (9-3)
(a) k1 ≪ k2 の反応において、X = 0 ではない
dX/dt = k1S – k2X ≒ 0 (9-2a)
図4-3の k2/k1 ≧ 81 では、中間体 X はほぼ ”0” となっている。あたかも、A の1次反応のように観察されるのである[式(4-1i)参照]。しかし、数式上では“0”と近似しても、中間体Xが存在しないと、反応は進行しないのである。
なお、電極反応において平衡電位Eでは、電流 i = 0 となる。しかし、電極表面では反応が常に進行していて、 i+ – i– = 0 の状態、すなわち、(+)方向と(-)方向の電流が等しくなっているのである。これについては、「Ⅳ.電子移動反応」で説明する。
上記の式(9-2a)は複雑な反応において多用され、その解析を簡略化している。前述の「7.酸-塩基反応」の式(7-1c)は、上式(9-2a)を利用したものである。
ところで、k1 ≫ k2でありながら反応中に X が顕著に認められない反応がある。式(9-4)で示す第1段階が、「5.可逆反応」で述べた可逆(平衡)状態にある反応が存在し、これを前駆平衡反応という。このときのPの生成速度は式(9-4a)で示される。
前駆平衡反応において、k1 ≫ k-1の場合には、S ⇄ X は左(逆)方向に偏っていて、X は極微少濃度で検出されないこともある。k1 ≪ k-1の場合には、右に偏っており、前述した図4-2の k2/k1 ≦ 1/81 に示す挙動となる。
k1/k-1 k2
S ⇄ X → P (9-4)
dP/dt = k1X = (k1/k-1)k2 S (9-4a)
可逆反応で述べたように、平衡状態では正逆反応の速度が等しくなり[式(5-1m)の前文章を参照]、k1A = k-1X → X = (k1/k-1)S となり、上式(9-4a)が得られる。
k1/k-1 k2
S + E ⇄ ES → P + E (9-5)
反応中間体ESの変化速度は次式(9-5a)で示され、これを、式(9-2)に示す定常状態では、”0”と近似するのである。
dES/dt = k1E・S – k-1ES – k2ES ≒ 0 (9-5a)
上式の定常状態にあるESをESSSあるいはES*などの添字を付記して示すことが多い。「6.酵素反応」で示した式(6-1d)は、式(9-5a)と同じ速度式となる。
掲載日:2019年11月07日
更新日:2019年11月23日
