Colloids and Interfacial Phenomena
村上定瞭(水浄化フォーラム), Sadaaki Murakami (Water & Solutions Forum)
はじめに
Ⅰ.コロイドと界面現象
1.コロイドとは
2.疎水・親水コロイド
3.疎水コロイドの分散と凝集
4.親水コロイドの塩析
5.会合コロイドとミセル
6.コロイド溶液の物性
Ⅱ.解説
解説(A) 粒子界面の静電気現象
解説(B) 疎水性2粒子系の相互作用
解説(C) 粒子界面電荷の発生
解説(D) 電解質効果とSchulze-Hardy法則
解説(E) 凝集速度
解説(F) 表面張力と界面活性
解説(G) 界面活性剤の特性
解説(H) 吸着エネルギーと平衡式
解説(J) 高分子吸着と分散・凝集
付録:疎水コロイド相互作用の計算ソフト
(ダウンロード)
参考文献
関連ページ
分散・懸濁粒子の凝集分離
注意:本ページは、複数のサブページから構成されているので、目次を基点に閲覧ください。
Introduction
I. Colloids and interfacial phenomena
1. What is colloid
2. Hydrophobic/hydrophilic colloid
3. Dispersion and aggregation of hydrophobic colloid
4. Hydrocolloid salting out
5. Association colloids and micelles
6. Physical properties of colloidal solution
Ⅱ. Explanation
Explanation (A) Electrostatic phenomenon at particle interface
Explanation (B) Interaction of hydrophobic two-particle system
Explanation (C) Generation of particle interface charge
Explanation (D) Electrolyte effect and Schulze-Hardy law
Explanation (E) Aggregation rate
Explanation (F) Surface tension and surface activity
Explanation (G) Characteristics of surfactant
Explanation (H) Adsorption energy and equilibrium formula
Explanation (J) Polymer adsorption and dispersion/aggregation
Appendix: Calculation software for hydrophobic colloid interaction (download)
References
Related page:
Aggregative separation of dispersed/suspended particles
Note: This page consists of multiple sub pages, so please browse from the table of contents.
はじめに
コロイドおよびその現象は、生命を含む自然界において重要な役割を担い、人々の生活・産業においても様々な形で利用されている。水浄化の分野においても、コロイドの制御は主要な要素技術である。
水浄化において、原水中の濁質のうち、粒子径が10μm程度以上のものは単純な沈澱によって除去することが可能である。しかし、粒子径が1μm以下になると、コロイド粒子が懸濁状となり、ほとんど沈降せず、また急速ろ過では捕捉することもできない(図1)。さらに水中に溶解している有害な金属や非金属の原子・分子イオンを難溶性塩や水酸化物(共同沈殿を含む)として析出・沈降して分離除去するとき、1μm以下の微細な結晶性・不定形の粒子を生成するが、10μm程度以上の沈降性粗大粒子にまで成長できない例は少なくない。
わが国の水道における浄水処理において、一般的に、凝集・沈殿・急速砂ろ過を基本としたシステムが採用されている。この技術が微粒子の分離に優れ、安価・大量処理など多くの利点あるため、日本の近代水道が発祥して100年以上経過した現在でもなお主流技術として用いられている。また、種類の異なる様々な懸濁水(溶解性物質を不溶性物質へ変換する工程も含めて)は、建築・建設工事現場や生産・製造工程において発生し、凝集・沈殿分離は基本的な水浄化技術となっている。
以上の凝集工程の設計や維持管理(目次、関連ページ、参照)を適正に実施するためには、コロイドの性質とその分散・凝集の機構を理解することが大切となる。
Introduction
The colloid and its phenomenon play an important role in the natural world including life, and are also used in various forms in people’s lives and industries. Even in the field of water purification, controlling colloids is a major elemental technology.
In water purification, suspended matter in raw water having a particle size of about 10 μm or more can be removed by simple precipitation. However, when the particle size is less than 1 μm, the colloidal particles become suspended, hardly settled, and cannot be captured by rapid filtration (Fig.1). Furthermore, when separating and removing harmful metal or non-metal atomic or molecular ions dissolved in water as sparingly soluble salts or hydroxides (including co-precipitation), fine crystallinity of 1 μm or less. There are many cases in which irregular particles are generated, but it is not possible to grow to sedimentable coarse particles of 10 μm or more.
Generally, the system based on flocculation/sedimentation and rapid sand filtration is adopted for water purification treatment in Japanese water supply. Since this technology is excellent in separating fine particles and has many advantages such as low cost and large-scale processing, it is still used as the mainstream technology even more than 100 years after the modern Japanese waterworks started. In addition, various types of suspended water (including the process of converting soluble substances to insoluble substances) are generated at construction and construction sites and production/manufacturing processes, and coagulation/sedimentation is a basic water purification. It has become a technology.
In order to properly carry out the design and maintenance of the aggregation process (See Table of Contents: Related Page), it will be important to understand the properties of colloids and the mechanism of their dispersion and aggregation.
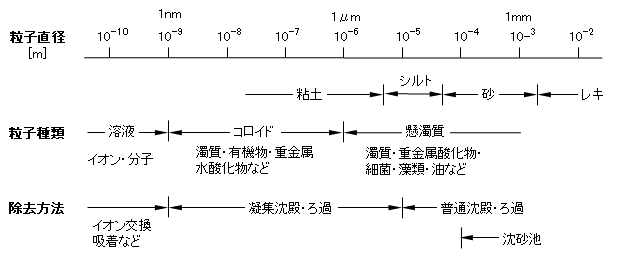
図1 水浄化における汚濁物質のサイズとその分離・除去法
Fig.1 Size of contaminants in water purification and separation/removal method
本ページは、学校・大学の学生や企業での初心者を対象として、「水浄化におけるコロイドの凝集工程についての原理・操作」を理解するための基礎として、「Ⅰ.コロイドと界面現象」、および、「Ⅱ.解説」から構成されている。Ⅰ~Ⅱに記載の内容には、一部、重複したものも含まれている。重複した数式については、サブページを含めて本ページ全体を通して同一の式番号を記載している。
文献・Web-Siteの引用
引用・参考にした文献は本ページボトムに示したが、引用した画像や動画はそれぞれのサイトをリンクしてあるので、それらのサイト内容も含めて理解されたい。
目次へ
This page is intended as a basis for understanding the “Principle and operation of the coagulation process of colloids in water purification” for students at school/university and beginners at companies, composing of “Ⅰ. Colloid and Interface Phenomenon” and “II. Explanation”. The contents described in Ⅰ to II include some duplicates. For duplicate formulas, same formula number is described throughout this page including subpages.
Quotation of literature and web-site
Citations and references are shown at the bottom of this page, but the images and videos cited are linked to each site, so understand the contents of those sites as well.
To table of contents
Ⅰ.コロイドと界面現象
1.コロイドとは
1861年、スコットランドの化学者であるThomas Grahamは、水中でデンプンやタンパク質などの粒子が拡散する速度が遅いことを発見し、これをコロイド(colloid)と名付けた。コロイド粒子(colloidal particle)とは、直径がおよそ1nm~1μm程度で、単一の原子・分子サイズと比べて比較的大きな粒子で、媒体中に分散した状態で存在する。
Ⅰ. Colloid and interfacial phenomena
1. What is colloid
In 1861, Scottish chemist Thomas Graham discovered that particles such as starch and proteins diffuse slowly in water and named it colloid. Colloidal particles are particles with a diameter of approximately 1 nm to 1 μm, which are relatively large compared to a single atomic/molecular size, and exist in a dispersed state in the medium.
1.1 身近なコロイドの事例
コロイドとは、コロイド粒子(固体や液滴)が他媒体(気体・液体・個体)に分散した系全体のことを指す。身近な例でいえば、牛乳や泥水などがコロイドである。牛乳のような分散質が液体コロイドの溶液は一般的にエマルション(emulsion)といい、これに対して、泥水のような分散質が固体コロイドの溶液は一般的にサスペンション(懸濁、suspension)という。
コロイドの分散媒は、液体または固体の場合が多いが、分散媒が気体の場合もあり、そのようなコロイドはエアロゾル(aerosol)という。
ゾル(sol)とは流動性を持ったコロイドのことで、これに対して、加熱や冷却などの何らかの原因で、ゾルが流動性を失ったものをゲル(gel)という。身近なゲルの例としては、寒天・ゼリー・豆腐などがある。
1.1 Examples of familiar colloids
Colloid refers to the entire system in which colloidal particles (solids or liquid droplets) are dispersed in another medium (gas, liquid, solid). In familiar examples, milk and muddy water are colloids. A liquid colloidal dispersoid solution such as milk is generally called emulsion, whereas a solution in which the dispersoid is a solid colloid, such as muddy water, is generally called a suspension.
The dispersion medium of colloid is often liquid or solid, but the dispersion medium may be gas, and such colloid is called aerosol.
A sol is a colloid with fluidity. On the other hand, a sol that loses fluidity due to some reason such as heating or cooling is called a gel. Examples of familiar gels include agar, jelly and tofu.
Table I-1 Classification and examples of familiar colloids.
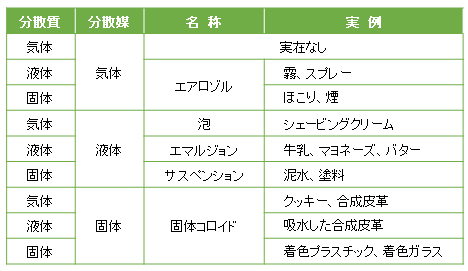
1.2 コロイドの分類
コロイドは、その構造により、① 高分子コロイド(polymer colloid)、② 会合コロイド(association colloid)および ③ 分散コロイド(dispersed colloid)に分類される。
高分子コロイドは、分散媒に分散した分子1個の大きさがコロイドサイズの分散系である。コロイド化学の初期には、高分子コロイドの研究がコロイドの主流であった。コロイド研究の先駆者であったThomas Grahamが最初に示したコロイドは、いずれも天然高分子であった。現在では、高分子化学(polymer chemistry)という別の学問分野ができ上がっているので、高分子をコロイド化学で扱うことは、少なくなった。
会合コロイドは、多くの分子が集まって、コロイドの大きさを持つようになった分散系を示す。洗剤などの界面活性剤分子は、溶液中である濃度以上になると、ミセル(micelle)と呼ばれるコロイドサイズの会合体を形成する。
分散コロイドは、溶媒には本来溶解しない不溶性物質の分散系である。溶解するはずのない物質が媒体中で分散しているのだから、分散コロイドは熱力学的には不安定な系であり、条件によって破壊することができる。表Ⅰ-1で示したコロイドはすべて分散コロイドであり、分散コロイドは最も身近に溢れているコロイドである。
1.2 Classification of colloids
Colloids are classified into 1) polymer colloids, 2) association colloids, and 3) dispersed colloids according to their structure.
Polymer colloid is a dispersion system in which the size of one molecule dispersed in a dispersion medium is a colloid size. In the early days of colloid chemistry, research on polymer colloids was the mainstream of colloids. The first colloid presented by Thomas Graham, a pioneer in colloid research, was a natural polymer. Nowadays, a new discipline called Polymer chemistry has been established, so the handling of polymers by colloid chemistry has decreased.
Associative colloid refers to a dispersed system in which many molecules are gathered and have a colloidal size. Detergents and other surfactant molecules form colloid-sized aggregates called micelles when they reach a certain concentration in solution.
Dispersion colloid is a dispersion system of an insoluble substance that is essentially insoluble in a solvent. Since a substance that should not dissolve is dispersed in the medium, the dispersed colloid is a thermodynamically unstable system and can be destroyed depending on the conditions. The colloids shown in Table I-1 are all dispersive colloids, which are the most common colloids.

1.3 コロイドの形状と観察
(1) 大きさ
コロイド粒子の大きさは直径が1nm~1μmの範囲で、ろ紙を通過するが半透膜を通過しない程度の大きさである。この性質を使用して分子とコロイド粒子を分けることができる。
1.3 Shape and observation of colloids
(1) Size
The colloidal particles have a diameter in the range of 1 nm to 1 μm, and are so small that they pass through the filter paper but not through the semipermeable membrane. This property can be used to separate molecules from colloidal particles.
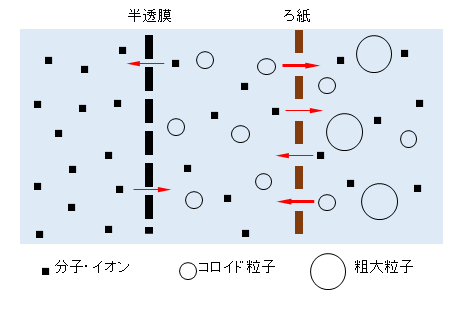
図Ⅰ-1 コロイド粒子の大きさとその分離
Fig.I-1 Colloid particle size and separation.
(2) 形状
コロイド粒子の形状には、球状、棒状、針状、板状、繊維状、膜状のものなど、コロイド系の物質・分散媒やその生成過程を含めて物理・化学的条件により様々な形状で存在している。
(2) Shape
The shape of the colloidal particles may be spherical, rod-shaped, needle-shaped, plate-shaped, fibrous, film-shaped or the like, and may be various shapes depending on the physical and chemical conditions including the colloidal substance/dispersion medium and its generation process. Existing.
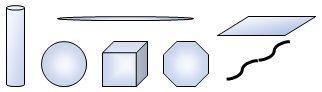
図Ⅰ-2 コロイド粒子の形状モデル Fig.I-2 Colloid particle shape model
(3) 観察
コロイド粒子は、光学顕微鏡では小さすぎて観察することができないが、限外顕微鏡や透過型電子顕微鏡(TEM)などを使えば、コロイド粒子を観察することができる。限外顕微鏡では、特殊な照明装置により微粒子の散乱光(チンダル光)を観察して、微粒子の動きを見ることができる。また、透過型電子顕微鏡では、可視光の代わりに電子線を照射して、対象を観察することができる。コロイド粒子は非常に小さいので、これを観察するには特殊な装置が必要となる。
(3) Observation
Although colloidal particles cannot be observed with an optical microscope because they are too small, colloidal particles can be observed with an ultramicroscope or a transmission electron microscope (TEM). With an ultramicroscope, the movement of the particles can be seen by observing the scattered light (tindal light) of the particles with a special illumination device. Further, in a transmission electron microscope, an object can be observed by irradiating an electron beam instead of visible light. The colloidal particles are so small that special equipment is needed to observe them.

動画Ⅰ-1 限外顕微鏡によるコロイド粒子のブラウン運動の観察(動画は上記画像をクリック)
出典(Source):https://www.youtube.com/watch?v=WprXsEH4HEo
Movie I-1 Observation of Brownian motion of colloidal particles with an ultramicroscope (click on the image above)
2.疎水・親水のコロイド
2.1 コロイド状態の保持
分散コロイドは、不溶性物質の粒子が媒体中に分散している系のことであって、溶解性物質の溶液とは明確に区別される。溶液は結晶がその物質の構成単位である原子や分子のレベルまで解離して溶媒に溶けている状態であるのに対して、コロイドは多数の原子・分子が集まって1つの粒子(例えば、不溶性の金属酸化物では、1nm粒子でおよそ数百個、1μmでおよそ数×1011個の金属と酸素の原子から構成される粒子)となり、それらが媒体に分散している状態である。単一分子サイズが大きい高分子コロイドなどの例外もあるが、コロイドは、一般的には「多数の原子・分子から構成される集合体が分散媒に分散している系」である。したがって、コロイドとして分散状態を保つためには、いくつかの条件が必要となる。
2. Hydrophobic/hydrophilic colloid
2.1 Retaining colloidal state
A dispersed colloid is a system in which particles of an insoluble substance are dispersed in a medium and is clearly distinguished from a solution of a soluble substance. A solution is a state in which crystals are dissociated to the level of atoms and molecules that are the constituent units of the substance and dissolved in a solvent, whereas a colloid is a collection of many atoms and molecules into one particle (for example, insoluble matter). Metal oxide of 1 nm is about several hundred particles, and 1 μm is about several × 1011 particles consisting of metal and oxygen atoms), which are dispersed in the medium. It is in a state of being. Although there are exceptions such as polymer colloids having a large single molecule size, colloids are generally “systems in which aggregates composed of many atoms and molecules are dispersed in a dispersion medium”. Therefore, some conditions are required to maintain the dispersed state as a colloid.
例えば、結晶・粉末状の食塩NaClやショ糖C12H22O11は、水中ではNa+・Cl–イオンやショ糖C12H22O11の単分子にまで解離・溶解しているので、コロイドとはいえない。食塩やショ糖は、水中では結晶・粉末状の状態よりも、解離して水和したイオン・分子での状態の自由エネルギーが低く、熱力学的に安定であるからである。
(ⅱ)コロイド粒子同士が衝突・凝集し、さらに大きな粗粒子にならないこと
分散コロイドは熱力学的には不安定な系で、コロイド粒子は安定になろうと凝集してより大きな粒子になろうとする作用が働く。コロイド粒子が凝集して大きな粒子になると、単に浮上するか沈降するかという状態となり、コロイドではなくなってしまう。
For example, crystalline/powdered NaCl salt and sucrose C12H22O11 cannot be said to be colloids because they dissociate/dissolve into Na+/Cl– ion and a single molecule of sucrose C12H22O11 in water. This is because salt and sucrose have lower free energy in the state of dissociated and hydrated ions/molecules in water than in the crystal/powder state, and are thermodynamically stable.
(ii) Colloidal particles do not collide with each other and aggregate to form larger coarse particles.
Dispersed colloids are thermodynamically unstable systems, and the action of colloidal particles to flocculate and become larger particles works. When colloidal particles agglomerate into large particles, they simply float or settle and become non-colloidal.
第一の方法は、コロイド粒子の表面を帯電させることである。例えば、後述する図Ⅰ-5に示すように、コロイド粒子の表面を「正」に帯電させたとする。このとき、電気的に中性を保とうとして、表面電荷量と同量の負イオンが過剰にコロイド粒子を取り巻いている。粒子の表面電荷と反対符号のイオンを対イオン(counter ion)といい、このような状態を電気二重層(electric double layer)ができているという。なお、多数の対イオンは粒子表面の電荷に引かれて統計的に分布しているものの、個々のイオンは自由に液中を拡散して遠くまで動くことができる。
ところで、ブラウン運動により2つの粒子が接近し、相互の電気二重層が重なるようになると、図Ⅰ-3に示すように、重複した二重層領域の浸透圧 [= Π(h):h は粒子表面間の距離] の増加による反発力 Po(h)が働き、自由エネルギー [= ∫ Π(h)v(h)dh:h = ∞→hで積分; v(h)は重なり領域の体積] が増大することによって熱力学的に不安定となり、粒子同士の合体を妨げるようになる。
基本的には気体の圧縮に必要な力とそれに要する仕事エネルギーの関係と同じようなものと考えると理解しやすい。ただし、重なり領域内でのイオン濃度分布が均一でないので、計算は複雑となる。
The first method is to charge the surface of the colloidal particles. For example, suppose that the surface of colloidal particles is positively charged, as shown in Fig.I-5 described later. At this time, the same amount of negative ions as the surface charge amount surrounds the colloidal particles excessively in order to electrically maintain neutrality. Ions with the opposite sign to the surface charge of the particle are called counter ions, and such a state forms electric double layer. Although a large number of counter ions are statistically distributed by being attracted by the charges on the particle surface, individual ions can freely diffuse in the liquid and move far.
By the way, when two particles come close to each other due to Brownian motion and electric double layers overlap each other, as shown in Fig.I-3, the repulsive force Po(h) due to the increase of the osmotic pressure [= Π(h): h is the distance between particle surfaces] in the overlapping double layer region acts, and the increase of free energy
[= ∫ Π(h)v(h)dh: h = ∞ → h, integration; v(h) is the volume of the overlapping area] makes it thermodynamically unstable and prevents the particles from coalescing.
Basically, it is easy to understand if it is considered to be similar to the relationship between the force required for gas compression and the work energy required for it. However, since the ion concentration distribution in the overlapping area is not uniform, the calculation becomes complicated.
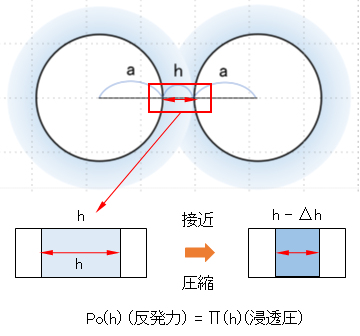
図Ⅰ-3 電気二重層の重なりによる浸透圧の増加と粒子間反発力の発生
Fig.I-3: Increase in osmotic pressure and generation of interparticle repulsive force due to overlapping electric double layers.
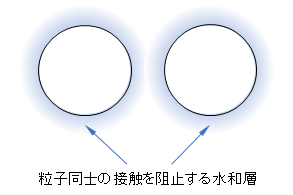
図Ⅰ-4 表面が水素結合による水分子層で覆われている親水性粒子同士の接近
Fig.I-4 Approach of hydrophilic particles whose surface is covered with water molecule layer by hydrogen bond.
2.2 疎水性コロイド
コロイド粒子のうち、主に上記の第一の方法のみで水中で分散している場合、これを疎水コロイド(hydrophobic colloid)という。水に対して不溶であり、本来沈降すべき物質がコロイド粒子のサイズになった上に、何らかの理由(詳しくは、Ⅱ.解説(C)を参照)で表面が帯電してしまったために、粒子間に反発力が働き、合体・集合できなくて微細な状態のコロイド粒子が分散状態になっている。一般的に、疎水コロイドは、その大半が無機物質である。
2.2 Hydrophobic colloid
Among the colloidal particles, when they are dispersed in water mainly by the above-mentioned first method, this is called hydrophobic colloid. Particles that are insoluble in water and should be settled to the size of colloidal particles, and the surface was charged for some reason (see II. Explanation (C) for details) A repulsive force acts between them, and the colloidal particles in a fine state that cannot coalesce and aggregate are in a dispersed state. Generally, most of hydrophobic colloids are inorganic substances.
2.3 親水性コロイド
上記の第二の方法が主たる理由で水中に分散している場合には、これを親水コロイド(hydrophilic colloid)という。コロイド表面に溶媒である水分子層が付着して離れないのは、水に対して親和性が高いからである。親水コロイドには分子コロイドや会合コロイドが多く、その大半が有機物質である。
2.3 Hydrophilic colloid
When the above second method is dispersed in water for the main reason, it is called hydrophilic colloid. The water molecule layer, which is a solvent, adheres to the surface of the colloid and is not separated because it has a high affinity for water. Hydrocolloids are mostly molecular colloids and associated colloids, most of which are organic substances.
Table I-3 Colloid classification and characteristics.

3.疎水コロイドの分散と凝集
3.1 DLVO理論による分散・凝集機構
疎水コロイドは一般的に不安定な系で、粒子表面の電荷密度や溶液の電解質濃度を変化にさせると、分散したり、凝集したりする。この分散・凝集のメカニズムを以下に説明する(各式の誘導はⅡ.解説(B)を参照)。
疎水コロイドの分散・凝集の現象については、粒子の荷電表面による電気二重層による反発力作用および粒子内の構成原子・分子間のvan der Waals引力作用の相反する作用によって理論的に説明することができ、これをDLVO理論という。「DLVO」とは、旧ソ連の化学者であるDerjaguinとLandau、オランダの化学者であるVerweyとOverbeekの4人の研究者の頭文字に由来している。
3. Dispersion and aggregation of hydrophobic colloids
3.1 DLVO theory based dispersion/aggregation mechanism
Hydrophobic colloids are generally unstable systems that disperse or aggregate when the charge density on the particle surface or the electrolyte concentration of the solution is changed. The mechanism of this dispersion/aggregation is explained below (for the derivation of each equation, see Ⅱ. Explanation (B)).
The phenomenon of dispersion/aggregation of hydrophobic colloids can be theoretically explained by the reciprocal action of the repulsive force action by the electric double layer due to the charged surface of the particle and the van der Waals attractive force action between the constituent atoms and molecules within the particle. Yes, this is called DLVO theory. “DLVO” comes from the acronyms of four researchers, former Soviet chemists Derjaguin and Landau, and Dutch chemists Verwey and Overbeek.
(1) 拡散電気二重層
図Ⅰ-5・Aに示すように、電解質溶液中に分散している荷電粒子の界面近傍の溶液側は拡散電気二重層が形成される。この二重層は、次の相反する2つの作用によって説明される。以下、z-z型対称電解質の溶液とする。
(1) 静電気力によって界面電荷(例えば、正の電荷)に対して、反対符号のイオン(対イオン)は界面へ近づくように引力が働き、同符号のイオン(同イオン)は遠ざかるように斥力が働くので、図Ⅰ-5・Cに示すように界面近傍では対イオン個数(n–)と同イオン個数(n+)との濃度差Δn(= n+ – n–; < 0)が生じる。
(2) 一方で、液中では正負の両イオンは熱運動による拡散力がそれらの濃度差Δnを減少させるように働く。
粒子界面から遠ざかるにつれて静電気力が減衰するのに対し、拡散力は一定であるので、遠く離れたところでは、拡散力が支配的となり正負イオンの個数濃度は等しくなる(n+ → n∞、n– → n∞、Δn → 0;n∞は母液中の正負のイオン数)。
(1) Diffused electric double layer
As shown in Fig.I-5・A, a diffusion electric double layer is formed on the solution side near the interface of charged particles dispersed in the electrolyte solution. This bilayer is explained by two opposing actions: Hereinafter, a z-z type symmetrical electrolyte solution will be used.
(1) Due to electrostatic force, an attractive force acts on the interface charge (for example, positive charge) so that ions of opposite sign (counter ion) approach the interface, and ions of the same sign (same ion) repel so that they move away. As shown in Fig.I-5・C, a concentration difference Δn (= n+ – n–; < 0) occurs between the number of counter ions (n–) and the number of same ions (n+) near the interface.
(2) On the other hand, in the liquid, both positive and negative ions work so that the diffusion force due to thermal motion reduces their concentration difference Δn.
While the electrostatic force is attenuated as the distance from the particle interface increases, the diffusive force is constant, so that the diffusive force becomes dominant and the number concentration of positive and negative ions becomes equal (n+ → n∞, n– → n∞, Δn → 0; n∞ is the number of positive and negative ions in the mother liquor).
(2) 電気・拡散二重層を示す基本式
正負の符号が異なるイオン個数が異なると、溶液系のある無限小の体積Δv[m3]が電荷を有するようになり、その密度ρ[C/m3]は次式で示される。
また、拡散層における電荷ρと電位Ψの関係は、次のPoissonの式で示される。
ただし、ε = εrεo、ε:溶媒の誘電率、εs:溶媒の比誘電率、εo:真空の誘電率
式(Ⅰ-1)と式(Ⅰ-2)の関係より、界面電位Ψoとする球形の粒子表面の法線方向をx軸とし、界面からの距離 x[nm]における電位は、次式で近似される。
ここで、κ は式(Ⅰ-9)で示される。
Ψ(x)の分布は、図Ⅰ-5・Bに示すような二重層電位Ψの減衰として表すことができる。
なお、界面電位Ψoは一般に測定困難な量であって、測定可能な「すべり面」における電位(ζ-電位)で近似することが多い。すべり面とは、粒子と液とが相対的に動くときの境界面である。
(2) Basic formula showing electric/diffusion double layer
When the number of ions with different positive and negative signs is different, an infinitesimally small volume Δv[m3] in the solution system has an electric charge, and its density ρ[C/m3] is given by the following equation.
Further, the relationship between the electric charge ρ and the electric potential Ψ in the diffusion layer is expressed by the following Poisson’s equation.
Where ε = εrεo, ε: solvent permittivity, εs: solvent relative permittivity, εo: vacuum permittivity
From the relationship between Equ.(I-1) and Equ.(I-2), the potential at the distance x [nm] from the interface is approximated by the following formula.
Here, κ is expressed by Equ.(I-9).
The distribution of Ψ(x) can be expressed as the decay of the double-layer potential Ψ as shown in Fig.I-5・B.
The interfacial potential Ψo is generally a difficult quantity to measure, and is often approximated by the measurable potential on the “slip surface” (ζ-potential). The slip surface is a boundary surface when particles and liquid move relative to each other.
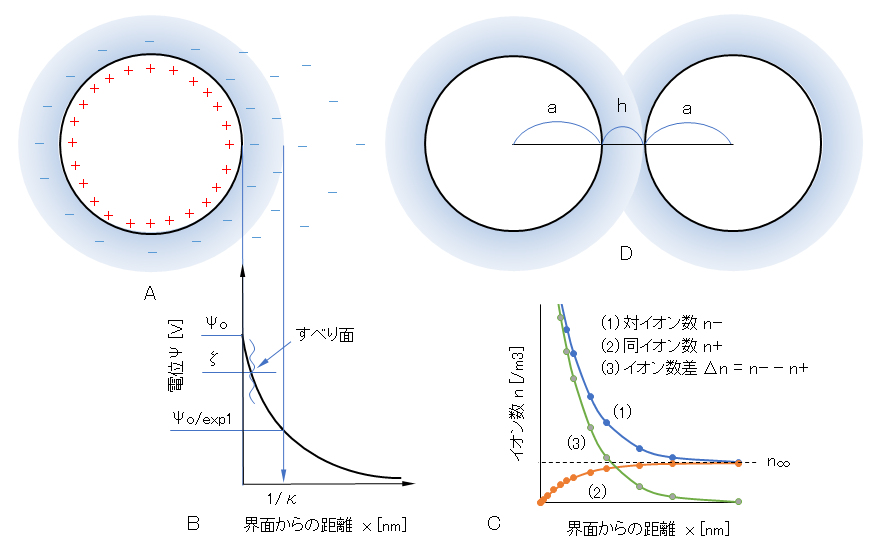
図Ⅰ-5 荷電粒子の電気二重層と2粒子の接近のモデル図
A:電気二重層のモデル、B:固液界面からの距離と電位、C:固液界面からの距離とイオン個数の濃度、D:粒子同士が接近したときの電気二重層の重なり
Fig.I-5 Model diagram of electric double layer of charged particles and approach of two particles.
A: model of electric double layer, B: distance from solid-liquid interface and potential, C: distance from solid-liquid interface and concentration of number of ions, D: overlap of electric double layers when particles approach each other.
吸着性イオン(界面活性剤イオン、高分子イオン、高原子価イオン、錯イオンなど)が存在すると、その濃度に応じた吸着が起こる。吸着イオンの大きさに相当する厚さの吸着層が形成され、その吸着層と溶液との界面に電位(Stern電位Ψδという)が発生する。対イオンはその外側に分布するので、Ψの変化はΨoではなくて、Ψδから出発する(Ⅱ.解説(B)-図B-1(C)を参照)。本章では、吸着性イオンが共存しないコロイド系について議論を行う。
In the presence of adsorptive ions (surfactant ions, polymer ions, high valence ions, complex ions, etc.), adsorption occurs according to their concentration. An adsorption layer having a thickness corresponding to the size of adsorbed ions is formed, and an electric potential (referred to as Stern potential Ψδ) is generated at the interface between the adsorption layer and the solution. Since the counter-ions are distributed on the outside, the change of Ψ starts from Ψδ instead of Ψo (see II. Explanation (B)-Fig.B-1(C)). This chapter discusses colloidal systems in which adsorptive ions do not coexist.
(3) 接近2粒子間に働く力とその系の自由エネルギー
図Ⅰ-5・Dに示すように、球状で半径 aの2つの荷電粒子が接近して、それらの表面の最短距離(2粒子の中心を結ぶ直線とそれらの粒子表面との交点間の距離)をhとする。
粒子同士が接近したとき、斥力PR[N](>0)および引力PA[N](<0)の相反する力が働き(添字、R: repulsion、A:aggregation)、これらの合力は次式で示される。合力P<0であれば、粒子はより接近するように凝集力が働く。合力P>0であれば、粒子は遠ざかるように分散力が働く。
斥力 PRの原因は、疎水コロイドの分散している溶液で、電気二重層を持つ2つのコロイド粒子が接近すると、図Ⅰ-3に示したように電気二重層内の対イオンの重なりにより浸透圧が増大するので、コロイド粒子には反発力が働くからである。
一方で、引力 PAの原因は、コロイド粒子同士がかなり近くまで接近したときには、粒子間にvan der Waals力に起因する粒子間引力が働くからである。
しかし、その粒子系において、「凝集するか、分散するか」は、その系が自由エネルギー的に「安定であるか、不安定であるか」によって決まる。コロイド2粒子系における自由エネルギーVは、斥力および引力に起因するエネルギーVRおよびVAの和として、次式で示される。
2粒子間に働く合力P(h)とその系の自由エネルギーには次の関係がある。
ただし、V(∞) = 0
ここで、Ⅱ.解説(B)で詳述する電気二重層モデルの条件下では、半径 a[m]の2個の荷電粒子が、遠くから粒子界面距離 h[m]に接近したときの合力P(h)および自由エネルギーV(h)は、次式で近似的に示される。
V(h) = 2πaεΨo2 exp(-κh) – aA/(12h) (Ⅰ-8)
κ2 = 2nz2e2/(εkT) (Ⅰ-9)
κ = 3.3×109z√C [/m] (at T = 298K) (Ⅰ-10)
なお、式(Ⅰ-7)~式(Ⅰ-10)において、Ψo:粒子-水界面における電位[V]、ε:水の誘電率(7.08×10-10[N/m2/C2]、25℃)、A:Hamaker定数、z:z-z型対称電解質の価数、n(= n∞ = 1.0×103C):単位体積中の電解質イオン個数[1/m3]、C:電解質濃度[mol/L]である。
(3) Force acting between two approaching particles and free energy of the system
As shown in Fig.I-5・D, two charged particles with a radius of a are close to each other and have the shortest distance h between their surfaces (the distance between the intersection of the straight line connecting the centers of the two particles and their surface).
When particles are close to each other, repulsive force PR[N] (> 0) and attractive force PA[N] (< 0) work as opposite forces (subscript, R: repulsion, A: aggregation). These resultant forces are shown in Equ.(Ⅰ-4). When the resultant force P < 0, the cohesive force acts so that the particles come closer to each other. If the resultant force P > 0, the dispersing force acts so that the particles move away.
The repulsive force PR is caused by the solution in which the hydrophobic colloid is dispersed, and when two colloidal particles having an electric double layer come close to each other, the osmotic pressure is generated due to the overlap of counterions in the electric double layer as shown in Fig.I-3. This is because the colloidal particles have a repulsive force.
On the other hand, the cause of the attractive force PA is that when the colloidal particles come close to each other, an interparticle attractive force due to the van der Waals force acts between the particles.
However, “aggregation or dispersion” in the particle system is determined by “stable or unstable” in the free energy of the system. Free energy V in a colloidal two-particle system is shown by the following equation as the sum of energies VR and VA caused by repulsive and attractive forces.
There is the following relation between the resultant force P(h) acting between two particles and the free energy of the system.
However, V(∞) = 0
Where, under the conditions of the electric double layer model described in detail in Ⅱ.Explantion(B), two charged particles with radius a[m] approach the particle interface distance h[m] from a distance, and the resultant force P(h) and free energy V(h) is approximately represented by the following equation.
V(h) = 2πaεΨo2exp(-κh) – aA/(12h) (Ⅰ-8)
κ2 = 2nz2e2/(εkT) (Ⅰ-9)
κ = 3.3 × 109z√C [/m] (at T = 298K) (Ⅰ-10)
In addition, in Equ.(Ⅰ-7) to Equ.(Ⅰ-10), Ψo: potential at the particle-water interface [V] , Ε: Dielectric constant of water (7.08 × 10-10[N/m2/C2], 25°C), A: Hamaker constant, z: valence of z-z type symmetric electrolyte, n (= n∞ = 1.0 × 103C): number of electrolyte ions in unit volume [1/m3], C: electrolyte concentration [mol/L].
(4) 疎水コロイドの凝集と分散
一般に系の自由エネルギーVの値が低いほど、その状態はより安定となる。2つの荷電粒子が接近したときの表面間距離 hに対する自由エネルギーV(h)と粒子間に働く合力P(h)の関係の事例を図Ⅰ-6に示す。
一般に、V(h)の極大値Vmax(dV(h)/dh = P(h) = 0 → PR = PA)が存在し、凝集系と分散系の境界にエネルギー障壁が現れる。粒子が接近したとき、「分散 → 凝集」へ移行するには、このエネルギー障壁を越える活性化エネルギーが必要となる。コロイド粒子はブラウン運動をしており、そのエネルギーはkT(= 26meV、25℃)を用いて議論される。Durhanによれば、半径100nm以上の粒子について、Vmax>15kTでは、ブラウン運動によってこの障壁を越える確率が極めて低く、長期間にわたってコロイド状態は安定に存在する。Vmax<15kTでは、この障壁を越える確率が高くなりコロイド系は不安定となり緩速凝集が進行し、さらにVmaxが消失すると急速凝集が起こることとなる。
(4) Aggregation and dispersion of hydrophobic colloids
Generally, the lower the free energy V of a system, the more stable its state. Figure I-6 shows an example of the relationship between the free energy V(h) and the resultant force P(h) acting between particles with respect to the surface distance h when two charged particles approach each other.
In general, there is a maximum value Vmax (dV(h)/dh = P(h) = 0 → PR = PA) of V(h), and an energy barrier appears at the boundary between the aggregating system and the dispersive system. When particles come close to each other, activation energy exceeding this energy barrier is required to shift from “dispersion to aggregation”. Colloidal particles are in Brownian motion, and their energy is discussed using kT (= 26meV, 25℃). According to Durhan, for particles with a radius greater than 100nm, Brownian motion has a very low probability of crossing this barrier at Vmax > 15kT, and the colloidal state is stable over a long period of time. When Vmax < 15 kT, the probability of crossing this barrier increases, the colloidal system becomes unstable, and slow aggregation progresses, and when Vmax disappears, rapid aggregation occurs.
本章での説明はコロイド状態の安定性をエネルギー的に論じているが、その状態が時間的にどの程度維持できるかについては、別の問題である。コロイドの凝集速度については、Ⅱ.解説(E)を参照されたい。
The discussion in this chapter energetically discusses the stability of the colloidal state, but another question is how long that state can be maintained over time. For the rate of colloid aggregation, see II. Explanation (E).
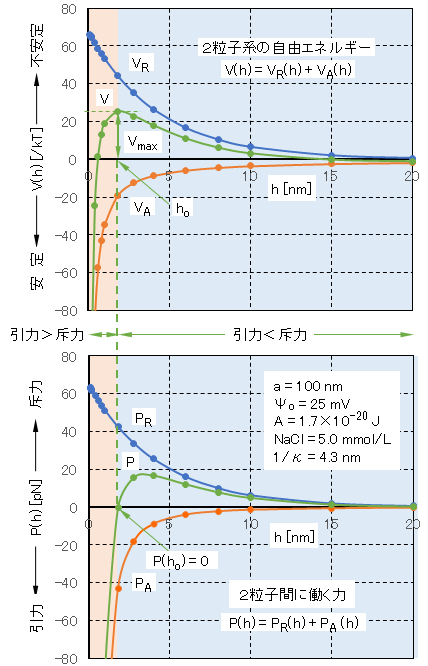
図Ⅰ-6 球形・同サイズ・同荷電の2粒子系に働く力と自由エネルギー
P:粒子間に働く合力、PR:静電気的反発力、PA:van der Waals引力、V:2粒子系の自由エネルギー{ただし、V(∞) = 0 とする}、VR:静電気的エネルギー、VA:van der Waalsエネルギー、
a:粒子半径、h:2粒子表面の最短距離、Ψo:表面電位(Stern電位)、A:Hamaker定数、1/κ:二重層の厚さ(Debye長さ)
Fig.I-6 Force and free energy acting on a two-particle system of spherical shape, same size, and same charge.
P: resultant force acting between particles, PR: electrostatic repulsion, PA: van der Waals attraction, V: free energy of two-particle system {however V (∞) = 0}, VR: electrostatic energy, VA: van der Waals energy,
a: particle radius, h: shortest distance between two particle surfaces, Ψo: surface potential (Stern potential), A: Hamaker constant, 1/κ: double layer thickness (Debye length).
学生や初心者の方は、同ファイルの各パラメータに具体的な数値を記入して、Vmaxは「どの因子によって大きく影響される」か実感されたい。そして、「その因子が変化する原因はどのような理由によるもの」か考察することが、現実の水浄化プロセスの開発・改善や維持管理において役立つこととなろう。
If you are a student or a beginner, please write a specific value for each parameter in the file so that you can feel what Vmax “is greatly affected by.” Then, it will be useful to consider “what is the cause of the change of the factor” in the development, improvement and maintenance of the actual water purification process.
3.2 コロイドの分散・凝集の因子
コロイド粒子が長時間にわたって安定であるか、凝集するかは、コロイド系の自由エネルギーの極大値Vmaxの高さに依存することを前節で述べた。ここでは、Vmaxの高さに及ぼす主な因子について述べる。Vmax (= V(ho))においては、P(ho) = 0であるので、式(Ⅰ-7)および式(Ⅰ-8)より、次式が得られる。
上式と式(Ⅰ-10)から、a = 一定、T = 一定のとき、Vmaxは、粒子界面の電位Ψoおよび電解質の電荷 zとその濃度Cに大きく依存することが分かる。
3.2 Factors for colloid dispersion/aggregation
It was stated in the previous section that whether the colloidal particles are stable or aggregate for a long time depends on the height of the maximum value Vmax of the free energy of the colloidal system. Here, the main factors affecting the height of Vmax are described. Since P(ho) = 0 at Vmax (= V(ho)), the following equation is obtained from Equ. (I-7) and Equ.(I-8).
From the above equation and Equ.(I-10), it is found that Vmax greatly depends on the potential Ψo of the particle interface, the electric charge z of the electrolyte and its concentration C when a = constant and T = constant.
(1) 粒子表面電位 Ψoとエネルギー障壁 Vmaxの高さ
界面電位Ψoを変化したときの、各Ψo値に対する自由エネルギーV(h)と距離 hの関係を図Ⅰ-7に示す。表面電荷が高くなると、Vmaxは高くなる。
Ψo<15mVでは Vmax<10kTとなり、ブラウン運動エネルギーによってエネルギー障壁を越える確率が高くなり、分散系は不安定で凝集が起こることが推定される。逆に、Ψo>25mVでは Vmax>40kTとなり、分散→凝集への活性化エネルギーが高く、凝集速度は極めて遅くなり分散系は安定であることが推定される。
(1) Particle surface potential Ψo and energy barrier Vmax height
Fig.I-7 shows the relationship between the free energy V(h) and the distance h for each value of Ψo when the interface potential Ψo is changed.
The higher the surface charge, the higher Vmax. When Ψo < 15mV, Vmax < 10kT, it is estimated that Brownian kinetic energy increases the probability of crossing the energy barrier and the dispersion system is unstable and aggregation occurs. On the other hand, when Ψo > 25mV, Vmax > 40kT, the activation energy from dispersion to aggregation is high, the aggregation rate is extremely slow, and it is estimated that the dispersion system is stable.
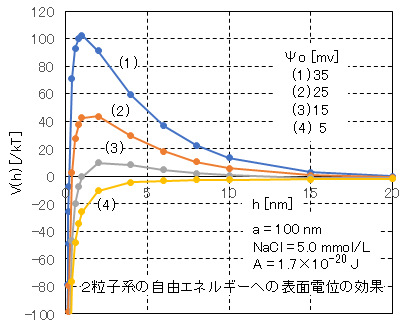
図Ⅰ-7 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する表面電位の効果
記号等の説明および計算については、図Ⅰ-6と同じ。
Fig.I-7 Effect of surface potential on free energy of spherical, same-sized, and same-charged two-particle system.
The explanation and calculation of symbols are the same as in Fig.I-6.
(2) 酸化物/水酸化物の表面の等電点
酸化物/水酸化物の固体粒子を水に分散させると、その表面は水和して、次の化学平衡を起こす。
-O-M=O(粒子表面)+ H2O → -(OH)-M-OH
-M-OH + H+ ⇄ -M-OH2+ (低pH)
-M-OH + OH– ⇄ -M-O– + H2O (高pH)
低pHでは水素イオンH+と、高pHでは水酸化物イオンOH–と粒子表面-M-OHとの平衡反応(不可逆的な化学吸着ではない)が生じ、正または負に帯電する。表面電荷が消失するpHoが高・低pHの中間で存在し、このpHo値を等電点(iso-electric point, iep)という。任意のpHにおける表面電位Ψoはネルンストの式から、次式で示される。
= – 59(pH – pHo) [mV] (at 25℃)
以上のことから、酸化物/水酸化物粒子の分散・凝集はpHに大きく依存することとなり、凝集操作においてpHは正確に調整する必要がある。表Ⅰ-4に、酸化物/水酸化物の表面の等電点を示すpHoを示す。
(2) Isoelectric point of oxide/hydroxide surface
When the oxide/hydroxide solid particles are dispersed in water, the surface hydrates and undergoes the following chemical equilibrium.
-M-OH + H+ ⇄ -M-OH2+ (low pH)
-M-OH + OH– ⇄ -M-O– + H2O (high pH)
Equilibrium reaction (not irreversible chemisorption) between hydrogen ion H+ at low pH and hydroxide ion OH– and particle surface-M-OH at high pH occurs, resulting in positive or negative charge. The pHo at which the surface charge disappears exists between high and low pH, and this pHo value is called the iso-electric point (iep). From the Nernst equation, the surface potential Ψo at any pH is given by the following equation.
= – 59(pH – pHo) [mV] (at 25℃)
From the above, the dispersion/aggregation of oxide/hydroxide particles largely depends on pH, and the pH must be adjusted accurately in the aggregation operation. Table I-4 shows pHo, which indicates the isoelectric point of the oxide/hydroxide surface.
Table I-4 Isoelectric point of oxide/hydroxide surface.
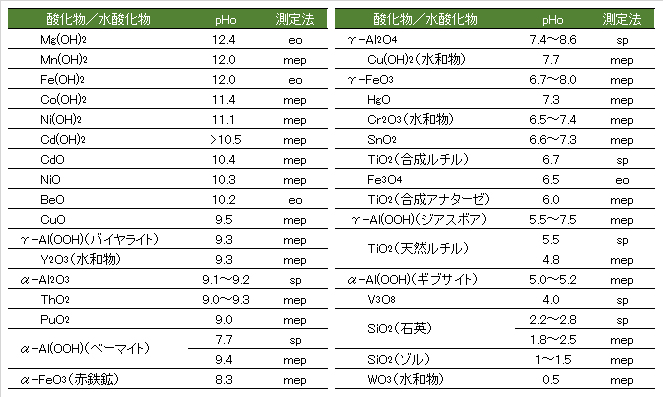
sp:流動電位法、eo:電気浸透法、mep:電気泳動法
文献(古澤, 2004)のデータをpHo値(測定方法によって、同じ物質でも値が異なるが)の順に並び替えた。
訂正:γ-Al2O4 → γ-Al2O3
sp: streaming potential method, eo: electroosmosis method, mep: electrophoresis method
The data in the literature (Furusawa, 2004) were sorted in the order of pHo values (though the same substance has different values depending on the measurement method).
Correction: γ-Al2O4 → γ-Al2O3
(3) 電解質添加によるエネルギー障壁の低下
前節で述べたように酸化物粒子などではpH調整により表面電荷を制御できるが、現実には溶液のpHを特定値に保つ必要もある。また、コロイド粒子間に働く van der Waals力の大きさは、コロイドを構成する内部の原子・分子に固有のもので粒子表面の性状に無関係であるので、溶液(分散媒)の条件によって変えることができない。
一方で、先に示した図Ⅰ-5・Dから分かるように、粒子・溶液界面の電気二重層が厚いほど、粒子同士が接近したときの重なり領域が広くなり、コロイド粒子間に働く反発力が増加する。
そこで、疎水コロイドが分散している溶液に電解質を加えると、上式(Ⅰ-10)で示したように、その濃度が高いほど、電気二重層の厚さ(1/κ)は小さくなり、粒子間の反発力は減少する。さらに添加する電解質イオンの価数zが大きくなると、その効果は格段に高くなる。
図Ⅰ-8に塩化ナトリムの添加によるエネルギー障壁Vmaxへの効果を示す。この事例では、NaCl濃度>100mmolでは、エネルギー障壁Vmax<15kTであるので、コロイド系は不安定となり、粒子の凝集が進行することが推定される。
なお、凝集に必要な電解質の濃度は、解離イオン価数zの6乗に反比例し、多価電解質の凝集効果が極めて効果的であることが実験により分かっているが、理論的にも説明できる(Ⅱ.解説(D)を参照)。
(3) Reduction of energy barrier by adding electrolytes
As described in the previous section, the surface charge of oxide particles can be controlled by adjusting the pH, but in reality it is also necessary to keep the pH of the solution at a specific value. Also, the magnitude of van der Waals force acting between colloidal particles is unique to the atoms and molecules inside the colloid and is not related to the properties of the particle surface, so it cannot be changed depending on the solution (dispersion medium) conditions.
On the other hand, as can be seen from Fig.I-5・D shown above, when the particles are close to each other, the thicker the electric double layer at the particle/solution interface, the wider the overlapping area and the repulsive force acting between the colloidal particles will increase.
Therefore, when an electrolyte is added to the solution in which the hydrophobic colloid is dispersed, as shown in the above Equ.(I-10), the higher the concentration, the smaller the thickness of electric double layer (1/κ), The repulsive force between particles is reduced. Further, when the valence z of the added electrolyte ion becomes large, the effect becomes remarkably high.
Fig.I-8 shows the effect of adding sodium chloride on the energy barrier Vmax. In this case, when the NaCl concentration> 100mmol, the energy barrier Vmax < 15kT, so it is presumed that the colloidal system becomes unstable and particle aggregation progresses.
The concentration of the electrolyte required for aggregation is inversely proportional to the sixth power of the dissociated ionic valence number z, and it is experimentally known that the aggregation effect of the polyvalent electrolyte is extremely effective, but it can be theoretically explained (See II. Explanation (D)).
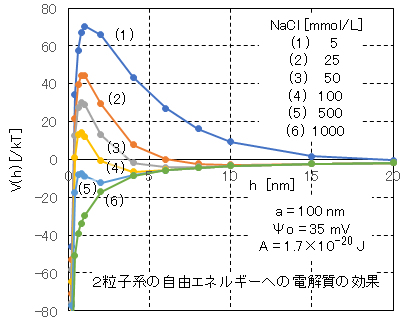
図Ⅰ-8 球形・同サイズ・同荷電の2粒子系の自由エネルギーに対する電解質の添加効果
記号等の説明および計算については、図Ⅰ-6と同じ。
Fig.I-8 Effect of addition of electrolyte on free energy of spherical, same size and same charged two particles system.
The explanation and calculation of symbols are the same as in Fig.I-6.
4.親水コロイドの塩析
親水コロイドのコロイド粒子表面には、親水性の官能基(-OHや-COOH、-CO-、-NH2など)を多数有している。上記図Ⅰ-4に示したように、これらの親水基が水素結合によって水分子を粒子表面に強く引き付けているために、水和水層が立体障害になってコロイド粒子同士の凝集は妨げられている。したがって、親水コロイドを凝集させるためには、表面での水素結合を切り、コロイド粒子を覆っている水和水を表面から剥ぎ取らなければならない。
電解質をコロイド溶液に加えると、水中でイオンに電離する。これらの電離イオンは、親水基よりも強く水分子と引き合うので、親水コロイドに塩化ナトリウム NaClなどの塩を加えれば、理論上は水和水を失って、親水コロイドは沈殿するはずである。しかし、NaCl濃度を1mol/Lぐらいにしても、なかなかコロイド粒子は沈殿しない。水溶液には約1000/18 ≒ 56mol/Lの水分子が存在為ているのに対して、塩濃度が1mol/L程度ではイオンの数が少なすぎて、親水基と水分子の水素結合を切るに至らない。親水コロイドについては、少量の塩を加えただけでは凝集が起こらず、NaCl濃度が5~10mol/Lぐらいになって、初めて親水基と水分子の水素結合が切れ、親水コロイドの凝集が起こる。このように親水コロイドに多量の電解質を加えて凝集させることを、一般的に塩析(salting out)という。
セッケンのコロイド溶液に飽和食塩水を加えてセッケンを析出させたり、タンパク質のコロイド溶液である豆乳にニガリMgCl2や硫酸カルシウムCaSO4を加えて豆腐を作るのは、塩析を利用したものである。
4. Hydrocolloid salting out
The surface of the colloidal particles of the hydrocolloid has a large number of hydrophilic functional groups (-OH, -COOH, -CO-, -NH2, etc.). As shown in Fig.I-4 above, because these hydrophilic groups strongly attract water molecules to the particle surface through hydrogen bonds, the hydration water layer becomes a steric hindrance and prevents the aggregation of colloid particles. Therefore, in order to agglomerate the hydrocolloid, it is necessary to break the hydrogen bonds on the surface and strip the hydration water covering the colloid particles from the surface.
When an electrolyte is added to a colloidal solution, it ionizes in water. Since these ionized ions attract water molecules more strongly than hydrophilic groups, if a salt such as sodium chloride NaCl is added to the hydrocolloid, theoretically the hydration water should be lost and the hydrocolloid should precipitate. However, even if the NaCl concentration is about 1mol/L, the colloidal particles do not precipitate easily. About 1000/18 ≈ 56mol/L of water molecules exist in the aqueous solution, whereas at salt concentration of about 1mol/L, the number of ions is too small to cut the hydrogen bond between the hydrophilic group and water molecule. Does not reach. With respect to the hydrocolloid, aggregation does not occur even if a small amount of salt is added, and the hydrogen bond between the hydrophilic group and the water molecule is broken only when the NaCl concentration reaches about 5 to 10 mol/L, and aggregation of the hydrocolloid occurs. In this way, adding a large amount of electrolyte to the hydrocolloid to cause aggregation is generally referred to as salting out.
Salting out is used to make tofu by adding saturated saline to a colloidal solution of soap to precipitate soap, or to add soymilk, which is a colloidal solution of protein, to bittern MgCl2 and calcium sulfate CaSO4.
(1) 保護コロイド
疎水コロイドに親水コロイドを加えると、疎水コロイドが凝析しにくくなることがある。このときに加える親水コロイドを保護コロイド(protective colloid)という。
これは、疎水コロイドの周りを親水性の保護コロイドが取り囲み、さらにその周りを水分子が水和しているため、疎水コロイドの表面が親水化されるからである。保護コロイドを加えると、疎水コロイドは電解質に対して安定になる。例えば、疎水性である赤色アルカリ性金コロイドに対して、ゼラチンは強い保護作用を示す。その他の例としては、墨汁のニカワやマヨネーズの卵黄は、代表的な保護コロイドである。ただし、この保護作用の強さは物質の種類だけでなく、pHや調整法などにより著しい影響を受ける。
(1) Protective colloid
When a hydrophilic colloid is added to the hydrophobic colloid, the hydrophobic colloid may be difficult to coagulate. The hydrocolloid added at this time is called a protective colloid.
This is because the hydrophilic protective colloid surrounds the hydrophobic colloid and the water molecules are hydrated around it, so that the surface of the hydrophobic colloid is hydrophilized. The addition of protective colloid makes the hydrophobic colloid stable to the electrolyte. For example, gelatin has a strong protective action against red alkaline gold colloid, which is hydrophobic. As another example, the ink sticker and the mayonnaise egg yolk are typical protective colloids. However, the strength of this protective effect is significantly affected not only by the type of substance, but also by pH and adjustment method.
5.会合コロイドとミセル
界面活性剤は、生活・産業において広く活用されている。水浄化においても、懸濁水の凝集剤として利用されている。詳しくは、Ⅱ.解説(G)に記載しているが、ここではその代表的な性質を概説する。
5. Association colloids and micelles
Surfactants are widely used in daily life and industry. It is also used as a coagulant for suspended water in water purification. Although it is described in II.Explanation (G) for details, its typical properties are outlined here.
5.1 界面活性剤とミセル
ミセル(micelle)とは、界面活性剤の分子またはイオンの集合体のことである。界面活性剤は、分子内に親水基と疎水基の両方を持つため、両親媒性分子とも呼ばれる。次の図Ⅰ-9に代表的な界面活性剤であるステアリン酸ナトリウムC17H35COONaの構造式を示す。
5.1 Surfactants and micelles
A micelle is an aggregate of surfactant molecules or ions. Since the surfactant has both a hydrophilic group and a hydrophobic group in the molecule, it is also called an amphipathic molecule. Fig.I-9 below shows the structural formula of a typical surfactant, sodium stearate C17H35COONa.
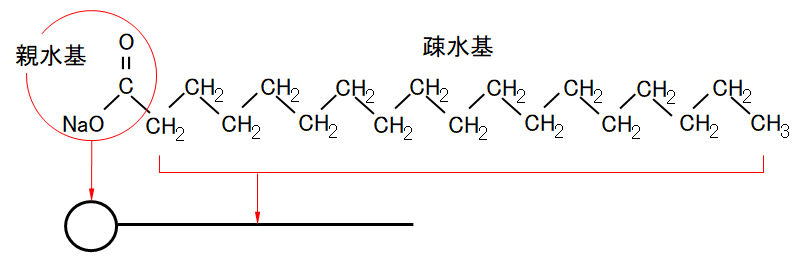
図Ⅰ-9 ステアリン酸ナトリウムC17H35COONaの構造式と略号
Fig.I-9 Structural formula and abbreviations for sodium stearate C17H35COONa
界面活性剤分子は分子内に疎水基があるため、水中では不安定である。水はその分子間の凝集力が大きいため、疎水基を水からはじき出そうとする傾向がある。図Ⅰ-10・Aのように、少量添加した界面活性剤の大半は、空気-水界面へ移動し疎水基を空気側へ向けて配置される。また、水と油のような状況でも、界面活性剤はその界面へと移動・配置される。界面活性剤の界面吸着能はその重要な物性の1つである。界面活性剤がミセルを形成し始める濃度を臨界ミセル濃度(critical micellar concentration、cmc)といい、この濃度は、コロイドであるかないかを区別する重要な値である。
水溶液中の界面活性剤の濃度を上げていき、cmcに達すると、それ以上は界面に存在できない状態となる。この状態は、溶液の表面全体が界面活性剤分子で覆われ、図Ⅰ-10・Bのように、表面配置が飽和してしまった状態である。さらに濃度上げていくと、行き場のなくなった界面活性剤は分子同士で疎水基を重ね合わせ、親水基を外側(水側)に向けて互いに集まることにより、図Ⅰ-10・Cのように安定な集合体を形成して水中に分散する。この集合体がミセルである。
Surfactant molecules are unstable in water because they have a hydrophobic group in the molecule. Since water has a large cohesive force between its molecules, it tends to push out hydrophobic groups from water. As shown in Fig.I-10・A, most of the surfactants added in small amounts move to the air-water interface and are arranged with the hydrophobic groups facing the air. Moreover, even in a situation such as water and oil, the surfactant moves and is arranged at the interface. The interfacial adsorption capacity of surfactants is one of its important physical properties. The concentration at which the surfactant begins to form micelles is called the critical micellar concentration (cmc), and this concentration is an important value for distinguishing whether or not it is a colloid.
When the concentration of the surfactant in the aqueous solution is increased to reach cmc, it becomes impossible to exist at the interface any further. In this state, the entire surface of the solution is covered with surfactant molecules, and the surface arrangement is saturated, as shown in Fig.I-10・B. When the concentration is further increased, the surfactant, which has no place to go, becomes stable as shown in Fig.I-10・C by superimposing hydrophobic groups on the molecules and gathering hydrophilic groups toward the outside (water side). It forms various aggregates and disperses in water. This aggregate is a micelle.
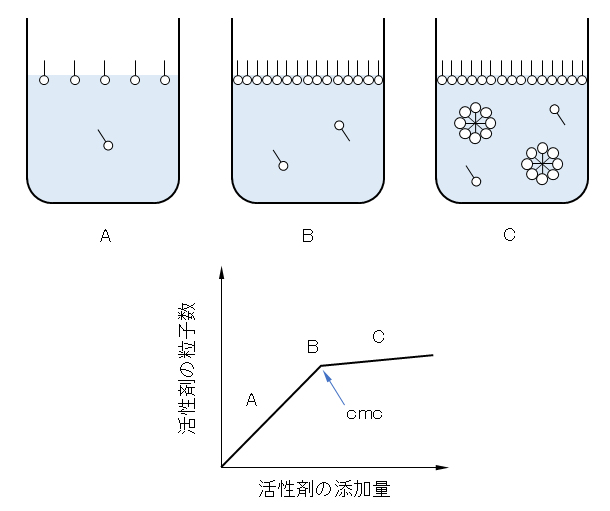
図Ⅰ-10 界面活性剤の添加量とその水中での存在状態
cmc:臨界ミセル濃度
Fig.Ⅰ-10 Amount of surfactant added and its presence in water.
cmc: Critical micelle concentration.
5.2 不溶性物質の可溶化
界面活性剤を使うと、水と油のように互いに混ざり合わない物質の一方を、他方に分散させることもできる。これは、界面活性剤がミセルを形成して、ミセル内にその物質が取り込まれるからである。図Ⅰ-11・Aは、ミセル内に油相が取り込まれ、水中に油が分散している事例である。液体に溶けにくい物質が界面活性剤の存在下でその液体に溶けるようになる現象を可溶化(solubilization)という。
界面活性剤溶液への可溶化は、臨界ミセル濃度以上で起こる。この場合の可溶化量と界面活性剤の濃度との間には、一般的に図Ⅰ-11・Bのような関係がある。このグラフから、逆に臨界ミセル濃度を間接的に求めることもできる。
5.2 Solubilization of insoluble substances
Surfactants can also be used to disperse one of the immiscible substances, such as water and oil, in the other. This is because the surfactant forms micelles and the substance is taken into the micelles. Fig.I-11・A is an example in which the oil phase is taken into the micelle and the oil is dispersed in water. The phenomenon in which a substance that is difficult to dissolve in a liquid becomes soluble in the liquid in the presence of a surfactant is called solubilization.
Solubilization in a surfactant solution occurs above the critical micelle concentration. In this case, there is generally a relationship between the amount of solubilization and the concentration of surfactant as shown in Fig.I-11・B. Conversely, the critical micelle concentration can be indirectly determined from this graph.
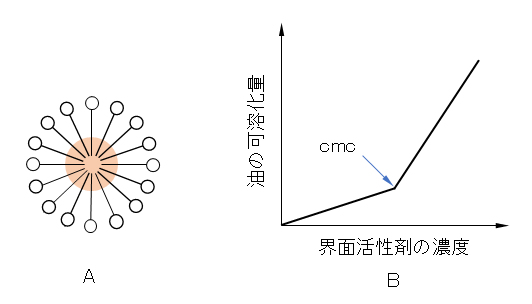
図Ⅰ-11 界面活性剤の添加による油性物質の水中への可溶化
A:O/Wマイクロエマルジョンのモデル(●:油の粒子)、B:界面活性剤の濃度と油の可溶化量
Fig.I-11 Solubilization of oily substances in water by adding a surfactant.
A: O/W microemulsion model (●: oil particles), B: surfactant concentration and oil solubilization amount.
可溶化量が増すと、ミセルは膨らんでいく。光の散乱状態は、ミセルが膨らむと増大し、液は半透明になって乳光を発したり、やや濁って見えたりする。そこで、この現象を界面活性剤の乳化作用(emulsifying action)という。マヨネーズや乳液などには界面活性剤が使われており、この乳化作用のために、白く濁って見える。
前述した水-油-界面活性剤の3成分系であるが、この系に中級アルコール(炭素数4~8)を補助剤として添加し4成分系にすると、図Ⅰ-12に示すように、水に対して多量の油を(O/W)、または、油に対して多量の水(W/O)を含む広い組成範囲のエマルジョンをつくることができる。
The micelles swell as the amount of solubilization increases. The scattering state of light increases as the micelle swells, and the liquid becomes translucent and emits opalescence, or appears slightly cloudy. Therefore, this phenomenon is called an emulsifying action of the surfactant. Surfactants are used in mayonnaise and milky lotion, and due to this emulsifying action, they appear white and turbid.
It is a water-oil-surfactant three-component system described above, but if a medium alcohol (4 to 8 carbon atoms) is added as an auxiliary agent to this system to make a four-component system, as shown in Fig.I-12, It is possible to prepare an emulsion having a wide composition range containing a large amount of oil with respect to water (O/W) or a large amount of water with respect to oil (W/O).
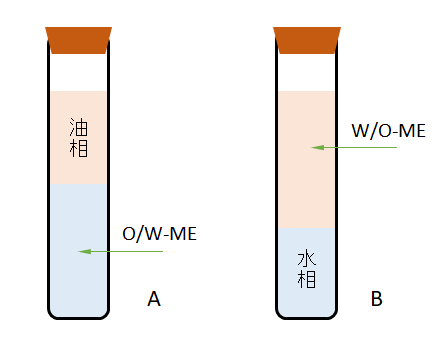
図Ⅰ-12 オクチル硫酸ナトリム-ヘキサノール-デカン-食塩水の4成分系でのマイクロエマルジョン(ME)の生成
Fig.I-12 Generation of microemulsion (ME) in a four-component system of sodium octyl sulfate-hexanol-decane-saline.
6.コロイド溶液の物性
6.1 透析
コロイド粒子は、ろ紙の穴より小さいので、ろ紙を素通りして分離できない。しかし、セロハン膜やコロジオン膜の穴よりは大きいので、これらの半透膜を通過できない。一方で、コロイド粒子より小さなイオンや分子は、このセロハン膜の穴をも通ることができる。そこで、このような装置を使うことで、小さなイオンや分子を除き、コロイド粒子のみの溶液にすることが可能となる。この操作を透析(dialysis)という。
透析を利用した水酸化鉄(III)・Fe(OH)3のコロイド溶液の作成を説明する。沸騰水に塩化鉄(III)・FeCl3水溶液を加えると、加水分解反応が起こり、赤褐色のFe(OH)3のコロイド溶液が作成できる。沸騰水での反応の理由は、高温のために加水分解反応が急激に進むので、多数に生成したFe(OH)3の小さな結晶核が大きな沈殿粒子まで成長できず、コロイド粒子のサイズで成長が停止しているからである。このコロイドは、溶液中の水素イオン・H+または鉄(III)イオン・Fe3+が表面に吸着しているので、正に帯電した疎水コロイドとなっている。
生じたコロイド溶液を半透膜であるセロハン袋に入れて、流水中に浸して透析を行うと、水素イオン・H+や塩化物イオン・Cl–は拡散によりセロハン膜を通過して流出していく。しかし、Fe(OH)3のコロイド粒子は半透膜を通過できず、セロハン膜内に留まる。この操作によって、Fe(OH)3のコロイドをセロハン袋中に精製することができる。
6. Physical properties of colloidal solution
6.1 dialysis
Since the colloidal particles are smaller than the holes in the filter paper, they cannot be separated by passing through the filter paper. However, since it is larger than the holes in the cellophane membrane or collodion membrane, it cannot pass through these semipermeable membranes. On the other hand, ions and molecules smaller than the colloidal particles can also pass through the holes in this cellophane film. Therefore, by using such an apparatus, it becomes possible to remove small ions and molecules and form a solution containing only colloidal particles. This operation is called dialysis.
The preparation of a colloidal solution of iron(III) hydroxide/Fe(OH)3 using dialysis will be described. When iron(III) chloride/FeCl3 aqueous solution is added to boiling water, a hydrolysis reaction occurs and a reddish brown colloidal solution of Fe(OH)3 can be prepared. The reason for the reaction in boiling water is that the hydrolysis reaction rapidly progresses due to the high temperature, so that many small crystal nuclei of Fe(OH)3 formed in large numbers cannot grow into large precipitated particles. , Because the growth has stopped at the size of the colloidal particles. This colloid has hydrogen ions, H+ or iron(III) ions, Fe3+ in the solution adsorbed on the surface, so it is a colloid having a positively charged hydrophobicity.
When the resulting colloidal solution is put in a cellophane bag that is a semipermeable membrane and immersed in running water for dialysis, hydrogen ions H+ and chloride ions Cl– flow out through the cellophane membrane due to diffusion. However, Fe(OH)3 colloidal particles cannot pass through the semipermeable membrane and remain in the cellophane membrane. By this operation, the Fe(OH)3 colloid can be purified in the cellophane bag.


Photo I-1 (Left) Reddish brown iron(III) hydroxide/Fe(OH)3 colloidal solution. (Right) Purification of iron(III) hydroxide using cellophane membrane.
出典(Source):http://www.hyogo-c.ed.jp/~rikagaku/jjmanual/jikken/kaga/kaga18.htm
透析を有効に利用しているのが、私たちの体の中にある腎臓である。腎臓には、血液中に含まれる尿素(NH2)2COなどの老廃物を取り除く働きがある。腎臓病により、腎臓の機能が低下してくると、老廃物を体外に排泄できなくなり、尿毒症により生命の危機に陥ることとなる。これを回避するために、人工透析が行われる。人工透析には、図Ⅰ-13に示すような血漿分離器が用いられている。
まず、体外に取り出した血液を血漿分離器に通して、血球成分と血漿成分に分離する。赤血球や白血球などの血球成分は透析膜を通過できないが、小さい分子である尿素(NH2)2COは透析膜を通過するので、これらを分離することができる。このとき分離された血漿の代わりに、新鮮な血漿もしくはアルブミン溶液を補充する。
人工透析は、半透膜としての作用が弱った腎臓の働きを、このようにして人工的に行う治療法である。
The effective use of dialysis is the kidneys in our body. The kidney has a function of removing waste products such as urea (NH2)2CO contained in blood. When kidney function deteriorates due to kidney disease, waste products cannot be excreted outside the body and uremia causes a life threat. To avoid this, artificial dialysis is performed. For artificial dialysis, a plasma separator as shown in Fig.I-13 is used.
First, the blood taken out of the body is passed through a plasma separator to separate it into blood cell components and plasma components. Blood cell components such as red blood cells and white blood cells cannot pass through the dialysis membrane, but urea (NH2)2CO, which is a small molecule, passes through the dialysis membrane. Can be separated. At this time, instead of the separated plasma, fresh plasma or albumin solution is supplemented.
Artificial dialysis is a therapeutic method in which the function of the kidney, which has weakened the action as a semipermeable membrane, is artificially performed in this manner.
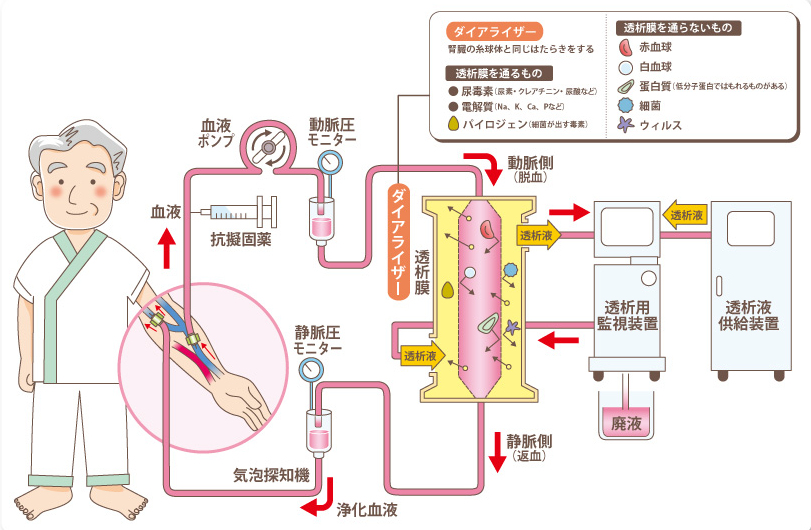
図Ⅰ-13 血液透析の原理
Fig.I-13 Hemodialysis principle
出典(Source):http://www.twmu.ac.jp/NEP/touseki/touseki-genri.html
6.2 光学的性質
コロイドは必ずしも濁っているとは限らず、透明または半透明なものも多い。しかし、透明に見えていても、コロイドの横から強い光を当てると、光の通路が光って見える。これは、コロイド粒子の大きさが可視光の波長(350~700nm)とほぼ等しいため、その表面で光がよく散乱されるからである。この現象をチンダル(Tyndall)現象といい、この光をチンダル(Tyndall)光という。これはコロイドの特性の1つであり、チンダル現象の有無により、コロイドを見分けることが可能となる。
着色物質は光を吸収する。吸収の極大波長は分子・イオン・結晶では、物質に固有なもので、それぞれ固有な色を呈している。しかし、コロイドの色は物質に固有なものではない。
光の散乱と吸収の度合いを一つにまとめると、
ここで、Io/I は入射光/透過光の強さ、l は測定セルの厚さ、ε/τ は吸収係数/濁度である。ε = 0 のときにThydall式、τ = 0 のときにLambert式となる。測定セル中のコロイド粒子数をN、粒子半径をaとすると、
ε = πNa2QA τ = πNa2QS (Ⅰ-13)
となる。QA/QSは吸収因子/散乱因子といわれ、粒子半径 a、測定波長λ、屈曲率などの関数である。
粒子による散乱には、レイリー(Rayleigh)散乱とミー(Mie)散乱がある。レイリー散乱は、光の波長よりも小さいサイズの粒子による散乱現象である。ミー散乱は、光の波長程度のサイズの粒子による散乱現象である。粒子のサイズが大きくなるとミー散乱と幾何光学の双方の手法による計算結果が類似するようになる。
散乱波の波長λと散乱粒子の直径 d(= 2a)に関するサイズパラメータとして、
があり、α≪1 はレイリー散乱、α~1 はミー散乱、α≫1 は幾何光学近似で表現できる。
6.2 Optical properties
Colloids are not always cloudy and are often transparent or translucent. However, even if it looks transparent, the passage of light appears to shine when strong light is applied from the side of the colloid. This is because the size of the colloidal particles is almost equal to the wavelength of visible light (350 to 700 nm), so that light is well scattered on the surface. This phenomenon is called Tyndall phenomenon, and this light is called Tyndall light. This is one of the characteristics of colloids, and it is possible to distinguish colloids by the presence or absence of the Tyndall phenomenon.
The coloring substance absorbs light. The maximum absorption wavelength is unique to a substance in molecules, ions, and crystals, and each has a unique color. However, the color of the colloid is not unique to the substance.
To summarize the degree of light scattering and absorption,
Here, Io/I is the intensity of incident light/transmitted light, l is the thickness of the measuring cell, and ε/τ is the absorption coefficient/turbidity. When ε = 0, the Thydall formula is obtained, and when τ = 0, the Lambert formula is obtained. If the number of colloidal particles in the measuring cell is N and the particle radius is a,
Here, QA/QS is called absorption factor/scattering factor, and is a function of particle radius a, measurement wavelength λ, bending ratio, and the like.
The scattering by particles includes Rayleigh scattering and Mie scattering. Rayleigh scattering is a scattering phenomenon caused by particles having a size smaller than the wavelength of light. Mie scattering is a scattering phenomenon due to particles having a size about the wavelength of light. The larger the particle size, the more similar the calculation results by both Mie scattering and geometric optics.
As a size parameter for the wavelength λ of the scattered wave and the diameter d (= 2a) of the scattering particle,
α<< 1 can be expressed by Rayleigh scattering, α~1 can be expressed by Mie scattering, and α >> 1 can be expressed by geometrical optics approximation.


Photo I-2 Examples of the Tyndall phenomena.
出典(Source):(左, left)https://cdn.pixabay.com/photo/2014/11/21/14/01/sunbeam-540589_640.jpg
出典(Source):(右, right)https://blogs.yahoo.co.jp/chemy1i/GALLERY/show_image.html?id=36617748&no=1
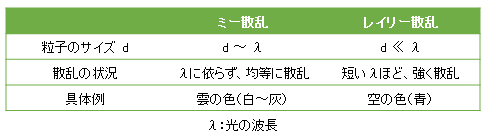
チンダル現象は、主にミー散乱によるものが大きい。レイリー散乱は、光の波長の依存性が高く、波長の短い青色の光は、赤色の光よりも強く散乱される。長い波長の光は粒子による散乱が少なく、波長の短い光ほど粒子にょる散乱が起きやすい性質がある。空が青いのは、レイリー散乱より説明できる。これは、大気中の微粒子により、青色の光が強く散乱されるからである。また、ミー散乱は、波長の依存性が低いので、どの波長の光も同程度に散乱する。雲が白く見えるのは、ミー散乱が原因である。
The Tyndall phenomenon is mainly due to Mie scattering. Rayleigh scattering is highly dependent on the wavelength of light, and blue light having a short wavelength is scattered more strongly than red light. Light with a long wavelength is less scattered by particles, and light with a shorter wavelength is more likely to be scattered by particles. The blue sky can be explained by Rayleigh scattering. This is because blue light is strongly scattered by the fine particles in the atmosphere. Since Mie scattering has low wavelength dependence, light of any wavelength scatters to the same extent. Clouds appear white due to Mie scattering.
Table I-5 Difference between Mie scattering and Rayleigh scattering.
6.3 微粒子の運動
微粒子は、その密度が媒質のそれよりも大きい場合、重力による下降運動するとともに、熱運動としてのブラウン運動も行っている。この両運動の兼ね合いで、粒子全体としての運動が決まる。
6.3 Movement of fine particles
If the density of the particles is higher than that of the medium, the particles move downward due to gravity and also perform Brownian motion as thermal motion. The balance of these two movements determines the movement of the particle as a whole.
(1) 沈降
重力 Fgで下降する場合には、媒質から抵抗 Ffを受ける。上下方向の流れがない媒質中では、FgとFfがつり合うと粒子は等速 uで下降し、これを沈降という。
粒子の半径 aの球とすると、浮力を補正した重力は、
ρ・ρo:粒子・媒質の密度、g:重力加速度
抵抗力は媒質の摩擦抵抗で、摩擦抵抗をf、下降速度を uとすると、
球状粒子は剛体でその濃度が希薄な場合(自由沈降)には、媒質の粘度をηとすると、
Fg = Ffの場合には、上記3式の関係より、下降速度 uは次式で示される。これをStokesの式という。
なお、高速回転で遠心力を利用する場合には、重力加速度 g → 遠心力の加速度 ω2x(ω:角速度、x:回転中心から粒子までの距離)を用いる。この方法は小さい粒子の沈降・分離に用いられる。
(1) Sedimentation
When descending due to gravity Fg, it receives resistance Ff from the medium. In a medium with no vertical flow, when Fg and Ff are balanced, the particles descend at a constant velocity u, which is called sedimentation.
Assuming a sphere with a particle radius of a, the gravity with buoyancy corrected is
ρ/ρo: density of particle/medium, g: gravitational acceleration.
The resistance force is the frictional resistance of the medium. If the frictional resistance is f and the descending speed is u,
If spherical particles are rigid and their concentration is low (free sedimentation), let the viscosity of the medium be η,
In the case of Fg = Ff, the descending speed u is shown by the following equation from the relation of the above three equations. This is called Stokes’ formula.
When using centrifugal force at high speed, use gravitational acceleration g → centrifugal force acceleration ω2x (ω: angular velocity, x: distance from the center of rotation to the particle). This method is used for sedimentation and separation of small particles.
(2) ブラウン運動
イギリスの植物学者であるRobert Brownは、1827年に植物の花粉から生じた微粒子が、不規則な運動をすることを発見した。しかし、発見当時、この現象は「花粉の生命力に基づくものである」と誤解されていた。Brownは、これをブラウン運動(Brownian motion)と名付けた。その後、他の微細な粒子でも、同様の現象が起こることが確認されたが、長い間その原因は不明のままであった。
1905年に相対性理論で有名なAlbert Einsteinが、ブラウン運動の原因を突き止めた。Einsteinは、熱運動する媒質分子の不規則な衝突により、ブラウン運動が引き起こされるということを、統計力学を駆使して理論的に説明した。媒質に浮かぶ微粒子は、各瞬間毎に非常に多くの媒質分子に衝突されているが、その衝突はデタラメに起こるので、ある瞬間に微粒子が受け取る運動量はつり合っていない。この衝突の不均衡のために、粒子が動くのである。
ブラウン運動は粒子の不規則な熱運動であるから、統計的に計算できる。時間 tで z軸方向へ動く距離の平均
ここで、D は粒子の拡散係数である。これをEinsteinのブラウン運動という。さらに、Einsteinによると、
f は摩擦係数で、前節<沈降>の式(3)を用いて、次に示すEinstein-Stakesの式が得られる。
これを式(1)に代入すると、
が得られる。
ブラウン運動による粒子の移動は、粒子の個数濃度の濃い方から希薄な方へと起こる。上式によると、ブラウン運動による拡散の速さは、粒径 aが小さいほど速く、また粒子の平均速度 <x>はボルツマン分布に従い、温度 Tが高いほど拡散は速くなる。
(2) Brown movement
In 1827, British botanist Robert Brown discovered that the particles produced by plant pollen had irregular movements. However, at the time of discovery, this phenomenon was misunderstood as “based on the vitality of pollen.” Brown termed this Brownian motion. After that, the same phenomenon was confirmed to occur with other fine particles, but the cause remained unknown for a long time.
In 1905, Albert Einstein, famous for the theory of relativity, discovered the cause of the Brownian movement. Einstein theoretically explained, using statistical mechanics, that Brownian motion is caused by irregular collisions of thermally moving medium molecules. The particles floating in the medium are collided with a large number of molecules of the medium at each moment, but since the collisions occur randomly, the momentums the particles receive at a certain moment are not balanced. This imbalance of collisions causes the particles to move.
The Brownian motion is an irregular thermal motion of particles and can be calculated statistically. The average distance moved in the z-axis direction at time t is
Where D is the diffusion coefficient of the particles. This is called Einstein’s Brownian movement. Furthermore, according to Einstein,
f is the coefficient of friction, and the following Einstein-Stakes equation can be obtained by using Equ.(3) in the previous section.
Substituting this into Equ.(1),
is obtained.
Substituting this into Equ.(1),
is obtained.
Movement of particles due to Brownian motion occurs from the one with a high number concentration of particles to the one with a low number concentration. According to the above equation, the smaller the particle size a, the faster the diffusion speed due to Brownian motion, the average velocity <x> of the particles follows the Boltzmann distribution, and the higher the temperature T, the faster the diffusion.
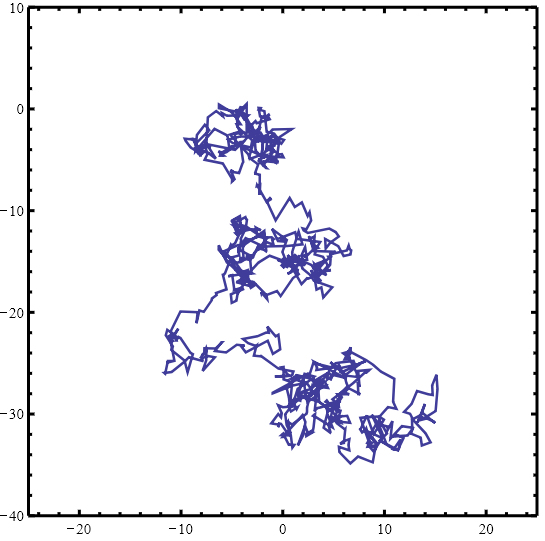
図Ⅰ-14 ブラウン運動のシミュレーションと動画
(図をクリックすると動画サイトにリンクする)
Fig.I-14 Brownian motion simulation and video
(Click the figure to link to the video site.).
出典(Source):https://ja.wikipedia.org/wiki/%E3%83%96%E3%83%A9%E3%82%A6%E3%83%B3%E9%81%8B%E5%8B%95
(3) ブラウン運動と沈降
泥水のようなコロイドにおいて、泥の微粒子がなかなか沈降してこないのは、微粒子がブラウン運動をしているからである。重力によって微粒子が沈降しても、ブラウン運動によって、微粒子は希薄になった上部へと拡散する。コロイド粒子が沈降して下部に沈積してしまうか、液中に浮遊しているかどうかは、媒質の粘度にもよるが、主として粒径に依存する。粒径が大きいものは沈降して、粒径が小さいものは拡散する。
式Ⅰ-14と式Ⅰ-16から計算した、水中における球形粒子(ρ/ρo = 2.5)のブラウン運動と重力沈降の比較を図Ⅰ-15に示す。粒子半径が100nm付近(ao)で、移動距離と沈降速度が等しくなる。粒子径 a≪aoではブラウン運動が支配的となって粒子の分散状態が継続し、a≫aoでは粒子は沈降することとなる。
a = 1μmレベルの粒子の沈降速度は3.6μm/sとなり、1mの深さに沈殿するのに3.2日を要する。上下左右の流れのある国内河川では、雨天時の泥水を構成する微細な粒子は沈降することなく海に流れ込むこととなる。
(3) Brownian motion and Sedimentation
In colloids such as muddy water, the fine particles of mud do not settle down easily because they are in Brownian motion. Even if the particles settle due to gravity, the Brownian motion causes the particles to diffuse to the diluted upper part. Whether the colloidal particles settle and deposit in the lower part or whether they are suspended in the liquid depends mainly on the particle size, although it depends on the viscosity of the medium. Those with a large particle size settle and those with a small particle size diffuse.
Fig.I-15 shows a comparison between Brownian motion of spherical particles (ρ/ρo = 2.5) in water and gravity settling calculated from Equ.(I-14) and Equ.(I-16). When the particle radius is around 100nm (ao), the moving distance and the sedimentation velocity become equal. When the particle size is a << ao, Brownian motion becomes dominant and the dispersed state of particles continues, and when a >> ao, the particles settle.
The sedimentation velocity of particles at a = 1μm level is 3.6μm/s, and it takes 3.2 days to sediment at a depth of 1m. In domestic rivers that flow vertically and horizontally, the fine particles that make up mud during rain will flow into the sea without settling.
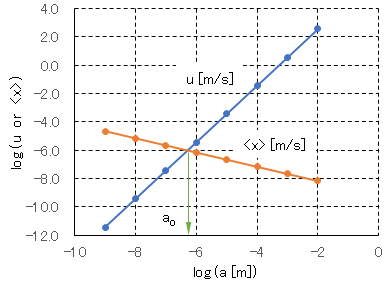
図Ⅰ-15 水中における球形粒子のブラウン運動と重力沈降の比較
a:粒子の半径[nm]、u:重力による沈降速度[m/s]、<x>:ブラウン運動による平均移動距離[m/s]
Fig.I-15 Comparison of Brownian motion of spherical particles in water and gravity settling.
a: radius of particle [nm], u: sedimentation velocity due to gravity [m/s], <x>: average travel distance due to Brownian motion [m/s].
T = 298[K], ρo = 9.97 x 102 [kg/m3], η = 8.94 x 10-4 [kg/m/s], ρ/ρo = 2.5, k = 1.38×10-23[J/K], g = 9.78[m/s2].
6.4 電気泳動
表面が正あるいは負に帯電しているコロイド粒子は、電極を入れて電圧をかけると、表面電荷と反対符号の極へと移動する。これを電気泳動(electrophoresis)という。この現象から、コロイド粒子の表面が、正負どちらに帯電しているのかが決定できる。
例えば、水酸化鉄(Ⅲ)・Fe(OH)3コロイド溶液を電気泳動させると、Fe(OH)3のコロイド粒子は、ゆっくりと陰極の方へ移動するので、Fe(OH)3のコロイド粒子は、正に帯電していることが分かる。一般に正に帯電しているコロイド粒子を含むコロイドを正コロイド(positive colloid)、負に帯電しているコロイド粒子を含むコロイドを負コロイド(negative colloid)という。
粒子の移動は、粒子の大きさや形状、表面電荷、加えた電圧、pH、温度などによって影響され、異なるコロイド粒子を、移動速度の差を使って分離することもできる。これは、タンパク質・DNA断片の分離・分析などによく用いられる。なお、疎水コロイドの電気泳動の移動速度は比較的大きいが、親水コロイドは水和水のために、移動速度は小さい。
6.4 Electrophoresis
Colloidal particles whose surface is positively or negatively charged move to a pole having the opposite sign to the surface charge when an electrode is applied and a voltage is applied. This is called electrophoresis. From this phenomenon, it can be determined whether the surface of the colloidal particles is positively or negatively charged.
For example, when iron(III) hydroxide/Fe(OH)3 colloidal solution is electrophoresed, the Fe(OH)3 colloidal particles slowly grow into the cathode. It is understood that the Fe(OH)3 colloidal particles are positively charged as they move in the direction. Generally, a colloid containing positively charged colloidal particles is positive colloid, and a colloid containing negatively charged colloidal particles is negative colloid.
The movement of particles is affected by the size and shape of particles, surface charge, applied voltage, pH, temperature, etc., and different colloidal particles can also be separated using the difference in moving speed. It is often used for the separation and analysis of proteins and DNA fragments. The migration speed of electrophoresis of the hydrophobic colloid is relatively high, but the migration speed of the hydrocolloid is low because it is hydrated water.
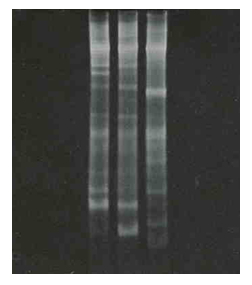
写真Ⅰ-3 DNA断片の電気泳動分析-活性汚泥・細菌群の16S-rDNA解析事例
Photo I-3 Electrophoretic analysis of DNA fragments-Example of 16S-rDNA analysis of bacteria of an activated sludge.
References
1) 池上 徹(栗田工業KCRセンター):水処理教室-凝集処理、https://kcr.kurita.co.jp/wtschool/012.html
2) 化学工学協会編:化学工学便覧、丸善、1978
3) 北原 文雄・渡辺 晶:界面電気現象-基礎・測定・応用-、共立出版、1972
4) 北原 文雄:界面・コロイド化学の基礎、講談社、1994
5) 作花 済夫:ゾル-ゲル法の科学、アグネ承風社、1988
6) 小林 幹雄・他4名共編:数学公式集:共立出版、2005
7) 長谷川 裕也:コロイド化学、http://sekatsu-kagaku.sub.jp/colloid.htm
8) 福田 清成・中垣 正幸:コロイド化学の基礎、大日本図書、1969
9) 古澤 邦夫:ぶんせき、5、247-254(2004)
10) 粉体工学会編:液相中の粒子分散・凝集と分離操作、日刊工業新聞社、2010
11) 松村 淳司:界面・電気化学講義、http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf
12) 用水廃水便覧編集委員会編:用水・廃水便覧、丸善、1973
13) Alonso, M. and E. J. Finn, E.J.: University Physics-Volume Ⅱ Field and Waves, Addison-Wesley Publoshing Co., 1967
14) Bergdtrom, L.: Hamaker Constants of Inorganic Materials, Advances in Colloid and Interface Science, 70, pp.125-169, 1997
15) Derjaguin, B.V.: Kolloid Z. (in German). Vol.69, No.2, pp.155–164, 1934
16) Hamaker, H.C.: Physica IV, No.10, 1058, 1937
17) Otterwill, RH & A. Watanabe: Kolloid. Z., Vol.170, p.133, Fig.1, p.135, Fig.4( 1960)
References
1) Ikegami Tohru (Kurita KCR Center): Water Treatment Class-Agglomeration, https://kcr.kurita.co.jp/wtschool/012.html
2) The Society of Chemical Engineers, Japan Ed.: Chemical Engineering Handbook, Maruzen, 1978
3) Kitahara Fumio & Akira Watanabe: Interface Electrical Phenomena-Basics, Measurements and Applications-, Kyoritsu Shuppan, 1972
4) Kitahara Fumio: Fundamentals of Interface and Colloid Chemistry, Kodansha, 1994
5) Sakka Sumio: Science of Sol-Gel Method, Agne Jofusha, 1988
6) Kobayashi Mikio and 4 others co-edited: Mathematical formula collection: Kyoritsu Shuppan, 2005
7) Hasegawa Yuya: Colloid Chemistry, http://sekatsu-kagaku.sub.jp/colloid.htm
8) Fukuda Kiyonari and Masayuki Nakagaki: Fundamentals of Colloid Chemistry, Dainippon Books, 1969
9) Furusawa Kunio: Bunseki, 5, 247-254 (2004)
10) The Society of Powder Technology, Japan, Ed.: Dispersion/Agglomeration and Separation of Particles in Liquid Phase, Nikkan Kogyo Shimbun, 2010
11) Matsumura Atsushi: Interfacial/Electrochemical Lecture, http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf
12) Editing Committee for Water/waste water handbook: Manual for Water and Waste Water Manual, Maruzen, 1973
(The following is the same as the description in the left column.)
掲載日:2019年03月29日
更新日:2019年04月21日
更新日:2020年07月14日(英語版を追加)
Pubulished: March 29, 2019.
Updated: April 21, 2019.
Updated: July 14, 2020 (English version added).
