村上定瞭(水浄化フォーラム)
Ⅰ.コロイドと界面現象
1.コロイドとは
2.疎水・親水コロイド
3.疎水コロイドの分散と凝集
4.親水コロイドの塩析
5.会合コロイドとミセル
6.コロイド溶液の物性
Ⅱ.解説
解説(A) 粒子界面の静電気現象
解説(B) 疎水性2粒子系の相互作用
解説(C) 粒子界面電荷の発生
解説(D) 電解質効果とSchulze-Hardy法則
解説(E) 凝集速度
解説(F) 表面張力と界面活性
解説(G) 界面活性剤の特性
解説(H) 吸着エネルギーと平衡式
解説(J) 高分子吸着と分散・凝集
付録 疎水コロイド相互作用の計算ソフト
(ダウンロード)
参考文献
関連ページ
分散・懸濁粒子の凝集分離
Ⅱ.解 説
解説(H) 吸着エネルギーと平衡式
活性炭・シリカゲルのように、固体の表面だけでなく内部にまで細孔を有する多孔質では、孔の大きさが分子のオーダーに近づくと、固相の表面だけでなく吸着質が内部孔へ侵入できるので、吸着と吸収との区別がつかなくなる。こうした多孔質への吸着現象を収着と呼ぶ場合がある。
固体表面への吸着では、分子またはイオンと固体表面との相互作用が問題になる。固体表面には一種の力の場があり、この点で気相・液相界面の吸着と趣を異にしている。吸着現象にも平衡と速度の2つの視点があるが、ここでは吸着平衡の面から扱っていく。
1.物理吸着と化学吸着
物理吸着では、吸着の際に発生する吸着熱は気体の凝縮熱に相当するもので、そのエネルギーは低い。他方、化学吸着では、吸着熱は高く数十kJ以上になる。物理吸着は、温度を上げたり希釈したりすると、脱着が可逆的に起こるのに対し、化学吸着したものは脱着が容易に起こらず不可逆性が強い。化学吸着は一種の化学反応であるから、吸着に際して活性化エネルギーを必要とし、吸着速度は遅くなる。表H.1 に物理吸着と化学吸着との特性の比較を示した。
化学吸着は水素や酸素の金属表面への吸着で見られる。このとき、金属表面で分子から原子への解離が起きることがある。解離吸着した原子は反応しやすい状態となっている。エチレンの水素化において、ニッケルなどの金属が触媒となるのはこのためである。高級脂肪酸が有機溶液から金属表面に吸着するとき、表面に金属セッケンを作って強く吸着する。これは化学吸着である。高級脂肪酸が潤滑作用をするとき、境界潤滑といわれる領域では、化学吸着した高級脂肪酸の単分子層が働いているといわれる。

2.吸着の実験
2.1 吸着量の測定
(A)気体吸着
一定圧 pでの吸着後の体積減少量をΔv、温度をT [K]、吸着媒の質量を w [g]とすると、気相を理想気体と仮定して、吸着量 Aは次式で表される.
A = pΔv/(RTw) [mol/g] (H.1)
吸着媒の比表面積が既知のとき、Aはmol/m2の単位で得られる。気体吸着では、吸着による吸着媒の重量増加を直接に、測定試料を載せた石英バネ秤の伸びから求める方法もある。
(B)溶液吸着
これは溶質の濃度を測定することに帰着する。溶質が光を吸収する場合は紫外可視分光光度計で精度よく濃度が求められる。赤外分光光度計も用いられるが、精度が低い。溶媒・溶質に屈折率差がある場合には、屈折率または屈折率差の測定も用いられる。一般的方法として、溶媒を蒸発させて残った溶質の質量を測る重量法があるが、溶質が吸湿性とか、易分解性であったりすると精度がよくない。
2.2 吸着状態
2.3 吸着等温線
吸着等温線の形は気体吸着と溶液吸着とではいくぶん異なる。よく見られる吸着等温線の形を図H.1 に示した。(a) はLanguir型といわれ、気体吸着、溶液吸着両者で見られる。(b)はBET型といわれ、気体吸着で見られる。poは吸着質の飽和蒸気圧である。(c)はFreundlich型といわれ、溶液吸着で見られる。
(d)は階段型ともいうべきもので、界面活性剤水溶液の吸着で見られる。例えば、第一の平坦部分は単分子層の被膜形成、第二の平坦部分は単分子層の上に第二の分子層の被膜形成に対応している。これは2分子膜の形成で、生体の細胞膜のモデルで人工的に作成でき、ベクシルと呼ばれる。
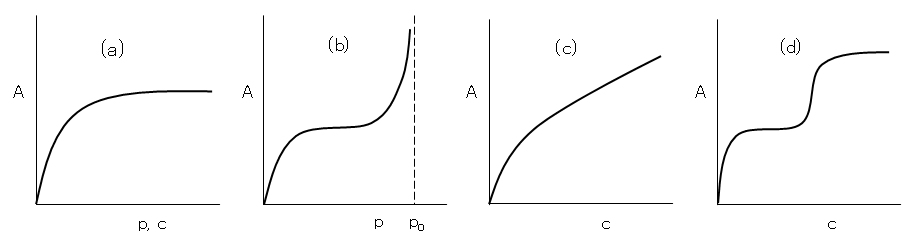
図H.1 吸着等温線の4つ型
(a) Langmuir 型、(b) BET 型、(c) Freundlich 型、(d) 階段型
3.吸着の理論
3.1 吸着の熱力学
吸着は、吸着質の分子またはイオンと吸着媒の固体表面との相互作用であることはすでに触れた。吸着は、広義の化学反応とみることができ、吸着は吸着質と吸着媒との結合に、脱着は結合が切れることに相当する。吸着質分子(またはイオン)を捕捉する固体表面の場所を吸着サイトといい、次の式が成り立つ。
吸着質分子 + 吸着サイト ⇄ 吸着質分子・吸着サイト
このときの質量作用則は、
ams/(am・as) = K’ (H.2)
a:活量;添字m、s、ms:分子、サイト、分子・サイト(吸着状態);K’:平衡定数
asは吸着の影響を受けないので一定、気体吸着ではam ∝ p(平衡圧)、ams(吸着量)であるから、新たな平衡定数Kは次式で示される。
A/P = K (H.3)
K:新たな平衡定数
平衡定数の温度変化に関するvan’t Hoff の式
ln K1/K2 = – ΔH/R・(1/T1 – 1/T2) (H.4)
を適用するために、図H.2のように、2つの温度T1、T2における吸着等温線を考える。この図に示すある吸着量Aoについて、式(H.3)を適用すると、次式が成り立つ。
Ao/p1 = K1 Ao/p2 = K2
上式の関係から、次式が得られる。
K1/K2 = p2/p1 (H.5)
式(H.4)において、反応熱ΔH→吸着熱ΔHa(ΔHa:熱力学的に吸熱を正とする)とおいて、式(H.5)の関係から、次式の関係が得られる。
ln p1/p2 = – ΔHa/R・(1/T1 – 1/T2) (H.6)
一般に、吸着量は温度が上がると減少するので、図H.2においてT1>T2である。また、同図からp1>p2であるので、式(H.6)からΔHa<0 となる。すなわち、吸着熱は一般に発熱反応である。この結論は Le Chatelierの原理からも導かれる。さらに、式(H.6)より吸着熱を定量的に求めることができる。
吸着熱が発熱ということは次の考察からもわかる。吸着過程について、熱力学の基本式
ΔG = ΔH – TΔS (H.7)
を考える。「吸着が起きる」ということはΔG<0である。配置エントロピーを考えると、吸着に伴い吸着質分子の運動の自由度が減少するので、ΔS<0 となる。このことから、式(H.7)が成立するためにはΔH<0であることが分かる。
吸着質分子 + 吸着サイト ⇄ 吸着質分子・吸着サイト
このときの質量作用則は、
ams/(am・as) = K’ (H.2)
a:活量;添字m、s、ms:分子、サイト、分子・サイト(吸着状態);K’:平衡定数
asは吸着の影響を受けないので一定、気体吸着ではam ∝ p(平衡圧)、ams(吸着量)であるから、新たな平衡定数Kは次式で示される。
A/P = K (H.3)
K:新たな平衡定数
平衡定数の温度変化に関するvan’t Hoff の式
ln K1/K2 = – ΔH/R・(1/T1 – 1/T2) (H.4)
を適用するために、図H.2のように、2つの温度T1、T2における吸着等温線を考える。この図に示すある吸着量Aoについて、式(H.3)を適用すると、次式が成り立つ。
Ao/p1 = K1 Ao/p2 = K2
上式の関係から、次式が得られる。
K1/K2 = p2/p1 (H.5)
式(H.4)において、反応熱ΔH→吸着熱ΔHa(ΔHa:熱力学的に吸熱を正とする)とおいて、式(H.5)の関係から、次式の関係が得られる。
ln p1/p2 = – ΔHa/R・(1/T1 – 1/T2) (H.6)
一般に、吸着量は温度が上がると減少するので、図H.2においてT1>T2である。また、同図からp1>p2であるので、式(H.6)からΔHa<0 となる。すなわち、吸着熱は一般に発熱反応である。この結論は Le Chatelierの原理からも導かれる。さらに、式(H.6)より吸着熱を定量的に求めることができる。
吸着熱が発熱ということは次の考察からもわかる。吸着過程について、熱力学の基本式
ΔG = ΔH – TΔS (H.7)
を考える。「吸着が起きる」ということはΔG<0である。配置エントロピーを考えると、吸着に伴い吸着質分子の運動の自由度が減少するので、ΔS<0 となる。このことから、式(H.7)が成立するためにはΔH<0であることが分かる。
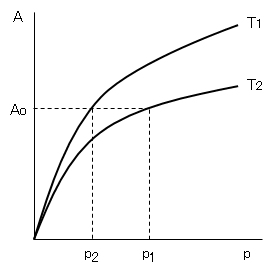
図H.2 2つの吸着等温線から吸着熱を求める操作
3.2 吸着等温式
図H.1の意味と吸着等温式において、(a)のLangmuir式および(c)のFreundlichについて説明する。Langmuir式は、水浄化における分散・凝集に関係の深い界面活性剤や高分子電解質の吸着特性をよく説明できる。また、Freundlichは実験式であって、定数の物理的意味は明確でない。しかし、高分子電解質の吸着において、濃度依存性を示すパラメータ1/n(または、α)と立体的吸着形態との間に、一定の傾向が観察される。本ページでは、(b)・(d)についての説明は、省略するので、興味ある方は、ページボトムに記載の文献 [北原, 1994]を参考にされたい。
(A) Langmuirの吸着等温式
気体吸着では、吸着量をA、平衡圧をpとするとき、この式は、
A = aAmp/(1 + ap) (H.8)
と表される。ここで、a、Amは定数である。A は0℃、101.3 kPa(1気圧)に換算した気体の体積値も用いられる。溶液吸着ではpの代わりに平衡濃度cを用いる。p が大きいときは 1 + ap ≒ ap だから、A = Am、すなわち、Amは飽和吸着量である。Langmuirの式は単分子層吸着であり、下記に示す動的平衡の考えから誘導できる。Langmuirは吸着の過程を次のように化学的に考えた。
(1) 固体表面には吸着のサイトが存在している。
(2) サイトには1分子しか吸着できない(単分子層吸着の考え)。
(3) 吸着平衡においては,吸着速度と脱着速度が等しい(動的平衡の考え)。
吸着平衡における吸着速度v+、脱着速度v–は次のようになる。
v+ = k+p(1 – θ) (H.9)
v– = k–θ (H.10)
ここで、p は気体の平衡圧、θ は吸着しているサイトの割合、k+、k–はそれぞれの速度定数である。平衡状態では、
v+ = v– (H.11)
であるから、
θ = (k+/k–)p/[1 + (k+/k–)p]] (H.12)
平衡圧pのときの吸着量をA、飽和吸着量をAmとすると、θの定義から
θ = A/Am (H.13)
である。k+/k– = aとおくと、式(H.12)、式(H.13)から式(H.8)が得られる。
速度定数に関するArrheniusの式
k = B exp[-E/(RT)] (H.14)
B:頻度因子、E:活性化エネルギー
この式を用いると、
a = k+/k– = (B+/B–)exp[-(E+ – E–)/(RT)] = (B+/B–)exp[-ΔHa/(RT)] (H.15)
ここで、E+ – E– = ΔHa(吸着熱)の関係を使った(図H.3、参照)。すなわち、a は吸着熱に対応する量である。Langmuirの式には質(吸着の強さ-吸着熱)と量(飽和吸着量)に関する定数が入っている。
Langmuirの式(H.8)を変形すると、
p/A = 1/(aAm) + p/Am (H.16)
図H.4に示す p/A-pの直線関係の成立からLangmuirの式の適用が確かめられ、その勾配と縦軸の切片から定数 a、Amが求められる。この図をLangmuir プロットともいう。
(B) Freundlichの吸着等温式
吸着量A、平衡濃度 c とすると、Freundlichの吸着式は
A = kc1/n (H.17)
k、n:定数
と表される。この式は実験式であって、定数の物理的意味ははっきりしない。吸着媒が活性炭、シリカゲルのように多孔質の場合にあてはまる。これら吸着媒は表面構造が複雑で、多種のサイトがあると考えられる。それぞれのサイトについて、異なるLangmuirの式が成立し、それらの和が式(H.17)になると解釈できる。この式は実験データを整理するのに便利である。
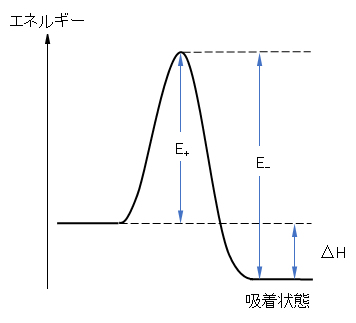
図H.3 吸着速度過程におけるエネルギー関係
E+:吸着の活性化エネルギー、E–:脱着の活性化エネルギー、Ha:吸着熱
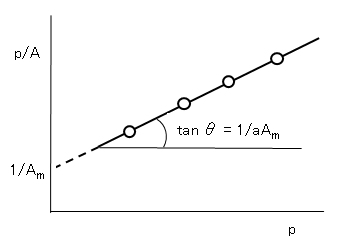
図H.4 Langmuirの吸着式のパラメータ(a、Am)の決定
4.溶液の吸着
溶質をよく溶かす溶媒は溶質の吸着を阻害し、吸着媒に親和性のある溶媒は溶質の吸着を阻害する。図H.5に例を示す。図の3本の吸着等温線は3つの脂肪酸同族体の吸着を定性的に示したものである。溶質の親水性が酢酸 CH3COOH>プロピオン酸 C2H5COOH>酪酸 C3H7COOHであることを考えると、親水、疎水の親和性から曲線の上下の順序は理解できる。
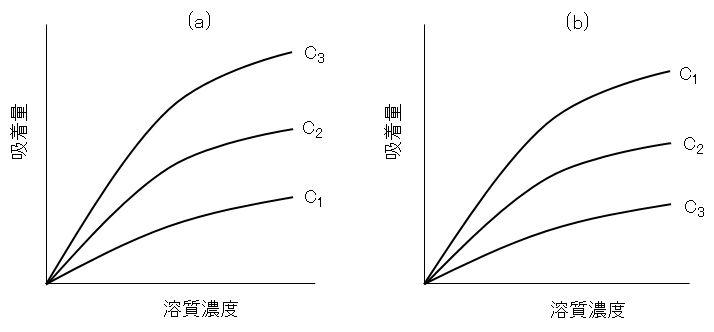
図H.5 吸着等温線への溶媒効果(相対量での比較)
(a) 水-活性炭系、(b) トルエン-シリカゲル系
C1:酢酸、C2:プロピオン酸、C3:酪酸
5.高分子の吸着
(1) 吸着速度が遅い。低分子では、掻き混ぜていると1~2 時間以内には吸着平衡に達するが、高分子では数時間以上を要し、1 昼夜かかることもある。
(2) 吸着形態がいくつか存在する。図H.6に代表的な3つの例をあげた。
(3) 不可逆吸着を示す場合が多い。図H.6の(a) 水平型、(c) ループ型の場合がそうである。
(4) 吸着等温線はおおむねLangmuir型である。これは分子が大きいため、吸着媒からの力の場が2 分子以上には及ばないためである。
吸着形態が図H.6の3つの型のいずれになるかを実験的に決めるには次式による。
Am = KMα (H.18)
Am:飽和吸着量;M:分子量; K、α:定数
高分子を分子量分別してMの異なる試料を調製し、吸着実験によりAmを求め、log Amとlog Mとのプロットよりαを決める。α = 0 ならば水平型、α = 1 ならば垂直型、0<α<1ならばループ型である。
ポリ酢酸ビニルのベンゼン溶液からガラス球への吸着では、分子量105~106の範囲でα = 0 である(水平型吸着)。エチレン・酢酸ビニル共重合体のベンゼン溶液からガラス球への吸着では、分子量11万~31万の範囲でα = 1/3 である(ループ吸着) [Mizuhara et al., 1969, 1970]。
高分子吸着の溶媒依存性は、良溶媒ほど吸着量が減少する。これは上記の4.溶液の吸着で述べたことと同様である。高分子の粒子系への作用にについたは、次の解説(J)で詳しく解説する。
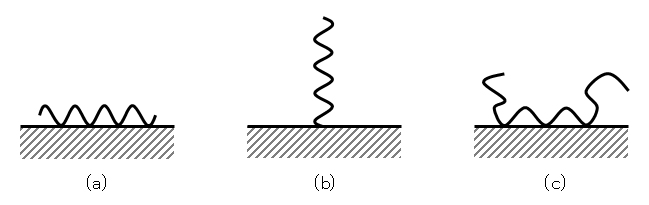
図H.6 高分子の3つの吸着形態
(a) 水平型(train)、(b) 垂直型(tail)、(c) ループ型(loop)
目次へ
解説(J) 高分子吸着と分散・凝集
高分子が非電解質ならば非電気的な層を作り、高分子電解質ならば電荷を帯びた層を作る。ここでは簡単のため、高分子非電解質を扱う。非イオン界面活性剤が吸着した場合も、効果は比較的小さいが同様に論じられる。
1.高分子吸着層の特性
ループ型吸着の場合、図 J.1のようなスキームが描かれ、それぞれの部に、トレイン(train)、ループ(loop)、テール(tail)の名が付けられている。吸着層の厚さδという量がしばしば用いられる。テールの長さは揺らいでいて一定ではないが、統計的な値または測定される値としてのδである。厚さを求める方法はいくつかあるが、現在信頼できる測定法は、動的光散乱法で粒子半径Rを求め、裸の粒子の半径 aとの差δ = R – a とする方法である。
吸着の被覆率という表現が使われる。吸着高分子が粒子表面をどの程度被覆しているかという意味で、吸着層の疎密を表している。定量的には Langmuir型の吸着等温線 [図H.1 (a)]が飽和値に達したところが被覆率 ’1’で完全被覆、それ以下の吸着量のところは飽和値との比で被覆率が表される。
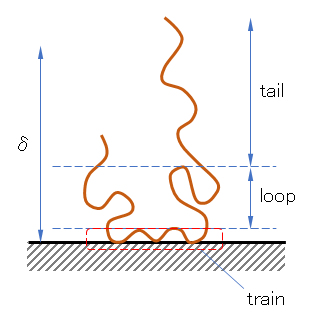
図 J.1 粒子表面への吸着高分子のモデル図
2.吸着層の分散・凝集作用
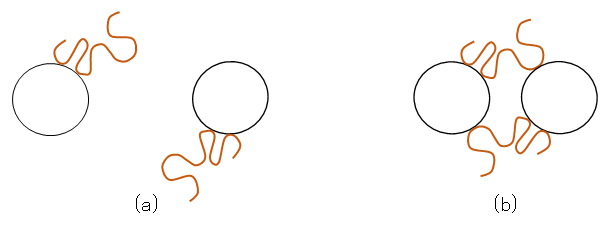
図 J.2 粗な吸着高分子による粒子間の橋かけ凝集のモデル図
(a):粒子表面への粗な高分子吸着、(b):吸着高分子の橋かけによる粒子の凝集
以上述べてきた高分子濃度による凝集作用と分散作用を安定度比との関係から図示すると図 J.4のようになる。高分子は濃度co以下では凝集剤、co以上では分散剤として慟くことになる。高分子量で、良溶媒ほどco以下では効果的な凝集剤であり、co以上ではよい分散剤となる。水処理剤として汚濁水中の微細な分散物質を凝集させるのに使用される高分子凝集剤にはポリアミドの分子量数百万に及ぶものがある。
凝集分散作用をする高分子の例として、ポリスチレンラテックスに対するポリエチレンオキサイド(PEO)があげられる。PEOの分子量が900万と大きいものでは、濃度とともに図 J.4に示されるような典型的な凝集→分散の作用が観察されている。曲線の極小(凝集効果最大)の濃度c1は0.9mg/L、転換点coは1.4 mg/Lであることが測定された。低分子量6万のPEOでは吸着層の厚さが小さいためか分散作用はほとんど見られなかった [Ash & Clayfield, 1976]。
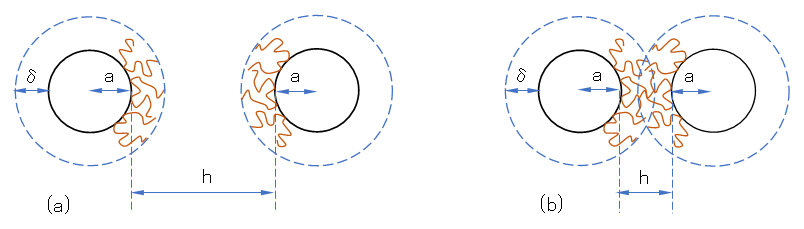
図 J.3 密な高分子吸着層による反発作用のモデル図
(a):粒子を覆う密な高分子吸着層、(b):粒子接近での高分子吸着層の重なりによる反発作用
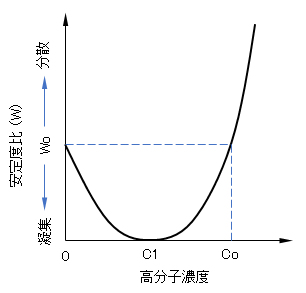
図 J.4 高分子濃度と凝集・分散作用の関係
W:安定度比、Wo:高分子濃度 ’0’におけるW、
W<Wo:凝集、W>Wo:分散
V = VR + VA (J.1)
となるが、これを図 J.5に示した。図に見られるように、VAは遠くまで及ぶので、必ずVminの負の谷が生じる。しかし、Vmin ~ kTならば粒子は十分に分散している。2δが小さいときは、Vminの谷が深くなってしまう。Vminを浅くして分散作用をする条件は、厚くて密な吸着層の形成である。これには吸着高分子の分子量を大にすること、吸着量を大きくすること、高分子が溶媒中でよく拡がること(良溶媒を選ぶこと)が条件となる。
<説 明>
VRは次のように解析的な式で表されている[Ottewill, 1968]。δ>h/2のとき、
VR = 4πkTca2/(3v1・ρ22)・(φ1 – κ1)(δ – 2/h)2(3a + 2δ + h/2) (J.2)
ただし、δ/2のときは相互作用が起きないので、VR = 0 。
ここで,caは吸着層内の高分子濃度(吸着量とδから計算できる)、v1は溶媒の分子体積、ρ2は高分子の密度、φ1 – κ1は高分子と溶媒の相互作用を表すパラメータ(粘度から求められる)、h は2粒子の最短表面間距離、a は粒子半径である。
良溶媒系ではφ1 – g1>0であるから、VR>0となり、反発作用が起きる。
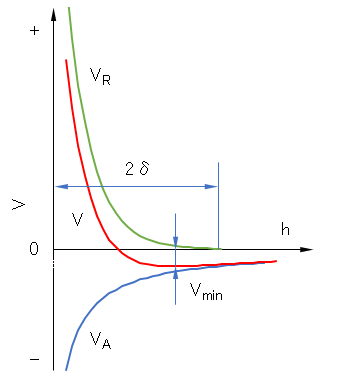
図 J.5 吸着層を有する2粒子系のポテンシャルエネルギー曲線を示す一例
3.枯渇効果
吸着性高分子の場合、濃度増加により密な吸着層を作り、粒子に対して分散作用をすることは前節で述べた。さらに高分子濃度を増加させるとどうなるか。吸着が飽和に達し、もはや吸着できなくなった高分子は、ちょうど非吸着性高分子と同様な挙動をして枯渇凝集が起きる。さらに高分子濃度を高くすると、枯渇領域が生じにくくなって枯渇凝集しにくくなり、再分散するようになる。
枯渇凝集は高分子の拡がりが関係するので、枯渇凝集の始まる高分子濃度は高分子の分子量、高分子と溶媒との相互作用(溶解性)に依存する。また、粒子濃度が大きいと低い高分子濃度で枯渇凝集が起きる。
実験的には、分散系の粘度測定から枯渇凝集の生起や再分散の発生を知ることができる。たとえば、15%のポリスチレンラテックスに対し、吸着性のヒドロキシプロピルセルロース(分子量90万)の0.4%で、枯渇凝集による粘度の急増がみられたいる。この粘度変化はずり速度1 s-1の弱いずり力の場合に観測されたのに対し、100 s-1の大きいずり速度では観測できなかった[Nashima & Furusawa, 1988]。
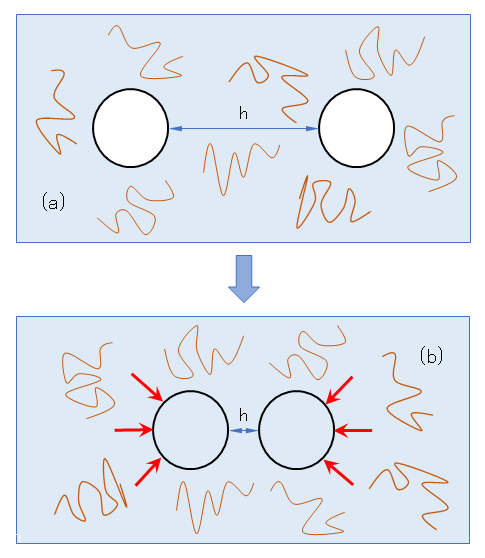
図 J.6 枯渇凝集の原理を示す模式図
4.吸着層と電気二重層の共存効果
橋かけ凝集が起きるためには、吸着が疎であって、図 J.7(a)に示すように吸着高分子の拡がりδが粒子間距離 hを越える必要がある(δ>h)。しかし、電気二重層の拡がりの2倍(2/κ)がδを越すと(2/κ>δ)、橋かけができなくなる[図 J.7(b)]。δ(二重層の厚さ)は拡散的で一定値ではないので、上記の条件は定性的なものではあるが、次のことが言える。塩濃度を減らすと二重層が拡がって高分子の橋かけ凝集は起きにくくなる。
上記の結論は実験的に確かめられている。たとえば KCl 10 mol/L水溶液中で、ポリビニルアルコールを飽和吸着させたAgI コロイドに、裸の(未吸着の)AgI コロイドを加えると凝集が起きることが観測された。これは橋かけ凝集である。しかしKCl濃度を2 mol/Lと低くした溶液中で同じ実験をしたところ凝集は起きなかった。これは二重層が拡がり、図 J.7(b)に示す状況が生じたためである[Fleer & Lyklema, 1974, 1976]。
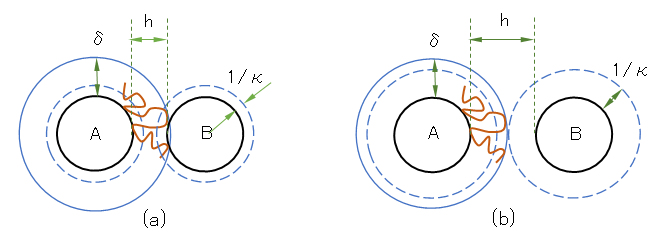
図 J.7 電気二重層と吸着層の共存効果のモデル図
(a):橋かけ凝集が起こる(δ>2/κ、δ>h)、(b):橋かけ凝集が起こらない(δ<2/κ)
目次へ
参考文献
Alonso, M. and E. J. Finn, E.J.: University Physics-Volume Ⅱ Field and Waves, Addison-Wesley Publoshing Co., 1967
Ash, S. G., K. I. Clayfield: J. Colloid Interface Sci., 55, 645(1976)
Bergdtrom, L.: Hamaker Constants of Inorganic Materials, Advances in Colloid and Interface Science, 70, pp.125-169, 1997
Derjaguin, B.V.: Kolloid Z. (in German). Vol.69, No.2, pp.155–164, 1934
Dynstee, E. F., E. Grunwald: J.Am. Chem. Soc., 81, 4540(1959
Eischens, R. P., S. F. Francis, W. A. Pliskin: J. Phys. Chem., 60, 196(1956)
Fleer, G. J., J. Lyklema: J. Colloid Interface Sci., 46, 1(1974); ibid., 55, 228(1976)
Fowkes, F. M.: Ond. Eng. Che., 56, 41(1964)
Gobe, M., K. Kon-no, K. Kandori, A. Kitahara: J. Colloid Interface Sci., 93, 293(1983)
Hamaker, H.C.: Physica Ⅳ, No.10, 1058(1937)
Hoffman, H., G. Ebert: Angew Chem. Int. Ed., 27, 902(1988)
Imae, T, R. Kamiyama, S.Ishida: J. Colloid Interface Sci., 108, 215(1985); J. Phy. Chem., 90, 5216(1986); Colloid Polymer Sci., 265, 1090(1987)
Israelachvili, J. N., D. J. Mitchell, B. W. Ninham: J. Chem. Soc. Faraday Trans.Ⅱ, 72, 1525(1976); Biochem. Biophs. Acta, 470, 185(1977)
Mizuhara, K., K. Hara, T. Imoto: Kolloid-Z. u. Z. Polymere, 229,17(1969); ibid., 237,279(1970)
Nashima, T., K. Furusawa: Chem. Lett., 1253(1988)
Ogino, K., M. Nakamae, M. Abe: J. Phys. Chem., 93, 3704(1989)
Otterwill, R. H. & A. Watanabe: Kolloid. Z., Vol.170, p.133, Fig.1, p.135, Fig.4(1960)
Otterwill, R. H., T. Walker: Kolloid-Z. u. Z. Polymere, 227, 108(1968)
Shikata, T., Y. Sakaguchi, H. Uragami, A. Tamura, H. Hirata: J. Colloid Interface Sci., 119, 291(1989)
池上 徹(栗田工業KCRセンター):水処理教室-凝集処理、https://kcr.kurita.co.jp/wtschool/012.html
化学工学協会編:化学工学便覧、丸善、1978
北原 文雄・渡辺 晶:界面電気現象-基礎・測定・応用-、共立出版、1972
北原 文雄:界面・コロイド化学の基礎、講談社、1994
作花 済夫:ゾル-ゲル法の科学、アグネ承風社、1988
小林 幹雄・他4名共編:数学公式集:共立出版、2005
長谷川 裕也:コロイド化学、http://sekatsu-kagaku.sub.jp/colloid.htm
福田 清成・中垣 正幸:コロイド化学の基礎、大日本図書、1969
粉体工学会編:液相中の粒子分散・凝集と分離操作、日刊工業新聞社、2010
松村 淳司:界面・電気化学講義、http://res.tagen.tohoku.ac.jp/~liquid/MURA/kogi/kaimen/kaimen2002/2002-6.pdf
用水廃水便覧編集委員会編:用水・廃水便覧、丸善、1973
目次へ
掲載日:2019年03月29日
更新日:2019日05月01日
