村上定瞭(水浄化フォーラム)
1.電極電位の制御と電極・溶液界面での電子移動
(1)電界電子放出
(a) 電子放出
常温における気相中での電界放出では電極間に数十kVの極めて強い加電圧が必要となるが、液相での電気分解では数V程度の加電圧で電極表面で電子移動(放出・受入)が起こる。本節では、電気分解の理解を深めるため、電気分解との相違を説明する。
(b) 電界放出と電気分解
電界放出の応用では、金属表面から放出された電子を電界で加速し、ガス分子・原子に衝突させて発光(蛍光灯やオゾン発生、気体化した物質の分析)やイオン化(質量分析)をしたり、進行方向を電場・磁場で制御して電子を正確にターゲットに当てて発光(TVブラウン管)や回折・散乱による材料の表面分析を行う。
電気分解の応用では溶液中の物質に対して、電子の授受による酸化還元反応を行い、目的物質の析出・分解、あるいは、その電圧あるいは電流から目的物質の定性・定量分析などを行う。また、材料の表面特性や腐食・防食機序を解明する上でも,電気化学は重要な役割を担う。
(c) 電界放出のメカニズム
図1(A)に、真空に近い容器内に先端が鋭利な電極(作用電極)と対極(広い表面積)を設置し、高圧の直流電源(作用極を正極、対極を負極)に接続し、電界を加えたときの作用極近傍の状況をイメージ化したものである。
作用電極から距離xにある電子のポテンシャルエネルギーを示す。φim(x) は、導体平面に対する鏡像電荷よる電位を示す。φex(x) は、両極に印加した外部電界による電位である。このことから、外部電界が加えられたときの、作用電極近傍での電位は、φ(x) = φim(x) + φex(x) となり、作用極から電子を放出するためのエネルギー障壁 φo は φb に減少する。また、印加電圧が大きくなるほど、φex(x) の傾きが大きくなり、φ(x) の極大値における x 値(電極表面からの距離)は小さくなる。今、フェルミ準位 Efとφ(x)の2交点の距離を L とすると、トンネル効果は、エネルギー障壁の高さφbが低いほど、厚さ L が薄いほど、その起こる確率が高くなる。常温では、φex(x) が 109 V/m 近くなるとトンネル効果が顕著となるといわれる。これは電極表面~10Åの間に1Vの電圧を印加した電界の強さに相当する。
(d) 電界イオン顕微鏡
ところで、上記の現象は電極が自由空間へ電界電子を放出する例であるが、電極が気相中原子から電子を受け取る例を上げる。図1(B)・(C)は、低圧のヘリウム原子Heを封入し、作用電極を正極、対極を負極としたときの、He原子が作用極に衝突した場合のイメージ図である。φA(x)は、He原子と外部電界による合計ポテンシャルを示す。図(C)に示すように作用極近傍のφex(x)は高く、エネルギー障壁が高いので、He原子が何度も作用極(+)に衝突するうちにトンネル効果により、Heの電子が作用極に転移する。生じた He+ は電界により加速されて対極へ衝突し、図(B)のイメージで対極より電子を受け取り、He原子へ戻る。対極(スクリーン)に蛍光物質を塗布すると高速のHe+の衝突により蛍光を発する。この蛍光を観察することにより、対極表面の原子配置に関する情報が得られる。この原理を応用したものが、電界イオン顕微鏡である。
電気分解の応用では溶液中の物質に対して、電子の授受による酸化還元反応を行い、目的物質の析出・分解、あるいは、その電圧あるいは電流から目的物質の定性・定量分析などを行う。また、材料の表面特性や腐食・防食機序を解明する上でも,電気化学は重要な役割を担う。
作用電極から距離xにある電子のポテンシャルエネルギーを示す。φim(x) は、導体平面に対する鏡像電荷よる電位を示す。φex(x) は、両極に印加した外部電界による電位である。このことから、外部電界が加えられたときの、作用電極近傍での電位は、φ(x) = φim(x) + φex(x) となり、作用極から電子を放出するためのエネルギー障壁 φo は φb に減少する。また、印加電圧が大きくなるほど、φex(x) の傾きが大きくなり、φ(x) の極大値における x 値(電極表面からの距離)は小さくなる。今、フェルミ準位 Efとφ(x)の2交点の距離を L とすると、トンネル効果は、エネルギー障壁の高さφbが低いほど、厚さ L が薄いほど、その起こる確率が高くなる。常温では、φex(x) が 109 V/m 近くなるとトンネル効果が顕著となるといわれる。これは電極表面~10Åの間に1Vの電圧を印加した電界の強さに相当する。
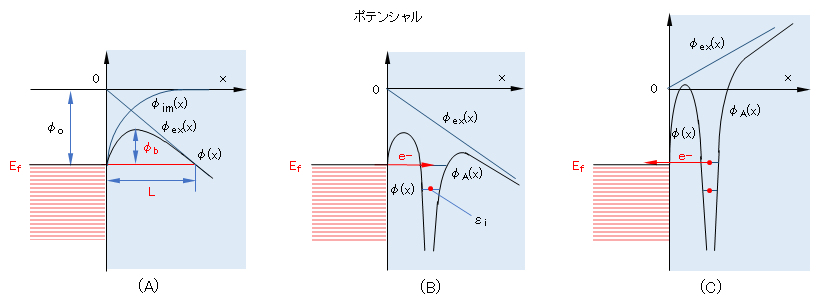
図1 外部電界下での金属電極表面近傍のポテンシャルとトンネル効果による電子移動
Ef-フェルミ準位、x-電極表面からの距離、φo-仕事関数、φb-電界電子放出のエネルギー障壁、L-エネルギー障壁の厚さ、φim(x)-鏡像電界による電位、φex(x)-外部電界による電位、φ(x)-φimとφexの合計電位、φA(x)-原子Aと外部電界による電位の合計ポテンシャル、εi-価電子のエネルギー準位
(2)電極-溶液界面での電子移動
(a) 物質間の電子移動の要件
要件① 両物質に拘束された電子が、そのエネルギー障壁(厚さL)を越えて,移動できる距離に、すなわち、トンネル効果が起こる程度に、接近すること。
要件② W電子とX電子の波動関数のエネルギー準位が一致すること。
要件③ 電子の移動時間Δtにおいて、ψX(r)が変化しないこと。
以上のことについて、少し詳しく説明する。
要件①
これは、波動関数ψW(r)とψX(r)が重なる距離にまで接近することを意味し、そのときのトンネル効果の起こる確率 P は exp (-2πL/λ) に比例する。エネルギー1eVの電子の物質波λは25Åであるので、L = 5、10、15Åとすると、P ∝ 0.28、0.08.2、0.023となり、電極表面に対して分子 X が 10Å程度接近すれば十分電子移動が可能であることが示される。
要件②
トンネル効果では、エネルギー障壁を越えた電子の物質波の波長は変化しないことによる(確率分布|ψ(r)|2は減少するが,その固有エネルギー E は変化しない。)。電子を供与する側の占有軌道エネルギー準位と受け取る側の空軌道のエネルギー準位が一致すること(EW = EX)である。
要件③
作用電極は溶液中に位置を固定されているが、液相中の物質Xは常に動いている。トンネル効果が完了するまで、分子XはLの位置に保持されていることが前提となる。ところで、溶液中のX分子は溶媒により囲まれており、気相中よりはるかに小さいと思われるが、計算が複雑になるので気体粒子として扱う。気体粒子の運動論によると、電子の速度√<ve2>と分子Xの速度√<vX2> の相対比は、それらの質量から、√(mX/me)で示される。X/X+系を[Fe(CN)6]4-/[Fe(CN)6]3-系とすると、√(mX/me) = 622 となる。また、X → X + e– に分裂するとき、運動量保存の法則から、ve/vX = 3.86 x 105となる。
いずれにしても、X/X+がトンネル効果が起こる L の範囲内に接近したとき、電子移動が完了するまでに、時間的に X/X+分子はその位置に十分留まっている。
以上のことを踏まえた上で、次項の説明を行う。
(b) 電極界面での電子移動
<活性物質 X/X+の電荷による電極表面への接近の差異>
気相中では、電界は平行電極間の空間において均一であるので、図1(B)(C)に見られるように、作用電極の電位が正極(+)または負極(-)の違いによって、電荷を有する活性物質は、その正負によって、引力または斥力が働く。しかし、図4(A)に示すように電解セル内では支持電解質が多量に存在するので、電界は電極の電気二重層に集中し、これ以外の領域での電界は極めて弱く、荷電物質も空間的方向に関係なく自由に動く。ただし、支持電解質の濃度が低く、電位勾配(セル電流が流れるとき)がある場合には、荷電粒子はこの電界により特定方向へ移動する(電気泳動)が、ここでは支持電解質は十分で溶液内の電界は生じないこととする。以上のことから、活性物質X/X+は、作用電極の電位によらず、その電気二重層の界面まで、その電荷による影響を受けることなく接近することができる。
支持電解質溶液と電場
電気の導体(金属、半導体、固体電解質、電解質溶液など)に電圧 Eを加えると、導電媒体(電子e-、正孔h+、イオンなど)が電界からの力を受けて瞬時に導体内を移動して導体表面(界面)に移動し、平衡状態となる。界面での電荷密度は、ρ = εdiv E となる(ε:導体の誘電率)。平衡状態では、つぎのような特徴をもつ。
電界 E と電位φのあいだには E = – gradφ の関係があり、導体内部では電界 E = 0 であるので、電位は一定である。
電解では、適用する電位範囲内において、電極反応に関与しない不活性の電解質を添加する。これを支持電解質という。この電解質(正負のイオンに解離)が導電媒体となり、電解液内部の電位は一定となる。イオンは電極・溶液界面に移動し、電極表面の電気二重層が形成される。電荷をもつ活性物質 X+ に対して、支持電解質の濃度が十分に存在しない場合には、一部の X+ が電極界面に移動して偏在することとなる。また、平衡状態でない(電流が流れる)とき、一部の X+ が導電媒体として関与する。これが上記の電気泳動となる。これらの現象を防ぐために、一般的には、活性物質に対して、支持電解質を50倍以上の濃度で添加する。
<作用電極のフェルミ準位と電子移動>
フェルミ・エネルギーに記載しているように、金属結晶の価電子は、フェルミ球の内部から順に充填され、その外表面近傍の電子の一部は熱エネルギーを受けて、自由原子となっている。この電子は十分な熱・光・電界などのエネルギーによって外部へ放出される(前章1.で述べた。)。しかし、フェルミ球内部は価電子が満たされ状態で、外部からの電子を受け入れることができない。一方。フェルミ準位より高い領域は、空の状態(伝導帯)で外部からの電子を受け入れることができる。
<分子X内の電子と井戸型ポテンシャル>
分子Xの価電子(1つと仮定)の状況は、井戸型ポテンシャル内に拘束された電子で説明できる。今、Xの電子は基底状態(n = 0)にあり、X+は全ての準位(n = 0, 1, 2,・・・・)は空の状態とする。水の電位窓(電解条件にもよるが、2V前後)の範囲内で酸化還元に伴う電子エネルギーレベルに対応する井戸型ポテンシャルの深さVoは、EF(仕事関数で示される井戸の深さ)などと比べて浅く、井戸外での波動関数の広がりが大きいことに注目されたい。
< Ee > EF ~ 作用電極 ← 分子 X への電子移動>
図2(A)に示すように、作用電極WEに対して溶液側の電位を負に保つと、Ee > EFとなり、X内の電子がWEの空準位へ移動する。このとき、ΔE = Ee – EF に相当するエネルギーは作用電極の結晶格子の振動エネルギーへ移行し、さらには接している溶媒分子の熱エネルギー(並進、回転、振動エネルギー)と熱的平衡状態になるまで、エネルギー移動が行われる。
なお、Ee < EFでは、WEには価電子が満たされており、移動できる空席がないので電子移動は起こらない。
< Ee < EF 〜 作用電極 → 分子 X+ への電子移動>
図2(C)に示すように、WEの自由電子がX+の空準位(n ≠ 0)に電子が移動できる。しかし、この電子は、低位の準位に遷移して安定化する。この遷移エネルギーは分子 X(aq)の水和水分子の再配置や回転・振動エネルギーへ移行され、最終的には溶媒分子の熱エネルギーへ移行する(緩和)。この緩和過程は、電子移動速度に比べて、十分に遅い速度で進行する。
< Ee = EF 〜 作用電極 ⇆ 分子 X/X+ への電子移動 〜 自然電位>
Ee = EF が等しいとき、電子移動は、X → WE と X+ ← WE の双方向へ同じ速度で進行し、セル外部へ電流は流れない。また、分子X/X+の濃度変化も見られない。このときの電位を自然電位といい、Ee = E° + (RT/F) ln [X+]/[X] (E°: 標準酸化還元電位; [ ]:濃度、活量係数は1とする。)で示す値となる。
なお、前述したように常温では熱エネルギーによって、電極結晶体のフェルミ球表面近傍の内部には価電子の空席、外部には自由電子が存在すること、一方で溶媒分子および分子 X/X+ も熱エネルギーによる揺らぎがあるため、自然電位の測定値にはある程度の幅があるものと推定される。
(c) ミクロ視点での電極反応の意味
作用電極は、電子の受授のみを行いその表面は均一で理想的なものとし、電極そのもの溶出や析出はないものとした。実際には、電極の表面は均一ではなく、その材料によって複雑な現象を示す。詳細については、固体(金属)電子論や電気化学などの専門書・文献を参照されたい。
上記の電極反応は、酸化(電子供与体)と還元(電子受容体)が互いに逆反応となる系を取り上げた。現実には、電子供与体と電子受容体が異なるケースが多い。電極の溶出(腐食など)や電極表面での析出(めっきなど)、電極表面への活性物質の吸着などもある。これらの電極反応は、別ページで取り上げる。
電極反応では、電極表面への活性物質の供給速度(拡散速度)が問題となる。ここでは、電極界面での電子移動反応に影響を与えない十分な供給速度としている。
本章で取り上げたミクロ的なモデルは、電極反応を理解する上で、基礎知識として重要である。さらに、光触媒による難分解性物質の処理などにおいては、固体(半導体)の電子物性と液相物質の関係のミクロ的な理解が必要となる。
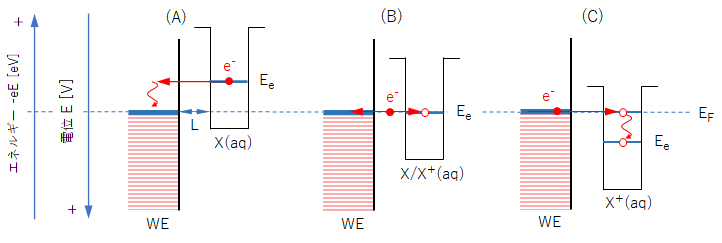
図2 電極電位の制御と電極-溶液界面での電子移動のイメージ図
WE-作用電極、X(aq)-溶解分子X(還元体)、X+(aq)-溶解分子X(酸化体)、
Ef-フェルミ準位、Ee-分子X/X+内の電子エネルギー準位(上記説明では、井戸型ポテンシャルの準位 n = 0 に対応するものとしている。)
L-WEと分子X/X+の井戸型ポテンシャルの近接距離で、エネルギー障壁の厚さ
2.電位の基準と電位差
電界における電位 V と電位差 ΔV も、上記の標高と同じ扱いができる。任意の状態の電位を基準(= 0V)とし、ある状態までの電位差を電位として定めている。エネルギー E も同様に扱っている。
基準が異なれば電位(値)も異なるが、物理的に重要なことは、電位差である。ある状態の電位が他の状態の電位に対してどのくらい「高い」のか、または「低い」のかが重要となる。これは、電位の基準に依らない。さらに、異なる基準間の電位差が既知であれば、相互に基準の異なる電位(値)を変換できる。以上のことから、電位を示すとき、基準となる状態の電位を明記する。ただし、相対的な電位を表すとき、その必要はない。分野が異なれば、同じ対象でも電位の基準が異なる。以下に、その事例を示す。
(1)真空準位
電気伝導体、例えば、金属(T = 0 K)の自由電子(最外殻電子)は全て縮退し、フェルミ準位 Ef(エネルギー)以下にある。したがって、E∞ と Ef(= -φ)との関係から、無限遠の真空電位 V∞(= 0)を基準とするフェルミ電位 Vf = -Ef/e を知ることができる。
気相中での物質間や気相/固相界面での電子移動において、その電子状態をエネルギー準位/電位で示すときには、上記真空準位を基準としている。
(2)基準電極
(3)接地電位
3.電極電位の制御-3電極方式電解セル
(1)作用電極
利用目的により、作用電極の材料、形状、様式が異なる。形状は、線、板、棒など、様式は固定、滴下、回転などがある。
(2)基準電極
標準水素電極 SHE(VRE = 0 V)はH2ガスを用いるため扱いが容易でないので、電極電位が安定な銀-塩化銀電極 Ag-AgCl(VRE = 0.199V vs SHE、飽和KCl、25℃)や飽和カロメル電極SCE(VRE = 0.241V vs SHE)を基準電極として用いることが多い。最近では、SCEは環境に問題があるのでほとんど使われていない。
REとWEとの電位差がVのとき、SHEに対する作用電極WEの電位は VWE = V + VRE となる。
(3)対極
なお、上記1.(2)で述べたように、セル内を流れる電流(観測される電流)が ‘0’ であっても、電極界面での電子の受授(⇄)は常時起こっており、双方向の速度が釣り合っているだけである。目的に応じて作用電極の材料は異なる。対極に求められる性能として、作用電極で行われる電子の放出/受取に対して、余裕を持って対応できる受授(⇄)速度の大きいことが求められる。したがって、対極材料の選定に加えて、その面積を十分大きくしている。
研究試験では、特性のよく分かっている白金 Pt 線/板が用いられるが、規模の大きい実装置ではコストの安いステンレス板などが用いられる。
(4)電解セル内の電位分布と等価回路
電解セルに直流を印加したときの、作用電極から基準電極に至るまでの電位分布とセル全体の等価回路を図4に示す。
図(A)に示す dW、dS、dR は作用電極WEの電気二重層、電解液相、基準電極の電気二重層の厚みで、dW、dR は 10Å 程度、WE の形状や様式によって異なるが、ここでは dS は数mm とする。dS と dR の界面は、RE 液絡部(ガラス管を細工したルギン細管で、例えば、Ag-AgCl 電極では、飽和 KCl 溶液を満たしている)の先端である。
図(B)には、各相(層)の抵抗 Rj、電圧降下(印加電圧)Vj、電流 I の関係を示している。RC と RW は両電極の電気二重層の抵抗、RS は CE-WE間の溶液抵抗である。RS を RE の液絡部先端によって分割し、RW 側の割合β(0<β<1)とすると、RE端部-WE電気二重層までの電圧降下は IβRS = βVS となる。したがって、RE先端部-WE間には電圧 VX = VW + βVS が印加されることとなる。
なお、RE 電極内部の dR 領域には、電気二重層に加えて、ルギン細管液絡溶液の抵抗もあるが、支持電解質の濃度が高いことから、その値はセル溶液の抵抗に比べて小さい。下記測定回路で説明するが、理想的な電気回路では、この部分を流れる電流 ‘i’ = 0 であるので、 RE 領域全体の電圧降下は ‘0’となる。ただし、ルギン細管先端の液絡相と電解液相の界面で、支持電解質の種類と濃度の相違による1mV程度の液間電位差が発生する。液間電位を小さくするため、電解液の支持電解質を基準電極を同じものとするなどの方法があるが、詳細は省略する。
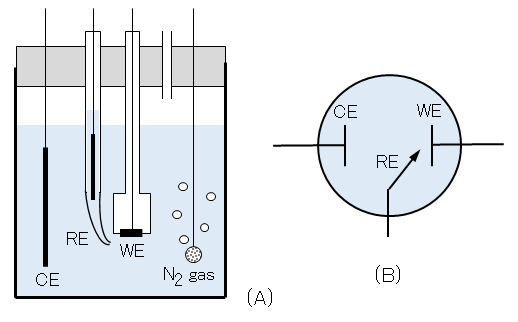
図3 3電極法による実験用電解セル
(A) 実験用電解セルの概略図、(B) 電解セルの模式図; WE-作用電極、RE-基準電極、CE-対電極
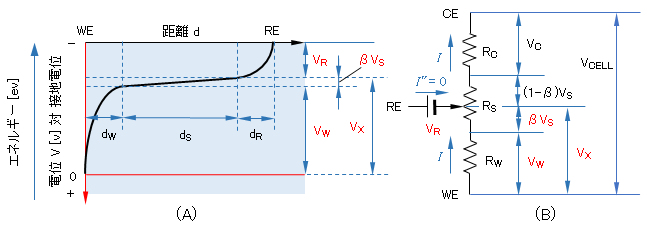
図4 3電極方式の電解セルのイメージ図
(A) 電解セル内の作用電極 WE、溶液 S、基準電極 RE の距離 d と電位 V の関係
dW:WE界面の電気二重層の厚さ、dS:両極間距離から両二重層の厚さを引いたもの、dR:RE界面の電気二重層
(B) 電解セルの等価回路
I-CE-WE間の電流、RC-CE電気二重層の抵抗、RS-溶液抵抗、RW-WE電気二重層の抵抗、VCELL-セル全体への印加電圧、Vj-各抵抗 Rj による電圧降下(= 各抵抗へ印加電圧)、β-溶液抵抗RSの内、RE 液絡部先端から WE 二重層までの電圧降下の割合、VW-WEの二重層へ印加電圧
<電気分解の意義>
一方、電気分解での作用電極の電気二重層の厚さは10 Å程度といわれ、水分子 3 個分に相当する。電気セルには、支持電解質があるので、図5に示すように、外部電圧の大部分は、電気二重層に配分される。電気分解では1V 程度の電圧(CELL全体で数 V)で、作用電極に対して109v/m程度の電界を加えることとなる。このように、気相中の電界放出では、作用電極-対電極の間の電界強度は均一であるのに対し、電解では電極界面の電気二重層に集中されので、印加電圧は前者に比べて極めて小さなものとなる。
<注意事項>
本ページに記載する電解セルおよび測定回路は、交流にも対応ができる。印加電圧に対するセル電流の値および位相が周波数によって異なり、内容が複雑になるので、解説は別ページで取り上げる。交流回路では、溶液抵抗、電気二重層や上記の電極界面での電子受授(⇄)に関する情報が得られる。
4. 3電極方式による電解セルの測定回路
以下、反転入力端子(-)を端子(-)、非反転入力端子(+)を端子(+)と略記し、出力端子はそのままで表記する。以下、回路の各点①~⑧の電位 V を接地電位(= 0V、アース)に対するものとすると、対接地に対する各点①〜⑧の計測電圧 Vは、対接地電位を基準とする各点の電位 Vを示すこととなるので、以下の記述では、電位と電圧は同じものとして扱う。なお、下記の内容は図3および図4に対応しているので、関連づけて理解されたい。
OP3は端子(+)は接地してあるので、その端子(-)は仮想接地されている。したがって、作用電極① WE の電位は ’0 V’ となる。
(1)溶液電位の制御
一方で、電極電位を制御する外部電源 G からの入力電圧⑦ Vi は抵抗 R1 を通して、端子(+)を接地したOP1の端子(-)に接続している。この電流 i は回路⑤を経て、回路③に流れ込む。⑦→⑤および⑤→③の間の抵抗は同じ値 R1 であるので、CELLを流れる電流 I がどのような値であっても、REの液絡部先端にある溶液②の電位(対接地電位)を、
(VX + VR) = – Vi (1)
に保つようにOP1アンプが作動する(反転増幅回路)。このとき、OP1の出力電圧は
VCELL = I(RC + RS + RW) (2)
となる。
(2)CELL電流の計測
(3)表示器への電圧値と電流値の出力
(4)溶液抵抗による電圧降下の補償
OP3の出力電圧⑧ Vo をポテンショメーター P で分割した電圧 αVo = αIRx(0 ≦ α ≦ 1)をOP4でインピーダンス変換して抵抗 R1 を介してOP1の端子(-)に返す。OP1に対して、OP2回路は負帰還、OP4は正帰還となる。
RSはあらかじめ測定しておく必要があるが、βVS = βIRS ≒ αIRx = αVo となると、測定回路が発振するので、その直前の値に設定する。回路③と④は加算回路で、
Vi = (i – i’)R1 = – (VX + VR – i’R1) = – (VX + VR – βVS) (3)
となり、溶液②には溶液抵抗による電圧降下 -βVS が加算された電圧が溶液②に印加されることとなる。これは、OP4の入力④と出力④の電圧は同じであるので、
i’R1 = αIRX = βIRS = βVS (4)
となるからである。
以上のことから、図4に示す電位の関係から、
VW = VX – βVS = – (Vi + VR) (5)
となる。VRは基準電極の電位であるので、標準水素電極SHEを用いれば、VR = 0 Vであるので、VW = – Vi となる。他の電極 REを基準として用いれば、Vi にVR(対SHE)を加算した電圧が図5(A)のdW(WEの電気二重層)に印加されることとなる。
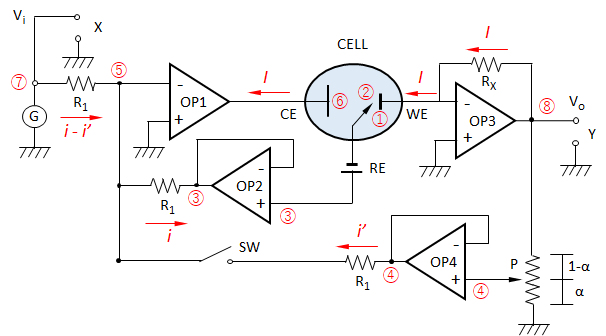
図5 3電極方式の電解セルと基本測定回路(電位規制用)
CELL-電解セル、WE-作用電極、CE-対極、RE-基準電極、X-作用電極への印可電圧の表示用出力端子、Y-セル電流の表示用出力端子、
G-作用電極への印可電圧発生器、OP1-電解セルへの電圧印可用OPアンプ、OP2-溶液電位の測定用OPアンプ、OP3-セル電流測定用OPアンプ、OP4-溶液抵抗補償用OPアンプ
(5)セル電流の制御と基本回路
図5に示す電位規制回路のWE①のリード線をOP1の端子(-)に接続して、負帰還する。外部から入力した直流電源電圧に対して、⑦→⑤に設置した抵抗を通して、電流 I = Vi/Rx が流れる。OP1は、⑤→①→⑥を巡回して、同じ値の電流 I が帰還するように作動する。
電流を規制する電圧 Vi および Vo(REに対するWE電位)を記録計やデジタル表示器の入力 X 端子、入力 Y 端子に接続する。
規制する電流レンジに対応して抵抗 Rx を切り替える。また、電流 I が微少で Vo が小さい場合には、これを増幅するか、表示器のレンジを切り替えて適切な電圧になるように調整する。
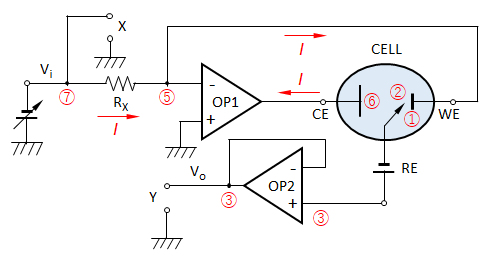
図6 3電極方式の電解セルと基本測定回路(電流規制用)
OP1-セル電流規制用OPアンプ、他:図5と同じ
<注意事項>
各装置・計器の設計・製作において、各デバイスや部品の一端をアースに接続し、必要に応じて他デバイスや部品との接続はそれぞれの信号につき、1本のリード線でよいので、回路配線が簡略化される。また、装置・計器の接続ミスを防ぐことができる。さらに、内部回路の各点の状況をチェックするときは、計測器の(-)端子をアースに接続し、(+)端子を各点に接触させればよいので簡便である。
電解セルの実回路では、作用極を仮想接地して、そのフェルミ準位(電位表示)を接地電位に保持しているので、基準電極の電位や溶液中の活性物質の電位が相対的に変化することとなる(例えば、図2)。一方で、基準電極電位を電位基準とすれば、フェルミ準位が相対的に変化することとなる。電気化学分野の書籍・解説では、後者の立場で記述されているが、本ページでは前者の立場で解説しているので、注意されたい。
Appendix
電気化学測定に用いられるOPアンプの主な回路事例について、説明する。
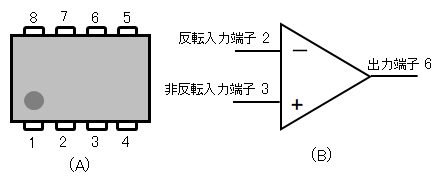
図A1 OPアンプの形状と略表記の事例
(A)形状とピン配置:1ーOffset Trim, 2ーInput(-), 3ーInput(+), 4ーV(-), 5ーNC, 6ーOutput, 7ーV(+), 8ーOffset Trim; V:電源
(B)オペレーションアンプの略表記
(1)OPアンプの特徴
OPアンプの特徴として、①超高入力インピーダンス、②超低出力インピーダンスで、③2つの入力端子間は絶縁されているが、同じ電位に保たれる。ここで説明するOPアンプは理想的なもので、その入力インピーダンス Zi = ∞、出力インピーダンス Zo = 0、入力と出力に位相差が生じないもの(無限大の応答速度)として、図A2に示す代表的な応用回路を説明する。
(2)反転増幅回路
図A2(A)は反転増幅回路と呼ばれ、入力端子(+)が接地されている。入力端子(-)に抵抗R1、入力端子(-)と出力端子の間に抵抗R2がそれぞれ接続されている。この回路の抵抗Riに電圧Vo(出力インピーダンスは’0’である。)が入力されると、I = V/R1の電流が流れる。
端子(-)と端子(+)は、前節(1)③で述べたように、絶縁しているが同電位であり、端子(+)が接地されているので、端子(-)の電位は’0[V]’となる。これを仮想接地という。前節(1)①で述べたように、端子(-)の入力インピーダンスは’∞’であるので、抵抗R2に対して、R1から流出する電流’I’の全てが流れ込む。
以上のことから、Vo = -R2I = -(R2/R1)Vi となり、入力電圧はR2/R1の比率で増幅され、正負が反転された出力インピーダンス’0’の電圧Voが出力される。
(3)加算回路
図A2(B)は加算回路といわれ、同じ値の抵抗Rが入力端子(-)に並列に2個、入力端子(-)と出力端子の間に1個、それぞれ接続された回路である。
前節(2)で説明した理由から、Vo = -R(I1 + I2) = -(Vi1 + Vi2)となり、入力電圧の加算された電圧が出力される。ただし、電圧の正負が反転される。
(4)電圧測定回路
図A2(C)の回路は電圧測定に用いられる。端子(+)と端子(-)は、絶縁されているが同じ電位であり、端子(-)と出力端子は直結しているので、入力電圧と出力電圧は全く同じ値(符号も同じ)となる。加えて、入力端子(+)は入力インピーダンスが’∞’であるので、測定対象となる系から全く電流を取り出すことなく、その電圧を測定できる上に、出力インピーダンスは’0’である。このことから、この回路は入出力インピーダンス変換回路とも言われる。
(5)電流測定回路
図A2(D)の回路は、電流測定に用いられる。入力端子(-)と出力端子の間に抵抗R2が接続されている。端子(-)に電流 I が流れ込むと、Vo = -RxI に等しい電圧が出力する。出力電圧が記録計やデジタル計の入力レンジに適合するように、その入力レンジに応じて、抵抗Rxのレンジ(Rxi)を切り替える。
微少電流に対しては、抵抗Rxが大きくなり、電磁誘導電流が流れて雑音が生じるので、測定系(電解セル、リード線、電流測定回路等)は電磁シールドするなどの対策が必要である。
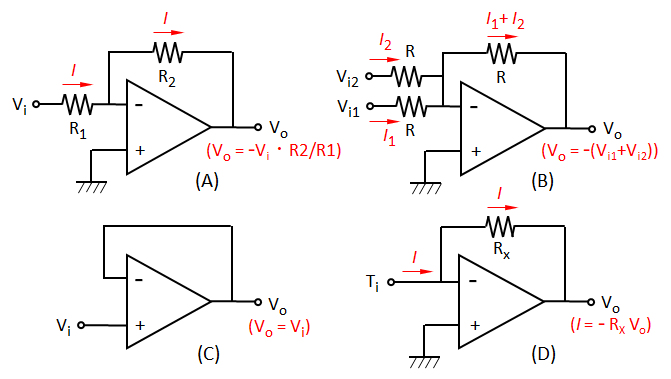
図A2 オペレーションアンプを用いた応用回路の事例
(A)反転増幅回路、(B)加算回路、(C)電圧測定回路、(D)電流測定回路
掲載日:2018年5月26日
更新日:2018年6月16日
