村上定瞭(水浄化フォーラム)
○ ミクロ粒子の波動関数 H
○ よい量子数、結晶中伝導電子、結晶格子 C
○ 井戸型ポテンシャル W
○ トンネル効果 T
○ 調和振動子 O
○ ミクロ粒子の統計力学 S
○ フェルミ・エネルギー F
○ 金属電子 M
○ 光子エネルギーと粒子測定 P
○ 宇宙誕生と物質生成
○ プラズマ
○ よい量子数、結晶中伝導電子、結晶格子 C
○ 井戸型ポテンシャル W
○ トンネル効果 T
○ 調和振動子 O
○ ミクロ粒子の統計力学 S
○ フェルミ・エネルギー F
○ 金属電子 M
○ 光子エネルギーと粒子測定 P
○ 宇宙誕生と物質生成
○ プラズマ
(注)「ミクロ世界」の内容は複数ページに分割されいるが、目次は共通となっている。
水浄化技術の中には、「ミクロ世界ー素粒子」に係る基礎知識が必要な事項もある。本サイトの他ページにおいて、リンク説明が必要なミクロ世界の現象について、適宜、加筆する(更新年月日に留意)。本サイトの編集者は物理学分野の知識が浅いので、不適切あるいは誤った記述もある。閲覧者から、ご指摘を賜れば、幸いである。
なお、本ページの目的は、ミクロ粒子(電子、原子、分子、光子など)の挙動に関する数理学な手法や解析の解説ではなくて、(境界)条件下における解(結果)の定性的な意味を理解し、関係する水浄化技術(浄化装置の原理・設計やその運転管理、水質分析の原理・装置・方法など)の理解を深めることにある。詳しい数理学的な解析や手法は、それぞれの分野の専門書を参考とされたい。
なお、本ページの目的は、ミクロ粒子(電子、原子、分子、光子など)の挙動に関する数理学な手法や解析の解説ではなくて、(境界)条件下における解(結果)の定性的な意味を理解し、関係する水浄化技術(浄化装置の原理・設計やその運転管理、水質分析の原理・装置・方法など)の理解を深めることにある。詳しい数理学的な解析や手法は、それぞれの分野の専門書を参考とされたい。
フェルミ・エネルギー
(1)箱に閉じ込められた電子
今、電子を一辺Lの立方体の箱の中に閉じ込めたとき、3次元空間における時間に依存しない電子の波動関数は、一般に、つぎのように示される。
ψ(x, y, z) = (1/√V)exp(iκ・r)
κ = (2π/L)(nx, ny, nz) (F-1)
E(κ) = (ħ2/2m)(2π/L)2(nx2 + ny2 + nz2)
= (ħ2/2m)κ2
ni = 0, ±1, ±2,・・・
κ:波数ベクトル
E(κ):量子化されたκに対する固有エネルギー
ψ(x, y, z) = (1/√V)exp(iκ・r)
κ = (2π/L)(nx, ny, nz) (F-1)
E(κ) = (ħ2/2m)(2π/L)2(nx2 + ny2 + nz2)
= (ħ2/2m)κ2
ni = 0, ±1, ±2,・・・
κ:波数ベクトル
E(κ):量子化されたκに対する固有エネルギー
(2)フェルミ球
式(F-1)で示される3次元κ空間において、電子のエネルギー状態は量子数の組(nx, ny, nz)で示される。パウリの原理によれば、これにスピン量子数 s(= ±1/2)を加えた量子数の組(nx, ny, nz, s) に2つ以上の電子が占めることはできない。一般に外部磁場がないときには、sで示されるエネルギーは、ni (i = x, y, z) で示されるエネルギーに比べて無視できる程度であるので、上記κ空間での各エネルギー状態にスピン±1/2の電子2個が入ることができる。
T = 0 Kでは、エネルギー状態の組(nx, ny, nz) に対し、エネルギーの最も低い量子状態から順に、スピン ±1/2(↑,↓)の電子2個ずつを詰めていく。具体的には、(0, 0, 0)、(1, 0, 0)、(0, 1, 0)、(0, 0, 1)、(-1, 0, 0)、(0, -1, 0)、(0, 0, -1)、(2, 0, 0)、・・・と詰めていく様子を図F1に示す。
ここで、1モルの1価金属を例にとれば、NA = 6 ×1023個の電子をκ空間(逆格子空間ともいう:長さの単位が実空間の逆数)に詰めていくこととなり、電子を詰めた半径κFの球を形成する。これをフェルミ球という。ここで、留意すべきこととして逆格子空間が一辺 2π/Lの立方格子を単位とする不連続な“量子点”から成り立っていることである。。
一例を上げると、Cu 1モルの重量は63.55 gで、密度8.93 g/cm3であるので、実空間の立方体塊の一辺は、L = 1.92 [cm = 108Å] 、である。一方、κ空間の逆格子の1辺は、2π/L = 3.37-8[Å-1]、となる。
T = 0 Kでは、エネルギー状態の組(nx, ny, nz) に対し、エネルギーの最も低い量子状態から順に、スピン ±1/2(↑,↓)の電子2個ずつを詰めていく。具体的には、(0, 0, 0)、(1, 0, 0)、(0, 1, 0)、(0, 0, 1)、(-1, 0, 0)、(0, -1, 0)、(0, 0, -1)、(2, 0, 0)、・・・と詰めていく様子を図F1に示す。
ここで、1モルの1価金属を例にとれば、NA = 6 ×1023個の電子をκ空間(逆格子空間ともいう:長さの単位が実空間の逆数)に詰めていくこととなり、電子を詰めた半径κFの球を形成する。これをフェルミ球という。ここで、留意すべきこととして逆格子空間が一辺 2π/Lの立方格子を単位とする不連続な“量子点”から成り立っていることである。。
一例を上げると、Cu 1モルの重量は63.55 gで、密度8.93 g/cm3であるので、実空間の立方体塊の一辺は、L = 1.92 [cm = 108Å] 、である。一方、κ空間の逆格子の1辺は、2π/L = 3.37-8[Å-1]、となる。
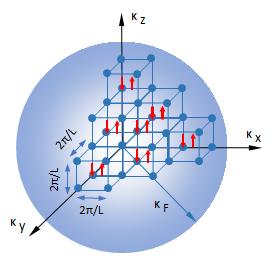
図F1 フェルミ球の構築
1辺が2π/Lの逆単位格子の中に、2個ずつ価電子を内部格子から順に詰めていく。
(3)フェルミ・エネルギー
Cuの1モル・フェルミ球(半径κF)にはNA個の電子が存在し、体積(2π/L)3あたり2(= g)個の電子を詰めるので、つぎの関係が成り立つ。
(2π/L)3 : 2 = (4πκF3) : NA
L3 = V とおくと、フェルミ球の半径κFは
κF = [3π2(NA/V)]1/3 (F-2)
を得る。V = 63.55[g]/8.93[g/cm3] = 7.12[(108Å)3]を式(F-2)に代入すると、κF = 1.36[Å-1]となる。κF ≫ 2π/Lであるので、逆格子空間はほど連続した量子点の集合とみることができ、フェルミ面は滑らかな球面とみることができる。
フェルミ半径に等しい波数をもつ電子エネルギーは、式(F-1)に式(F-2)を代入して、
EF = (ħ2/2m)kF2 = (ħ2/2m) = [3π2(NA/V)]2/3 (F-3)
=36.46(NA/V)2/3 [eV] (Vの単位をÅ3で示すとき)
EFとNAの添え字を取り去ると、この式は体積VあたりN個の価電子をエネルギーの低い順に詰めたとき、その最大エネルギーEを示している。式(F-3)を変形して、次式を得る。
N(E) = dN/dE = [V/(2π)2](2m/ħ2)3/2√E (F-4)
N(E)は電子の状態密度といわれ、N(E)ΔEはE~E+ΔEにある電子数を表す。図F2にEとN(E)の関係を示す。したがって、エネルギーが0~EFまでの電子の総数は次式で示される。
N = ∫N(E)dE (0~EFの範囲で積分) (F-5)
(2π/L)3 : 2 = (4πκF3) : NA
L3 = V とおくと、フェルミ球の半径κFは
κF = [3π2(NA/V)]1/3 (F-2)
を得る。V = 63.55[g]/8.93[g/cm3] = 7.12[(108Å)3]を式(F-2)に代入すると、κF = 1.36[Å-1]となる。κF ≫ 2π/Lであるので、逆格子空間はほど連続した量子点の集合とみることができ、フェルミ面は滑らかな球面とみることができる。
フェルミ半径に等しい波数をもつ電子エネルギーは、式(F-1)に式(F-2)を代入して、
EF = (ħ2/2m)kF2 = (ħ2/2m) = [3π2(NA/V)]2/3 (F-3)
=36.46(NA/V)2/3 [eV] (Vの単位をÅ3で示すとき)
EFとNAの添え字を取り去ると、この式は体積VあたりN個の価電子をエネルギーの低い順に詰めたとき、その最大エネルギーEを示している。式(F-3)を変形して、次式を得る。
N(E) = dN/dE = [V/(2π)2](2m/ħ2)3/2√E (F-4)
N(E)は電子の状態密度といわれ、N(E)ΔEはE~E+ΔEにある電子数を表す。図F2にEとN(E)の関係を示す。したがって、エネルギーが0~EFまでの電子の総数は次式で示される。
N = ∫N(E)dE (0~EFの範囲で積分) (F-5)
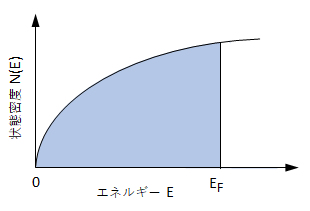
図F2 金属結晶の価電子の状態密度分布 (T = 0 K)
T = 0 K において、結晶中の価電子は全てフェルミ・エネルギー EF 以下の状態を占めている。
代表的な金属について、式(F-3)を用いてフェルミエネルギーを計算した値を表F1に示す。なお、Ωは1原子あたりの体積Vを示す。例えば、bcc金属Naの格子定数は4.22Åであるので、Ω = (4.22)3/2 = 37.7Å3となる(結晶構造 bcc の単位格子に2個の原子が存在する。)。Naは1価原子であるので、1原子あたりN = 1 となる。これらの定数を式(F-3)に代入すると、EF = 3.2 eVが得られる。
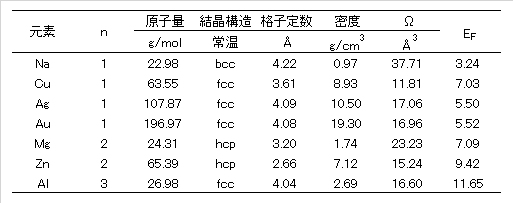
文献[水谷, 1995]より転記
(以下、執筆中)
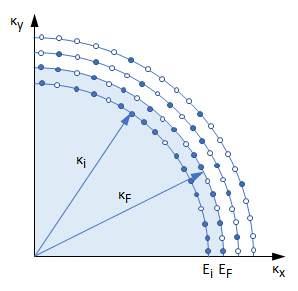
図F3 有限温度(T ≠ 0 K)におけるフェルミ球の1/4断面
●:電子が占有しているフェルミ格子、○:電子が空席のフェルミ格子
フェルミ球(薄青色の領域)内の空席○数とフェルミ球外の占有席●数は等しい
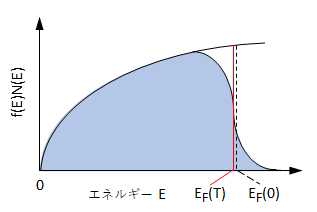
図F4 有限温度における金属結晶の価電子の状態密度分布(T ≠ 0 K)
目次へ
金属電子
フェルミ粒子の気体として縮退を示す重要な例として金属内部の電子がある。金属が電気をよく伝えることや熱すると表面から電子が飛び出す事実は、金属内で電子がかなり自由に運動していることを暗示する。金属をつくる原子は、その最外殻電子がその結晶中を運動するものとするとその特性がよく説明できる。ちょうどその金属の中に閉じ込められた気体のようなものである。
ここでは、金属電子の挙動について、量子力学と統計力学の視点から、数例を解説する。
ここでは、金属電子の挙動について、量子力学と統計力学の視点から、数例を解説する。
宇宙の誕生と物質の生成
<ビッグバンの膨張と原子の生成>
宇宙誕生のビッグバン(BG)から少し(10-11s)たつと素粒子ができはじめる。そのときの宇宙の温度は1015Kで、レプトン、クオーク、グルーオン、光子などが生成する。
さらに、BGから10-4sくらいたつと、宇宙の温度は1012Kくらいになり、陽子や中性子もできる。そして、BGから1分後、宇宙は109Kくらいまで下がり、He、Li、Beなどといった軽い元素の原子核も存在できるようになる。
BGから数十万年後、宇宙はさらに膨張し、その温度は数103Kまでに下がると、原子核が電子を捉えて電気的に中性な原子をつくることができるようになる。量的にはH原子がもっとも多く、ついでHe原子である。これらは、現在の我々自身やまわりの様々な元素を構成する元となっっている。
このころの宇宙では、原子核・電子・光子がばらばらに混在していた状態(プラズマ)から脱して、光子は自由電子と反応して直進できない状態であったが、自由電子が原子核に捕捉されて中性の原子が生成さるようになると、光子は宇宙空間を自由に放射されることとなる。いわゆる宇宙の晴れ上がりである。
宇宙誕生のビッグバン(BG)から少し(10-11s)たつと素粒子ができはじめる。そのときの宇宙の温度は1015Kで、レプトン、クオーク、グルーオン、光子などが生成する。
さらに、BGから10-4sくらいたつと、宇宙の温度は1012Kくらいになり、陽子や中性子もできる。そして、BGから1分後、宇宙は109Kくらいまで下がり、He、Li、Beなどといった軽い元素の原子核も存在できるようになる。
BGから数十万年後、宇宙はさらに膨張し、その温度は数103Kまでに下がると、原子核が電子を捉えて電気的に中性な原子をつくることができるようになる。量的にはH原子がもっとも多く、ついでHe原子である。これらは、現在の我々自身やまわりの様々な元素を構成する元となっっている。
このころの宇宙では、原子核・電子・光子がばらばらに混在していた状態(プラズマ)から脱して、光子は自由電子と反応して直進できない状態であったが、自由電子が原子核に捕捉されて中性の原子が生成さるようになると、光子は宇宙空間を自由に放射されることとなる。いわゆる宇宙の晴れ上がりである。
<宇宙密度のゆらぎによる核融合と重い原子の誕生>
宇宙空間は、まったく均一・一様ではなく、密度の高い場所や低い場所といったゆらぎが生じる。少しでも密度の高い場所は、その引力によってHやHe原子を集め、ますます密度が高くなる。密度の高い場所は、ますますこれらの軽い原子ガスを集め、中心部の温度・圧力は次第に上昇する。原子は原子核と電子がばらばらになったプラズマという状態になる。
中心部の温度107Kに達すると、むき出しになったHの原子核(+)が激しく衝突し、Heの原子核を生成する核融合反応が起こる。これが恒星の誕生である。核融合反応が起こると、融合反応による熱と恒星自身のつくる縮もうとする重力が釣り合って安定な状態になる。
最初Heは核反応しないが、自身の力で収縮する。重い恒星では、その中心部の温度・圧力はさらに上がり、HeがCやOになる核融合反応がはじまる。CやOで構成される中心部の温度・圧力が増すと、より重いNeやMg、さらにSiといった具合に、だんだんと重い原子の原子核が各融合反応によって合成されていく。
宇宙空間は、まったく均一・一様ではなく、密度の高い場所や低い場所といったゆらぎが生じる。少しでも密度の高い場所は、その引力によってHやHe原子を集め、ますます密度が高くなる。密度の高い場所は、ますますこれらの軽い原子ガスを集め、中心部の温度・圧力は次第に上昇する。原子は原子核と電子がばらばらになったプラズマという状態になる。
中心部の温度107Kに達すると、むき出しになったHの原子核(+)が激しく衝突し、Heの原子核を生成する核融合反応が起こる。これが恒星の誕生である。核融合反応が起こると、融合反応による熱と恒星自身のつくる縮もうとする重力が釣り合って安定な状態になる。
最初Heは核反応しないが、自身の力で収縮する。重い恒星では、その中心部の温度・圧力はさらに上がり、HeがCやOになる核融合反応がはじまる。CやOで構成される中心部の温度・圧力が増すと、より重いNeやMg、さらにSiといった具合に、だんだんと重い原子の原子核が各融合反応によって合成されていく。
<超新星爆発とFeより重い元素の生成>
恒星内部の核融合反応は発熱反応であるが、それによって生成する元素はFeまでである。Feより重い元素の融合は吸熱反応で、それらの核は分裂するときにのみエネルギーを放出する。したがって、Feの原子核はもっとも安定な核といえる。だから、恒星の中心部に鉄の原子核ができてくると、それ以上の核反応は起こらず、Feの原子核は増えて貯まる一方となる。ある程度はまわりからの重さに耐えられるが、Feで構成される中心部での核反応は停止しているので、その芯では膨張する力は生じない。まわりからの重さが限界に達すると、中心自身が崩壊し、その反動で恒星は大爆発する。これが超新星(Ⅱ型)である。このときのほぼ一瞬の爆発で、太陽が50億年かかって放出したエネルギー以上のエネルギーを放出する。
この膨大なエネルギーで、ふつうの恒星内部で生成されないFeよりも重い元素が合成される。この超新星爆発で吹き飛ばされた元素(軽い元素およびFeより重い元素)を材料に、再び新しい恒星や惑星がつくられることになる。
恒星内部の核融合反応は発熱反応であるが、それによって生成する元素はFeまでである。Feより重い元素の融合は吸熱反応で、それらの核は分裂するときにのみエネルギーを放出する。したがって、Feの原子核はもっとも安定な核といえる。だから、恒星の中心部に鉄の原子核ができてくると、それ以上の核反応は起こらず、Feの原子核は増えて貯まる一方となる。ある程度はまわりからの重さに耐えられるが、Feで構成される中心部での核反応は停止しているので、その芯では膨張する力は生じない。まわりからの重さが限界に達すると、中心自身が崩壊し、その反動で恒星は大爆発する。これが超新星(Ⅱ型)である。このときのほぼ一瞬の爆発で、太陽が50億年かかって放出したエネルギー以上のエネルギーを放出する。
この膨大なエネルギーで、ふつうの恒星内部で生成されないFeよりも重い元素が合成される。この超新星爆発で吹き飛ばされた元素(軽い元素およびFeより重い元素)を材料に、再び新しい恒星や惑星がつくられることになる。
プラズマ
<プラズマとは>
温度が上昇すると、物質は固体から液体に、液体から気体にと状態が変化する。気体の温度が上昇すると気体の分子は解離して原子になり、さらに温度が上昇すると原子核のまわりを回っていた電子が原子から離れて、正イオンと電子に分かれる。この現象は電離とよばれる。電離によって生じた荷電粒子を含む気体をプラズマとよぶ。
温度が上昇すると、物質は固体から液体に、液体から気体にと状態が変化する。気体の温度が上昇すると気体の分子は解離して原子になり、さらに温度が上昇すると原子核のまわりを回っていた電子が原子から離れて、正イオンと電子に分かれる。この現象は電離とよばれる。電離によって生じた荷電粒子を含む気体をプラズマとよぶ。
<自然界のプラズマ>
自然界には,地球のエネルギーの源である太陽、それから吹き出す太陽風、地球を取り巻く電離層、極地の空を彩るオーロラ、真夏の積乱雲から走る稲妻など、様々な形のプラズマが存在している。また夜空にちりばめられた数々の恒星に加 えて、星と星との間の空間にも希薄なプラズマが広がっており、宇宙を構成する物質の99%以上がプラズマであるといわれている。
自然界には,地球のエネルギーの源である太陽、それから吹き出す太陽風、地球を取り巻く電離層、極地の空を彩るオーロラ、真夏の積乱雲から走る稲妻など、様々な形のプラズマが存在している。また夜空にちりばめられた数々の恒星に加 えて、星と星との間の空間にも希薄なプラズマが広がっており、宇宙を構成する物質の99%以上がプラズマであるといわれている。
<プラズマと中性気体>
プラズマと通常の中性気体との大きな違いは、荷電粒子の間にクーロン力が働くことである。中性気体では2つの粒子が極めて接近したときだけ粒子間に力が働くのに対して、クーロン力ははるかに遠方まで力をおよぼす。そのため、1つの粒子の運動は多くの粒子に影響をおよぼし、中性気体にはみられない様々な現象が現れる。
プラズマと通常の中性気体との大きな違いは、荷電粒子の間にクーロン力が働くことである。中性気体では2つの粒子が極めて接近したときだけ粒子間に力が働くのに対して、クーロン力ははるかに遠方まで力をおよぼす。そのため、1つの粒子の運動は多くの粒子に影響をおよぼし、中性気体にはみられない様々な現象が現れる。
<電気的中性>
プラズマ中の荷電粒子は、原子に束縛されていた電子がエネルギーを得て電離することによって生じたものである。そのため、粒子のもつ運動エネルギーは粒子間に働くクーロン力のポテンシャルエネルギーよりも大きいのが普通である。また、粒子損失がなければ、プラズマ中の電子のもつ電荷の総和と正イオ ンのもつ電荷の総和は符号が逆で大きさは等しいので、全体としてほぼ電気的中性となっている。電子ビームやイオンビームのように電気的中性条件を満たしていな い荷電粒子系は、通常プラズマとはいわない。
プラズマ中の荷電粒子は、原子に束縛されていた電子がエネルギーを得て電離することによって生じたものである。そのため、粒子のもつ運動エネルギーは粒子間に働くクーロン力のポテンシャルエネルギーよりも大きいのが普通である。また、粒子損失がなければ、プラズマ中の電子のもつ電荷の総和と正イオ ンのもつ電荷の総和は符号が逆で大きさは等しいので、全体としてほぼ電気的中性となっている。電子ビームやイオンビームのように電気的中性条件を満たしていな い荷電粒子系は、通常プラズマとはいわない。
<様々なプラズマ>
通常の気体は常温ではほとんど電離していない。もっとも身近にあるプラズマとしては、ほんのわずかしか電離していないが、蛍光灯やガス炎があげられる。
地球上では粒子密度が高いため電離しにくいので、高度が増すにつれて電離する割合が増加する。これは太陽からの紫外線やX線により電離が増えることと、粒子密度の減少により再結合によって中性原子に戻る機会が減ることによる。そのため高度100kmあたりで電子密度が極大となり、電離層とよ ばれている。高度約300 km 以上の領域は磁気圏とよばれ、さらに電離しやすくなるが、粒子密度が減少するため電子密度はゆるやかに減少する。磁気圏の外側の境界は、太陽からのプラズマの流れ(太陽風)と地球磁場との釣り合いで定まっている。太陽風には、太陽から吹き出されたエネルギーの高い荷電粒子が含まれている。太陽風の届かない惑星間のプラズマは密度も温度も低いものであるが,その量が非常に多いため、宇宙にある物質の99.9%以上がプラズマであるといわれている。
高エネルギー荷電粒子の流れである太陽風を生み出す太陽は,それ自身完全に 電離したプラズマである。太陽の中心部では 4つのH原子からHeを生成する核融合反応によってエネルギーが生成されている。地球上での核融合反応によってエネルギーを生成しようとする試みにおいても、非常に高い温度のプラズマを閉じ込める必要があり、プラズマの性質を調べるための実験的あるいは理論的研究が先進各国で進められている。
もう一つの身近なプラズマの例は固体中の自由電子である。固体中ではイオンは動くことができないが、自由電子は正イオンの強いクーロン力の働く場の中の一成分プラズマとして振る舞うことができる。ただし、粒子密度が非常に高いため、フェルミ温度が実際の温度よりも高くなり、量子力学的な縮退効果が重要な役割を果たしている。
通常の気体は常温ではほとんど電離していない。もっとも身近にあるプラズマとしては、ほんのわずかしか電離していないが、蛍光灯やガス炎があげられる。
地球上では粒子密度が高いため電離しにくいので、高度が増すにつれて電離する割合が増加する。これは太陽からの紫外線やX線により電離が増えることと、粒子密度の減少により再結合によって中性原子に戻る機会が減ることによる。そのため高度100kmあたりで電子密度が極大となり、電離層とよ ばれている。高度約300 km 以上の領域は磁気圏とよばれ、さらに電離しやすくなるが、粒子密度が減少するため電子密度はゆるやかに減少する。磁気圏の外側の境界は、太陽からのプラズマの流れ(太陽風)と地球磁場との釣り合いで定まっている。太陽風には、太陽から吹き出されたエネルギーの高い荷電粒子が含まれている。太陽風の届かない惑星間のプラズマは密度も温度も低いものであるが,その量が非常に多いため、宇宙にある物質の99.9%以上がプラズマであるといわれている。
高エネルギー荷電粒子の流れである太陽風を生み出す太陽は,それ自身完全に 電離したプラズマである。太陽の中心部では 4つのH原子からHeを生成する核融合反応によってエネルギーが生成されている。地球上での核融合反応によってエネルギーを生成しようとする試みにおいても、非常に高い温度のプラズマを閉じ込める必要があり、プラズマの性質を調べるための実験的あるいは理論的研究が先進各国で進められている。
もう一つの身近なプラズマの例は固体中の自由電子である。固体中ではイオンは動くことができないが、自由電子は正イオンの強いクーロン力の働く場の中の一成分プラズマとして振る舞うことができる。ただし、粒子密度が非常に高いため、フェルミ温度が実際の温度よりも高くなり、量子力学的な縮退効果が重要な役割を果たしている。
<広い密度と温度の領域>
以上に述べた代表的なプラズマの電子密度と温度を下図に示す。プラズマの密度と温度の領域は非常に広いことが分かる。密度に至っては25桁の差があるにもかかわらず、プラズマとして数多くの共通な性質をもっているのは、驚くべきことである。
(以上の文章は、京都大学大学院・原子核工学専攻・核エネルギー物理工学研究グループ(村上 定義 教授)のホームページを引用しました。)
以上に述べた代表的なプラズマの電子密度と温度を下図に示す。プラズマの密度と温度の領域は非常に広いことが分かる。密度に至っては25桁の差があるにもかかわらず、プラズマとして数多くの共通な性質をもっているのは、驚くべきことである。
(以上の文章は、京都大学大学院・原子核工学専攻・核エネルギー物理工学研究グループ(村上 定義 教授)のホームページを引用しました。)
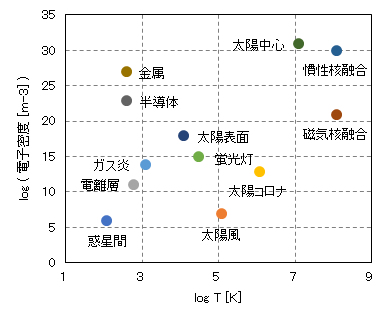
図 代表的なプラズマの温度と電子密度
目次へ
参考文献
E. Merzbacher, 1970: Quantum Mechanics, John Wiley & Sons.
K.S. Pitzer, 1963: Quantum Chemistry, Prentice-Hall.
C.A. Wert & R.M. Thomson, 1970: Physics of Solids, McGraw-Hill.
安達 健五 監修、1969: 金属の電子論 1、アグネ.
市村 浩、1968: 統計力学、裳華房.
久保 亮吾、1934: 統計力学、共立全書.
為近 和彦、2008: 熱・統計力学、北森出版.
沼居 貴陽、2007: 固体物性入門、森北出版.
広江 克彦、2015: 趣味で量子力学、理工図書.
水谷 宇一郎、1995: 金属電子論(上)、内田老鶴圃.
渡辺 正・中林誠一郎、1996: 電子移動の化学―電気化学入門、朝倉書店.
渡辺 正義・米屋 勝利、2002: 物質科学入門、化学同人.
掲載日:2018年05月26日
更新日:2018年12月14日
