村上定瞭(水浄化フォーラム)
○ ミクロ粒子の波動関数 H
○ よい量子数、結晶中伝導電子、結晶格子 C
○ 井戸型ポテンシャル W
○ トンネル効果 T
○ 調和振動子 O
○ ミクロ粒子の統計力学 S
○ フェルミ・エネルギー F
○ 金属電子 M
○ 光子エネルギーと粒子測定 P
○ 宇宙誕生と物質生成
○ プラズマ
○ よい量子数、結晶中伝導電子、結晶格子 C
○ 井戸型ポテンシャル W
○ トンネル効果 T
○ 調和振動子 O
○ ミクロ粒子の統計力学 S
○ フェルミ・エネルギー F
○ 金属電子 M
○ 光子エネルギーと粒子測定 P
○ 宇宙誕生と物質生成
○ プラズマ
(注)「ミクロ世界」の内容は複数ページに分割されいるが、目次は共通となっている。
水浄化技術の中には、「ミクロ世界ー素粒子」に係る基礎知識が必要な事項もある。本サイトの他ページにおいて、リンク説明が必要なミクロ世界の現象について、適宜、加筆する(更新年月日に留意)。本サイトの編集者は物理学分野の知識が浅いので、不適切あるいは誤った記述もある。閲覧者から、ご指摘を賜れば、幸いである。
なお、本ページの目的は、ミクロ粒子(電子、原子、分子、光子など)の挙動に関する数理学な手法や解析の解説ではなくて、(境界)条件下における解(結果)の定性的な意味を理解し、関係する水浄化技術(浄化装置の原理・設計やその運転管理、水質分析の原理・装置・方法など)の理解を深めることにある。詳しい数理学的な解析や手法は、それぞれの分野の専門書を参考とされたい。
なお、本ページの目的は、ミクロ粒子(電子、原子、分子、光子など)の挙動に関する数理学な手法や解析の解説ではなくて、(境界)条件下における解(結果)の定性的な意味を理解し、関係する水浄化技術(浄化装置の原理・設計やその運転管理、水質分析の原理・装置・方法など)の理解を深めることにある。詳しい数理学的な解析や手法は、それぞれの分野の専門書を参考とされたい。
ミクロ粒子の波動関数
波動力学では、ポテンシャル・エネルギーV(r)を知って、波動関数ψ(r)および固有エネルギー E を求めることとなる。粒子の波動関数に関するシュレーディンガー方程式はつぎのように表される。
((-ħ2/2m)∇2 + V(r))Ψ(r, t) = iħ(∂/∂t)Ψ(r, t) (H-1)
V(r) が時間的に変動しないとき、Ψ(r, t) = ψ(r)φ(t) とおいて、変数分離できるので、(H-1)から、定数(エネルギー) Eを用いて、つぎの2式が得られる。
iħ(∂/∂t)φ(t) = Eφ(t) (H-2)
( -(ħ2/2m)∇2 + V(r))ψ(r)= Eψ(r) (H-3)
(H-2)の解は、φ(t) = e-i(E/ħ)tとなり、E/ħ= 2πν = ωであるので、
Ψ(r, t) = ψ(r) e-iωt (H-4)
ψ(r)は粒子の空間分布に関する部分で、時間部分のφ(t)の角振動数ω(または振動数ν)は、E だけによってきまる。
(H-3)の解は、関数V(r)を指定することによって、求めることができる。V(r) = 0とすると、(ħ2/2m)∇2ψ(r)= -Eψ(r) となり、この一般解として、つぎのような E とψ(r)が得られる。
ψ(r) = C+eiκ・r + C–e-iκ・r (H-5)
E(κ) = (ħ2/2m)|κ|2 (H-6)
(H-5)と(H-6)が示す意味は、粒子m(質量)について、つぎのようにまとめることができる。
① r は空間における粒子の位置ベクトルで、3次元空間 r(x, y, z)では
ψ(x, y, z) = X(x)・Y(x)・Z(x) E = Ex + Ey + Ez
② κ は波数ベクトルと呼ばれ、3次元 κ 空間では κ(κx, κy, κz)となり、
κ2 = κx2 + κy2 + κz2
E(κ) = (ħ2/2m)(κx2 + κy2 + κz2)
③ eiκ・r は粒子が r 方向に、e-iκ・r は反対方向 –r へ進む物質波を表している。
④ 物質波の波長:λ= 2π/κ
⑤ 粒子の運動量:p = ħκ
⑥ r における粒子の存在確率:|ψ(r)|2 = ψ(r)* ψ(r)
⑦ 全空間で粒子を見出す確率:∫ψ(r)* ψ(r)d3r = 1(規格化)から、(H-5)式の係数C±が決定できる。
⑧ V(r) = 0 の条件下での粒子は自由粒子とよばれ、-∞~∞の全空間にわたって同じ確率で存在するので、空間のどこかに存在するが、それがどこなのか定まらない。
⑨ V(r) (≠ 0) とその境界条件のもとで、方程式(H-3)のψ(r)を求めると、粒子の存在確率が明確となる。有限な箱の中に粒子を閉じ込めると、箱の端の境界条件から係数 C±が決まり、E は離散的な値となる。
例えば、原子中の電子は、中心力が働く電界内の荷電粒子として、その波動関数ψn,l,m(r)とそのエネルギー En,l,mが求められる。
⑩ 巨視的な現象を、ミクロの視点から解析・説明するとき、空間ベクトルあるいはその成分を適宜、選択・変換して数学的取り扱いを行う。位置 r(x, y, x)、波数 κ(κx, κy, κz) ⇆ 運動量 p (px, py, pz)
<本ページの目的>
以下の各節で示す粒子の取扱いでは、上記の手順に沿って、様々な関数V(r)に対してその境界条件のもとで、固有関数ψ(r)とその固有値 E を求める。ψ(r)を求めるとき、V(r)によっては、数学的な工夫がなされる。
冒頭で述べたように、本ページの目的は、ψ(r)と E を数学的に求める方法ではなくて、解を求める条件とその結果(解)の意味を理解することにある。数学的な取扱いについては多数の著書(例えば、下記に記載の参考文献)やインターネット上に掲載されているので、興味のある方は参照されたい。
((-ħ2/2m)∇2 + V(r))Ψ(r, t) = iħ(∂/∂t)Ψ(r, t) (H-1)
V(r) が時間的に変動しないとき、Ψ(r, t) = ψ(r)φ(t) とおいて、変数分離できるので、(H-1)から、定数(エネルギー) Eを用いて、つぎの2式が得られる。
iħ(∂/∂t)φ(t) = Eφ(t) (H-2)
( -(ħ2/2m)∇2 + V(r))ψ(r)= Eψ(r) (H-3)
(H-2)の解は、φ(t) = e-i(E/ħ)tとなり、E/ħ= 2πν = ωであるので、
Ψ(r, t) = ψ(r) e-iωt (H-4)
ψ(r)は粒子の空間分布に関する部分で、時間部分のφ(t)の角振動数ω(または振動数ν)は、E だけによってきまる。
(H-3)の解は、関数V(r)を指定することによって、求めることができる。V(r) = 0とすると、(ħ2/2m)∇2ψ(r)= -Eψ(r) となり、この一般解として、つぎのような E とψ(r)が得られる。
ψ(r) = C+eiκ・r + C–e-iκ・r (H-5)
E(κ) = (ħ2/2m)|κ|2 (H-6)
(H-5)と(H-6)が示す意味は、粒子m(質量)について、つぎのようにまとめることができる。
① r は空間における粒子の位置ベクトルで、3次元空間 r(x, y, z)では
ψ(x, y, z) = X(x)・Y(x)・Z(x) E = Ex + Ey + Ez
② κ は波数ベクトルと呼ばれ、3次元 κ 空間では κ(κx, κy, κz)となり、
κ2 = κx2 + κy2 + κz2
E(κ) = (ħ2/2m)(κx2 + κy2 + κz2)
③ eiκ・r は粒子が r 方向に、e-iκ・r は反対方向 –r へ進む物質波を表している。
④ 物質波の波長:λ= 2π/κ
⑤ 粒子の運動量:p = ħκ
⑥ r における粒子の存在確率:|ψ(r)|2 = ψ(r)* ψ(r)
⑦ 全空間で粒子を見出す確率:∫ψ(r)* ψ(r)d3r = 1(規格化)から、(H-5)式の係数C±が決定できる。
⑧ V(r) = 0 の条件下での粒子は自由粒子とよばれ、-∞~∞の全空間にわたって同じ確率で存在するので、空間のどこかに存在するが、それがどこなのか定まらない。
⑨ V(r) (≠ 0) とその境界条件のもとで、方程式(H-3)のψ(r)を求めると、粒子の存在確率が明確となる。有限な箱の中に粒子を閉じ込めると、箱の端の境界条件から係数 C±が決まり、E は離散的な値となる。
例えば、原子中の電子は、中心力が働く電界内の荷電粒子として、その波動関数ψn,l,m(r)とそのエネルギー En,l,mが求められる。
⑩ 巨視的な現象を、ミクロの視点から解析・説明するとき、空間ベクトルあるいはその成分を適宜、選択・変換して数学的取り扱いを行う。位置 r(x, y, x)、波数 κ(κx, κy, κz) ⇆ 運動量 p (px, py, pz)
<本ページの目的>
以下の各節で示す粒子の取扱いでは、上記の手順に沿って、様々な関数V(r)に対してその境界条件のもとで、固有関数ψ(r)とその固有値 E を求める。ψ(r)を求めるとき、V(r)によっては、数学的な工夫がなされる。
冒頭で述べたように、本ページの目的は、ψ(r)と E を数学的に求める方法ではなくて、解を求める条件とその結果(解)の意味を理解することにある。数学的な取扱いについては多数の著書(例えば、下記に記載の参考文献)やインターネット上に掲載されているので、興味のある方は参照されたい。
よい量子数、結晶中電子の量子数、格子定数
(1)内核電子
原子核に拘束されている内核電子は、原子核がつくるクーロン場の中を運動するから。その運動を記述するのに極座標系 r(r, θ, ψ)が便利である。そして、その運動状態は主量子数 n(原子核からrにある球面波の量子化;n = 1, 2,・・・)、方位量子数 l(左記球面とxy平面との交線の円周波の量子化;l = 0, 1, 2,・・・, n-1)、磁気量子数m(z軸方向の波の量子化;0, ±1, ±2,・・・,±l) で示される量子数で指定される。
これにスピンの状態を指定するスピン量子数 s を加えた4つが‘よい量子数’として使われる。パウリの原理により量子数の組 (n, l, m, s)には2個以上の電子が入ることはできない。原子や分子中の電子の挙動を説明するときに用いられる。
これにスピンの状態を指定するスピン量子数 s を加えた4つが‘よい量子数’として使われる。パウリの原理により量子数の組 (n, l, m, s)には2個以上の電子が入ることはできない。原子や分子中の電子の挙動を説明するときに用いられる。
(2)結晶中の外殻電子
一方、結晶中を自由に運動する外殻電子(伝導電子)を扱うときには、直交座標系 r(x, y, z)を用いるほうが便利である。
伝導電子の量子状態に対しては、波数ベクトル κ(κx, κy, κz)が‘よい量子数’となる。当然、2個以上の電子が量子状態(κx, κy, κz, s)を占めることはできない。
今、電子が各辺(Lx, Ly, Lz)の直方体の箱に閉じ込められているとすると、波数ベクトルκは、ni (i=x, y, z) = 0, ±1, ±2,・・・を用いて、つぎのように量子化される。
κ = (nx(2π/Lx), ny(2π/Ly), nz(2π/Lz)) (C-1)
伝導電子の量子状態に対しては、波数ベクトル κ(κx, κ
今、電子が各辺(Lx, Ly, Lz)の直方体の箱に閉じ込められているとすると、波数ベクトルκは、ni (i=x, y, z) = 0, ±1, ±2,・・・を用いて、つぎのように量子化される。
κ = (nx(2π/Lx), ny(2π/Ly), nz(2π/Lz)) (C-1)
(3)結晶格子
以下の説明では混乱を避けるため、直交座標系(X, Y, Z)とし、この系での位置ベクトル r(rx, ry, rz)で示す。ここで、直方体 (a, b, c) の単位格子を考え、各頂点に原子が配置されているものとする。格子定数 (a, b, c) を単位格子ベクトルとし、整数 li (i=x, y, z) = 0, ±1, ±2,・・・を用いると、結晶内の各原子の位置ベクトル l (lxa, lyb, lzc) で示される。これに対して、整数 ni (i=x, y, z) = 0, ±1, ±2,・・・を用いて、ベクトルgを定義する。
g = (nx(2π/a),ny( 2π/b),nz(2π/c)) (C-2)
l を格子ベクトル、g を逆格子ベクトルという。gは式(C-1)で示す量子化された波数ベクトルκと同じ形のベクトルとなる。
g = (nx(2π/a),ny( 2π/b),nz(2π/c)) (C-2)
l を格子ベクトル、g を逆格子ベクトルという。gは式(C-1)で示す量子化された波数ベクトルκと同じ形のベクトルとなる。
<ミラー指数と結晶面>
ところで、ミラー指数 (hkl)を用い、X軸、Y軸、Z軸と交わる点(N/h, 0, 0)、(0, N/k, 0)、(0, 0, N/l)とする結晶面群 N(= 0,±1,±2,・・・)は次式で示される。
hX + kY + lZ = N (C-3)
平面(C-3)の法線ベクトル n(h, k, l) に2πを乗じたベクトル g(2πh, 2πk, 2πl)をミラー指数で示される結晶面に対する逆格子ベクトルという。
<注意> ミラー指数 (hkl)は、( )内をコンマ’,’で区切らないことに注意したい。
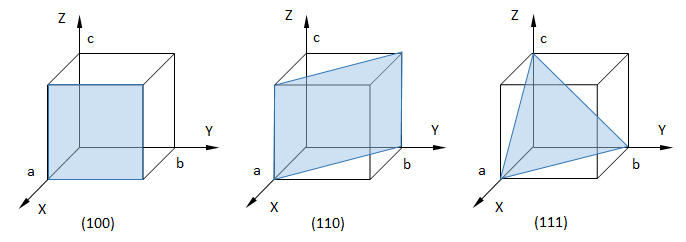
図C1 斜方晶(長方体型)の結晶単位格子と結晶面 (100)、(010)、(001)
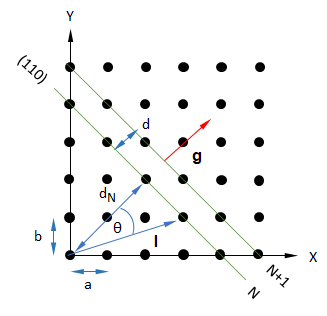
図C2 結晶面群 (110) と各結晶格子ベクトルの関係
結晶面群 (110) はディスプレイ面に垂直なZ軸方向に平行であり、図はXY平面での切口を示している。
目次へ
井戸型ポテンシャル
ポテンシャル(壁)で囲まれたミクロ(素)粒子の束縛状態を考える。現実的には3次元で取り扱うものであるが、1次元の取扱いが簡単で、これで現実の問題を説明できることが多い。
ポテンシャルの内側と外側の一般解を求め、両者の境界での接続条件を課す。エネルギーの固有値は解析的に求めることはできないが、作図によって解くことができる。井戸型ポテンシャルの取扱いは大学で履修する量子力学の参考書や一般の書籍に詳しく記載されているので、ここでは、その概要と結果について説明する。
図W1に示すようなエネルギーの壁があって、深さ Vo(>0)、幅 Lの矩形型井戸を考える。ただし、ミクロ粒子のエネルギーを E とし、0 > E ≧ -Vo とする。
V(x) = -Vo (|x| ≦ L) and 0 (|x| > L) (W-1)
このような井戸内に束縛された素粒子の固有関数をψ(x)とする。境界条件は、① ψ(x)→0 (|x|→∞) となること、② x = ±L で飛び値をもつが、ψ(x)は滑らかに連続していること。また、③エネルギー演算子ハミルトニアンH(x)は空間反転に対して不変であるので、H(-x) = H(x)となること(H:下式W-2の左辺の( )内で示される演算子)。
以上のような条件で、上記の時間に依存しないシュレーディンガー方程式(H-3)のψ(r)を、1次元の波動関数ψ(x)とし、その解を求める。
( -(ħ2/2m)∂2ψ/∂x2 + V(x))ψ(x) = Eψ(x) (W-2)
詳しい解法は省略して、上式の解は次式のようになる。
ψ(x) = ① C exp(κx) for x<-L、
② A coskx + B sinkx for -L≦x≦L、
③ D exp(-κx) for L<x
ħκ = √(-2mE)、 ħk = √(2m(E + Vo) (W-3)
係数 A~D は、上記の境界条件を適用して決定できるが、ここでは省略する。なお、①と③は対称なので、C = D となる。後述する自然数、n=0, 1, 2, 3,・・・、において、nが偶数のとき B = 0、奇数のとき A = 0となる。
一方、1次元シュレーディンガー方程式(W-2)のエネルギー固有値 En およびその固有関数 ψn(x) は解析(数学)的に解くことは困難であるが、図を描いて求めることができる(詳細な説明は省略するが、次式の範囲内に固有値 En がある)。なお、Vo → ∞ のとき、≦ → = となる。
n2π2ħ2/(8mL2) < Vo + En ≦ (n+1)2π2ħ2/(8mL2) (W-3)
自然数、n = 0, 1, 2,・・・, n、に対して、n+1個のエネルギー固有値 Enが得られる。なお、Vo + En は井戸の底からの距離(エネルギー差)を示し、井戸の上端からの距離 Vo – (Vo + En) = -En (>0) を束縛エネルギーという。
図W1(A)に各 En に対応する固有関数 ψn(n = 0, 1, 2 について)を示す(各関数を同じ位置に重ねて描くと煩雑となるので、対応するエネルギー固有値 En の高さに合わせて示してある。)。
なお、n が奇数(1, 3,・・・)に対応する固有関数は、ψ(x) = -ψ(-x)となっているが、特に気にすることではない。時間を含む固有関数は、ψ(x,t) = ψ(x) exp(-iωt)、ω= E/ħ、で示され、図中点線を含む複素平面がこの軸を中心に角速度ωで回転しているイメージである(n=1について、回転の様子を示している)。位相は変化しているが、存在確率を示す|ψ|2は同じ値となる。
<井戸型ポテンシャルの意味>
井戸に束縛された素粒子の存在確率は、図W2で示される。質点の古典力学ではあり得ないことであるが、ミクロの世界では、井戸の外側に素粒子の存在確率が広がっているこである。
x>L または x<-Lでは、exp(-κx) または exp(κx)で示される形で減衰しているが、(B)と(C)に示すように、κ の値が小さいほど、すなわち、粒子の質量m が小さいほど、ポテンシャル Vo が低い(井戸の深さが浅い)ほど、また、粒子の束縛エネルギー -E が小さいほど、井戸外での確率分布の広がりが大きくなる。
(A)に示すように「無限に深い井戸型ポテンシャル、Vo → ∞」では、原子核の強力な核力に捕らえられた陽子や中性子などの振る舞いを雑把に説明できる。この場合、素粒子が井戸の外側に存在する確率、∫ψ*(x)ψ(x) dx (L<|x|<∞)→ 0、となり、井戸の外での存在確率は無限小となる。
ポテンシャルの内側と外側の一般解を求め、両者の境界での接続条件を課す。エネルギーの固有値は解析的に求めることはできないが、作図によって解くことができる。井戸型ポテンシャルの取扱いは大学で履修する量子力学の参考書や一般の書籍に詳しく記載されているので、ここでは、その概要と結果について説明する。
図W1に示すようなエネルギーの壁があって、深さ Vo(>0)、幅 Lの矩形型井戸を考える。ただし、ミクロ粒子のエネルギーを E とし、0 > E ≧ -Vo とする。
V(x) = -Vo (|x| ≦ L) and 0 (|x| > L) (W-1)
このような井戸内に束縛された素粒子の固有関数をψ(x)とする。境界条件は、① ψ(x)→0 (|x|→∞) となること、② x = ±L で飛び値をもつが、ψ(x)は滑らかに連続していること。また、③エネルギー演算子ハミルトニアンH(x)は空間反転に対して不変であるので、H(-x) = H(x)となること(H:下式W-2の左辺の( )内で示される演算子)。
以上のような条件で、上記の時間に依存しないシュレーディンガー方程式(H-3)のψ(r)を、1次元の波動関数ψ(x)とし、その解を求める。
( -(ħ2/2m)∂2ψ/∂x2 + V(x))ψ(x) = Eψ(x) (W-2)
詳しい解法は省略して、上式の解は次式のようになる。
ψ(x) = ① C exp(κx) for x<-L、
② A coskx + B sinkx for -L≦x≦L、
③ D exp(-κx) for L<x
ħκ = √(-2mE)、 ħk = √(2m(E + Vo) (W-3)
係数 A~D は、上記の境界条件を適用して決定できるが、ここでは省略する。なお、①と③は対称なので、C = D となる。後述する自然数、n=0, 1, 2, 3,・・・、において、nが偶数のとき B = 0、奇数のとき A = 0となる。
一方、1次元シュレーディンガー方程式(W-2)のエネルギー固有値 En およびその固有関数 ψn(x) は解析(数学)的に解くことは困難であるが、図を描いて求めることができる(詳細な説明は省略するが、次式の範囲内に固有値 En がある)。なお、Vo → ∞ のとき、≦ → = となる。
n2π2ħ2/(8mL2) < Vo + En ≦ (n+1)2π2ħ2/(8mL2) (W-3)
自然数、n = 0, 1, 2,・・・, n、に対して、n+1個のエネルギー固有値 Enが得られる。なお、Vo + En は井戸の底からの距離(エネルギー差)を示し、井戸の上端からの距離 Vo – (Vo + En) = -En (>0) を束縛エネルギーという。
図W1(A)に各 En に対応する固有関数 ψn(n = 0, 1, 2 について)を示す(各関数を同じ位置に重ねて描くと煩雑となるので、対応するエネルギー固有値 En の高さに合わせて示してある。)。
なお、n が奇数(1, 3,・・・)に対応する固有関数は、ψ(x) = -ψ(-x)となっているが、特に気にすることではない。時間を含む固有関数は、ψ(x,t) = ψ(x) exp(-iωt)、ω= E/ħ、で示され、図中点線を含む複素平面がこの軸を中心に角速度ωで回転しているイメージである(n=1について、回転の様子を示している)。位相は変化しているが、存在確率を示す|ψ|2は同じ値となる。
<井戸型ポテンシャルの意味>
井戸に束縛された素粒子の存在確率は、図W2で示される。質点の古典力学ではあり得ないことであるが、ミクロの世界では、井戸の外側に素粒子の存在確率が広がっているこである。
x>L または x<-Lでは、exp(-κx) または exp(κx)で示される形で減衰しているが、(B)と(C)に示すように、κ の値が小さいほど、すなわち、粒子の質量m が小さいほど、ポテンシャル Vo が低い(井戸の深さが浅い)ほど、また、粒子の束縛エネルギー -E が小さいほど、井戸外での確率分布の広がりが大きくなる。
(A)に示すように「無限に深い井戸型ポテンシャル、Vo → ∞」では、原子核の強力な核力に捕らえられた陽子や中性子などの振る舞いを雑把に説明できる。この場合、素粒子が井戸の外側に存在する確率、∫ψ*(x)ψ(x) dx (L<|x|<∞)→ 0、となり、井戸の外での存在確率は無限小となる。
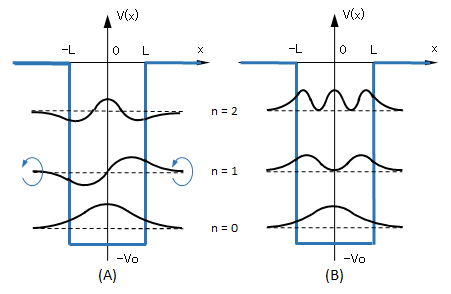
図W1 井戸型ポテンシャル内のミクロ粒子 (A) 固有関数 φn(x)、(B) 確率分布 |φn(x)|2
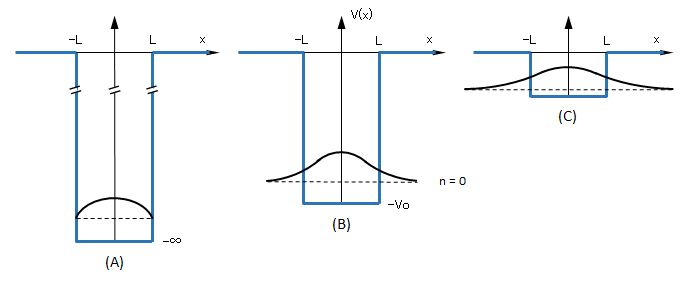
図W2 井戸型ポテンシャルの深さと固有関数φn(x)、 (n=0)、の広がり
深さ(束縛エネルギー Vo):(A) 無限大、(B) 深い(大きい)、(C) 浅い(小さい)
目次へ
トンネル効果
古典的力学においては、エネルギーEをもつ質点が、進行方向にある高さ(エネルギー)Vo(E<Vo)の壁を越えて行くことはなく、跳ね返され反対方向へ進行する。しかし、ミクロ粒子の世界では、条件によっては、この壁を越えて進行することが可能で、これはトンネル効果といわれる。壁を越えて進行できる確率を透過率 T (0<T<1) という。ここでは、T についての解析事例の一つを紹介する。
今、図T1にしめすように、ミクロ粒子が左から右に向かって進行し、壁に当たった状況を考える。ただし、0 < E ≦ -Voとする。
x<0 : ψ(x) = Aeikx + Be-ikx ħk = √(2m(Vo + E) (T-1)
0≦x≦L: ψ(x) = Feiκx + Ge-iκx ħκ= √(-2mE) (T-2)
x>L : ψ(x) = Ceikx ħk = √(2m(Vo + E) (T-3)
Aeikxは進行波で、Be-kxは壁による反射波である。
井戸型ポテンシャルの境界条件②で述べたように、上記領域の関数 ψ(x) が滑らかに連続する条件(領域の境界における x 値において、それぞれの領域のψ(x) および dψ(x)/dx の値が等しくなること)を適用すると、次の関係式が得られる。
x = 0 において、
A +B = F+G、 ikA – ikB = κF – κG
X = Lにおいて、
FeκL + Ge-κL = CeikL、 κFeκL – κGe-κL = ikCeikL、
井戸型ポテンシャルで示した境界条件①、②の下で、上記の連立方程式を解き、係数A~Gの値を決定することができる。ここで、x<0 および x>L における粒子の移動速度は同じなので、係数の絶対値の2乗の比を計算すれば、それが透過率Tを表すこととなる。
T = |C|2/|A|2
= 4(kκ)2/(4(kκ)2(k2 + κ2)2sinh2(κL) )
≒ 16(kκ)2/(k2 + κ2)2・e-2κL (T-4)
|A|2 = |B|2 + |C|2
なお、上式のκL = 2π(L/λ)で示される。
<トンネル効果の意味>
透過率Tで注目すべき事項は、指数関数部分で、壁の厚さ L が大きいほど、すなわち、厚さ L が物質波の波長λより大きくなった辺りから、トンネル効果が急激に減少することである。
トンネル効果は、半導体素子、放射性物質からのα粒子の放出、電極-溶液界面での電子の移動など、様々な現象を説明できる。
今、図T1にしめすように、ミクロ粒子が左から右に向かって進行し、壁に当たった状況を考える。ただし、0 < E ≦ -Voとする。
x<0 : ψ(x) = Aeikx + Be-ikx ħk = √(2m(Vo + E) (T-1)
0≦x≦L: ψ(x) = Feiκx + Ge-iκx ħκ= √(-2mE) (T-2)
x>L : ψ(x) = Ceikx ħk = √(2m(Vo + E) (T-3)
Aeikxは進行波で、Be-kxは壁による反射波である。
井戸型ポテンシャルの境界条件②で述べたように、上記領域の関数 ψ(x) が滑らかに連続する条件(領域の境界における x 値において、それぞれの領域のψ(x) および dψ(x)/dx の値が等しくなること)を適用すると、次の関係式が得られる。
x = 0 において、
A +B = F+G、 ikA – ikB = κF – κG
X = Lにおいて、
FeκL + Ge-κL = CeikL、 κFeκL – κGe-κL = ikCeikL、
井戸型ポテンシャルで示した境界条件①、②の下で、上記の連立方程式を解き、係数A~Gの値を決定することができる。ここで、x<0 および x>L における粒子の移動速度は同じなので、係数の絶対値の2乗の比を計算すれば、それが透過率Tを表すこととなる。
T = |C|2/|A|2
= 4(kκ)2/(4(kκ)2(k2 + κ2)2sinh2(κL) )
≒ 16(kκ)2/(k2 + κ2)2・e-2κL (T-4)
|A|2 = |B|2 + |C|2
なお、上式のκL = 2π(L/λ)で示される。
<トンネル効果の意味>
透過率Tで注目すべき事項は、指数関数部分で、壁の厚さ L が大きいほど、すなわち、厚さ L が物質波の波長λより大きくなった辺りから、トンネル効果が急激に減少することである。
トンネル効果は、半導体素子、放射性物質からのα粒子の放出、電極-溶液界面での電子の移動など、様々な現象を説明できる。
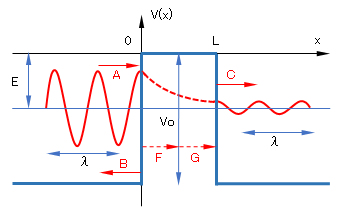
図T1 エネルギーの壁とトンネル効果
Vo-障壁の高さ(エネルギー)、L-障壁の厚さ、E-粒子のエネルギー
式(T-1)〜(T-3)で示す物質波:A-進行波、B-反射波、C-透過波、F・G-減衰波
目次へ
調和振動子とポテンシャル曲線
中心から力を受けている粒子の挙動は、理想的なバネに繋がれて振動している物体の運動(調和振動)で近似的に説明されることが多い。このような系は調和振動子と呼ばれ、ここでは1次元のみの単純な系について概説する[詳しくは、Pitzer, 1963; 弘江, 2015、などを参照]。調和振動は変位に比例した復元力が働くときに起こる。
F = -kx → F(x) = -dV(x)/dx →
V(x) = kx2/2 (O-1)
バネに繋がれている振動する質量mの質点の運動は、
x = Acos(ωt + θ) (ω = √(k/ω) →
k = mω2 (O-2)
(O-2)式を(O-1)式に代入すると、
V(x) = mω2x2/2 (O-3)
上記(H-3)式のψ(r)を1次元の波動関数ψ(x)として扱い、これに(O-3)式を代入すると、次式が得られる。
(-(ħ2/2m)∂2/∂x2 + mω2x2/2)ψ(x) = Eψ(x)
ここで、ξ= √(mω/ħ)x、ε=2E/(ħω) とおいて、ψ(x) → φ(ξ)とすると、上式の解は次式で示される。
φ(ξ) = cHn(ξ)exp(-ξ2/2) (2)
Hn(ξ) = (-1)nexp(ξ2)dn/dξn(exp(-ξ2/2)) (エルミート多項式)
上式のcは任意の定数で許されるが、粒子の存在確率が全体で’1’になるようにすれば決定される。
一方、エネルギーは、離散的な値をとり、hν = ħωであるので、次式で示される。
E = hν(n + 1/2) (n = 0, 1, 2,・・・)
波動関数φ(ξ)の絶対値を2乗したものは、粒子の存在確立を表し、これをグラフ化したものが図H1である。ただし、φ(ξ)をψ(x)に変換したものについて、図示してある。存在確率の曲線を同じ位置に重ねて描くと煩雑になるので、量子数nで示されるエネルギーの高さに合わせて示してある。
<調和振動子の意味>
図H1から、2つの重要な事項が理解できる。
(1)古典力学では、エネルギーの高さを示す2次曲線が切り抜く範囲までしか質点は移動できない。これは、放物線で示す位置で運動エネルギーがゼロになり、放物線の範囲内で質点は単振動する。一方、量子力学的な確率の波は、放物線で示す範囲を越えて広がっている。ただし、この範囲を越えると存在確率は急激に減衰しているが、理論上は無限遠に至るまで0ではない。
(2)古典力学の単振動では、質点の見出される確率は、x=0 で最小(速度が最大)で、放物線上で最大(速度が0)であるのに対して、量子力学での粒子の確率分布は、放物線内に極大値が(n+1)点で見出されることである。
F = -kx → F(x) = -dV(x)/dx →
V(x) = kx2/2 (O-1)
バネに繋がれている振動する質量mの質点の運動は、
x = Acos(ωt + θ) (ω = √(k/ω) →
k = mω2 (O-2)
(O-2)式を(O-1)式に代入すると、
V(x) = mω2x2/2 (O-3)
上記(H-3)式のψ(r)を1次元の波動関数ψ(x)として扱い、これに(O-3)式を代入すると、次式が得られる。
(-(ħ2/2m)∂2/∂x2 + mω2x2/2)ψ(x) = Eψ(x)
ここで、ξ= √(mω/ħ)x、ε=2E/(ħω) とおいて、ψ(x) → φ(ξ)とすると、上式の解は次式で示される。
φ(ξ) = cHn(ξ)exp(-ξ2/2) (2)
Hn(ξ) = (-1)nexp(ξ2)dn/dξn(exp(-ξ2/2)) (エルミート多項式)
上式のcは任意の定数で許されるが、粒子の存在確率が全体で’1’になるようにすれば決定される。
一方、エネルギーは、離散的な値をとり、hν = ħωであるので、次式で示される。
E = hν(n + 1/2) (n = 0, 1, 2,・・・)
波動関数φ(ξ)の絶対値を2乗したものは、粒子の存在確立を表し、これをグラフ化したものが図H1である。ただし、φ(ξ)をψ(x)に変換したものについて、図示してある。存在確率の曲線を同じ位置に重ねて描くと煩雑になるので、量子数nで示されるエネルギーの高さに合わせて示してある。
<調和振動子の意味>
図H1から、2つの重要な事項が理解できる。
(1)古典力学では、エネルギーの高さを示す2次曲線が切り抜く範囲までしか質点は移動できない。これは、放物線で示す位置で運動エネルギーがゼロになり、放物線の範囲内で質点は単振動する。一方、量子力学的な確率の波は、放物線で示す範囲を越えて広がっている。ただし、この範囲を越えると存在確率は急激に減衰しているが、理論上は無限遠に至るまで0ではない。
(2)古典力学の単振動では、質点の見出される確率は、x=0 で最小(速度が最大)で、放物線上で最大(速度が0)であるのに対して、量子力学での粒子の確率分布は、放物線内に極大値が(n+1)点で見出されることである。
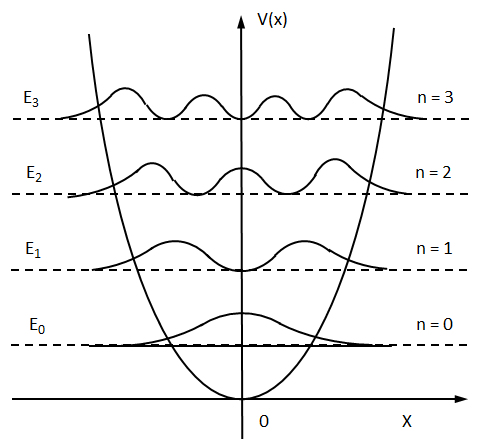
図H1 調和振動子のエネルギーと確率分布
目次へ
ミクロ粒子の統計力学
熱力学は、第1~第3法則に基づき熱平衡にある系の性質について考える。このとき、経験法則を抽象化し、ミクロな構造に立ち入ることはない。たとえば気体を取り上げると、熱学量である圧力、体積、温度の関係式である状態方程式は、経験則であるボイル・シャルルの法則が基本となっている。一方、ミクロな構造にまで立ち入って体系の状態を表そうとするのが統計力学である。
我々の観測対象となる状態は、マクロに見ると一つの状態でも、ミクロに見ると非常に多くの粒子からなっている。これらを統計的に扱うことで、体系の観測される性質を理論的に導こうするのが統計力学である。編集者にとって統計力学は専門外であるので、ここでは定義と結論のみに止めており、詳細は専門書を参考としてもらいたい。
我々の観測対象となる状態は、マクロに見ると一つの状態でも、ミクロに見ると非常に多くの粒子からなっている。これらを統計的に扱うことで、体系の観測される性質を理論的に導こうするのが統計力学である。編集者にとって統計力学は専門外であるので、ここでは定義と結論のみに止めており、詳細は専門書を参考としてもらいたい。
1.統計集団
ある状態にある多数の粒子(分子、原子、電子など)を一つの体系の集合体と考え、この体系の集合体で着目している系を分析する。この体系の集合体のことを統計集団(ensemble)という。このような統計集団には、小正準集団(micro-canonical ensemble)、正準集団(canonical ensemble)、大正準集団(grand-canonical ensemble)と呼ばれる3つの集団がある。
(1)小正準集団
粒子数 N、体積 V、エネルギー E が一定条件の下で平衡状態にある体系がとりうるすべての微視的状態が、等しい確率で出現している統計集団をいう。古典力学に基づく表現を用いれば、この系にあるすべての粒子の力学量X(q, p)、(粒子の位置q、運動量p)、の位相空間分布として、出現確率ρは、つぎのようになる。外界から孤立した体系の平衡状態を取り扱うのに適している。
① X(q, p)が等エネルギー面HN(q, p) = E にあるとき、
ρ(q, p) = 一定 ≠ 0
② ①以外のとき
ρ(q, p) = 0
なお、
HN(q, p) = Σpi2/(2mi) + Φ(q1, q2,・・・, qN) (ハミルトニアン関数)
① X(q, p)が等エネルギー面HN(q, p) = E にあるとき、
ρ(q, p) = 一定 ≠ 0
② ①以外のとき
ρ(q, p) = 0
なお、
HN(q, p) = Σpi2/(2mi) + Φ(q1, q2,・・・, qN) (ハミルトニアン関数)
(2)正準集団
粒子数 N、体積 V、温度 Tが指定された体系に許される微視的状態のうちで、エネルギー E に等しいものの出現確率がつぎのように用意されたものを正準集合という。外界とのエネルギー交換が許される体系を取り扱うのに適している。
ρ(E) = e-E/kT/Σe-E/kT
古典力学での表現を用いれば、位相空間分布はつぎのようになる。
ρ(q, p) = exp(-HN(q, p)/kT)/∫exp(-HN(q, p))dqdp
ρ(E) = e-E/kT/Σe-E/kT
古典力学での表現を用いれば、位相空間分布はつぎのようになる。
ρ(q, p) = exp(-HN(q, p)/kT)/∫exp(-HN(q, p))dqdp
(3)大正準集団
粒子数 N、体積 V、化学ポテンシャル μ が一定に指定された体系に許される微視的状態のうちで、エネルギー E に等しく、粒子数が N に等しいものの出現確率が、つぎのように与えられるものを正準集合という。体系への粒子の出入が自由である体系を取り扱うのに適している。
ρ(N, E) = e(μN – E)/kT/ΣΣ e(μN – E)
ρ(N, E) = e(μN – E)/kT/ΣΣ e(μN – E)
2.量子統計
量子力学の世界では、体系のもつエネルギーが連続的でなく、離散的な値をとる。体系がとりうるエネルギー準位を考慮し、統計力学として扱うことで、ボーズ・アインシュタイン統計、フェルミ・ディラック統計が説明される。ここでは、大正準集団のみの量子統計について説明する。
(1)ボーズ粒子とフェルミ粒子
量子力学によると、あるエネルギー準位に対して、粒子の準位の取り方が2種類ある。
① 1つの準位に対して、何個でも入ることが可能な粒子
② 1つの準位に対して、1個しか入ること許される粒子
①はボーズ粒子といわれ、光子、音子、振動子などがある。②はフェルミ粒子とよばれ、電子、中性子、陽子などがあげられる。1個の粒子が1つの準位にあり、他の粒子が入ることができないことを、パウリの排他律という。
フェルミ粒子が奇数個結合したものは、フェルミ・ディラック統計にしたがい、偶数個が結合したものはボーズ・アイシュタイン統計にしたがう。たとえば、3He原子(陽子2つ、中性子1つ、電子2つ)はフェルミ粒子、4He(陽子2つ、中性子2つ、電子2つ)はボーズ粒子である。
① 1つの準位に対して、何個でも入ることが可能な粒子
② 1つの準位に対して、1個しか入ること許される粒子
①はボーズ粒子といわれ、光子、音子、振動子などがある。②はフェルミ粒子とよばれ、電子、中性子、陽子などがあげられる。1個の粒子が1つの準位にあり、他の粒子が入ることができないことを、パウリの排他律という。
フェルミ粒子が奇数個結合したものは、フェルミ・ディラック統計にしたがい、偶数個が結合したものはボーズ・アイシュタイン統計にしたがう。たとえば、3He原子(陽子2つ、中性子1つ、電子2つ)はフェルミ粒子、4He(陽子2つ、中性子2つ、電子2つ)はボーズ粒子である。
(2)エネルギー分布
量子統計での大正準統計集団において、エネルギーεjを有する粒子の分布関数はつぎのようになる。
f(εj) = 1/(eβ(εj – μ) ± 1) (S-1)
ただし、β = 1/kT
上式の(±)において、(+)はフェルミ粒子、(-)はボーズ粒子に対応する。β(εj – μ) ≫ 1のとき、すなわち、温度 T が十分高く、粒子密度 N/V が小さい場合(希薄な気体など)には、つぎのマクスウェル・ボルツマン統計の式で近似される。
f(εj) = e-β(εj – μ) (S-2)
なお、集団の全粒子数 N、全エネルギー E とし、エネルギー準位 εj を nj個の粒子が占めるものとすると、分布関数 nj = f(εj)には、つぎの関係がある。
ε0<ε1<ε2<、・・・、<εN-1<、・・・
∑nj = N、 ∑njεj = E
∑f(εj) = N、 ∑εjf(εj) = E (S-3)
f(εj) = 1/(eβ(εj – μ) ± 1) (S-1)
ただし、β = 1/kT
上式の(±)において、(+)はフェルミ粒子、(-)はボーズ粒子に対応する。β(εj – μ) ≫ 1のとき、すなわち、温度 T が十分高く、粒子密度 N/V が小さい場合(希薄な気体など)には、つぎのマクスウェル・ボルツマン統計の式で近似される。
f(εj) = e-β(εj – μ) (S-2)
なお、集団の全粒子数 N、全エネルギー E とし、エネルギー準位 εj を nj個の粒子が占めるものとすると、分布関数 nj = f(εj)には、つぎの関係がある。
ε0<ε1<ε2<、・・・、<εN-1<、・・・
∑nj = N、 ∑njεj = E
∑f(εj) = N、 ∑εjf(εj) = E (S-3)
<量子統計の意味>
上式(S-1)、(S-2)において、β(εj – μ) = βμ(εj/μ – 1) とし、N は極めて大きな数値である。εj は離散的な値であるが、ε を連続的な値として、f(ε) を ε/μ に対してプロットしたものを図S1に示す。温度 T と f(ε) との関係を示すため、kT を μ に対する比率 r(kT = rμ)を変えて図示した(図中の①~⑥)。r → 0 のとき、T → 0 となる。
この図からボーズ粒子とフェルミ粒子の特徴が理解できる。T → 0 となると、ボーズ粒子では、ε/μ = 1 (ε = μ)において f(εj) → N となる。ボーズ粒子は、1つの準位に何個でも入ることができるので、T → 0 において、最低のエネルギー準位 ε0 にすべての粒子が入ることを示している。
一方で、T → 0 において、フェルミ粒子では、1つのエネルギー準位 εj に1個しか入れないので、上の準位にどんどん入っていくが、エネルギー準位 εN-1(εN-1<μ<εN・・・(S-4))のところまでで、存在する N 個の粒子が全ておさまってしまえば、それ以上のエネルギー準位(εj > μ)は空であることを示している。フェルミ分布関数において、μ をフェルミ準位またはフェルミポテンシャルということが多い。
上記のように、T → 0 においては、集団を構成する全粒子が、エネルギー準位 εj(≦ μ、’=’ はボーズ粒子のみ)を占めており、この現象を縮退しているという。フェルミ分布では、たとえば、図S1(C)-③に見られるように、フェルミ分布では、T → 0 でなくても、ε/μ ≦ c のa領域において、f(ε) = 1 となっており、縮退が起こっている。集団の粒子数N、体積Vが一定であるならば、μ(T)は温度低下とともに増加するので、ある温度Tc以下では縮退現象が生じることとなる。なお、b領域の現象を非縮退という。
なお、電子の集団を理想フェルミ粒子の模型として扱うが、電子は内部自由度として±1/2のスピンをもつ。電子は電荷をもっているので、並進運動とスピンは相互に影響しあうが、外部磁場がない場合には、その相互作用のエネルギーは小さいので無視されることが多い。電子の運動エネルギー (ħ/2m)/k2、k = |k|とすると、1つのk準位に2つの電子が入るという。
この図からボーズ粒子とフェルミ粒子の特徴が理解できる。T → 0 となると、ボーズ粒子では、ε/μ = 1 (ε = μ)において f(εj) → N となる。ボーズ粒子は、1つの準位に何個でも入ることができるので、T → 0 において、最低のエネルギー準位 ε0 にすべての粒子が入ることを示している。
一方で、T → 0 において、フェルミ粒子では、1つのエネルギー準位 εj に1個しか入れないので、上の準位にどんどん入っていくが、エネルギー準位 εN-1(εN-1<μ<εN・・・(S-4))のところまでで、存在する N 個の粒子が全ておさまってしまえば、それ以上のエネルギー準位(εj > μ)は空であることを示している。フェルミ分布関数において、μ をフェルミ準位またはフェルミポテンシャルということが多い。
上記のように、T → 0 においては、集団を構成する全粒子が、エネルギー準位 εj(≦ μ、’=’ はボーズ粒子のみ)を占めており、この現象を縮退しているという。フェルミ分布では、たとえば、図S1(C)-③に見られるように、フェルミ分布では、T → 0 でなくても、ε/μ ≦ c のa領域において、f(ε) = 1 となっており、縮退が起こっている。集団の粒子数N、体積Vが一定であるならば、μ(T)は温度低下とともに増加するので、ある温度Tc以下では縮退現象が生じることとなる。なお、b領域の現象を非縮退という。
なお、電子の集団を理想フェルミ粒子の模型として扱うが、電子は内部自由度として±1/2のスピンをもつ。電子は電荷をもっているので、並進運動とスピンは相互に影響しあうが、外部磁場がない場合には、その相互作用のエネルギーは小さいので無視されることが多い。電子の運動エネルギー (ħ/2m)/k2、k = |k|とすると、1つのk準位に2つの電子が入るという。
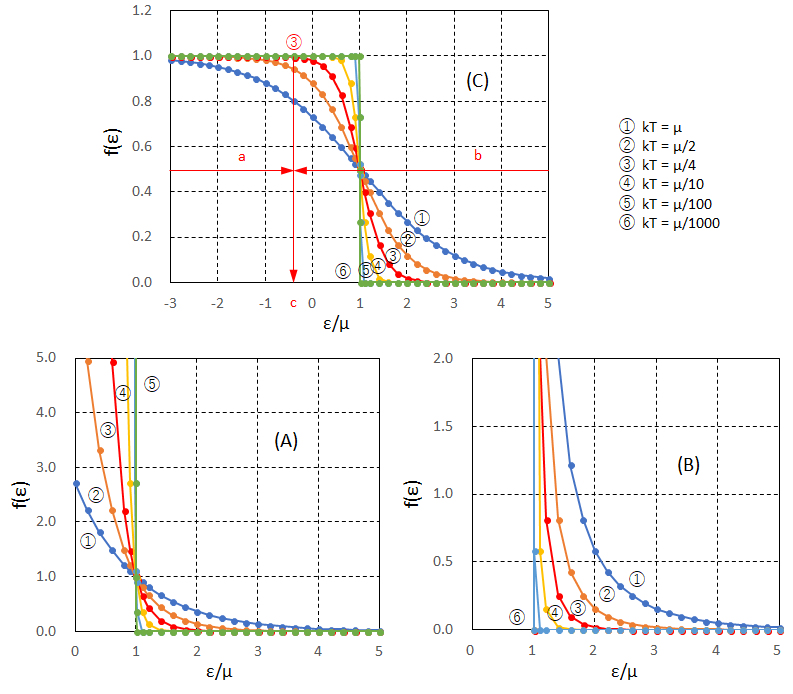
図S1 ミクロ粒子のエネルギー分布関数と温度
(A)ボルツマン分布、(B)ボーズ分布、(C)フェルミ分布
目次へ
光子エネルギーと粒子測定
光子(電磁波)は、電子・原子核・原子・分子などの物質の状態・量の測定に多用される。光子のエネルギー ε は次式で示される。
ε = hν、 ν = c/λ
ここで、プランク定数 h、光の速度 c、光子の波長 λ である。
表P1に光子のエネルギー・種類と測定対象を示す。例えば、原子の発光・吸収スペクトル、原子・分子の振動・回転の測定について、別ページに示す。
ε = hν、 ν = c/λ
ここで、プランク定数 h、光の速度 c、光子の波長 λ である。
表P1に光子のエネルギー・種類と測定対象を示す。例えば、原子の発光・吸収スペクトル、原子・分子の振動・回転の測定について、別ページに示す。
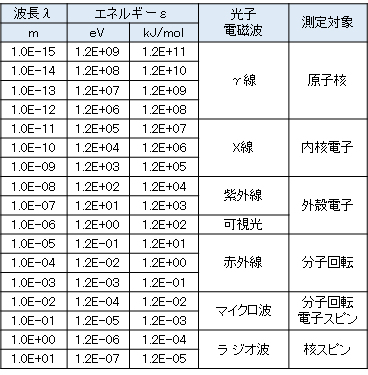
c = 2.9979 x 108 m/s、h = 6.6256 x 10-34 Js
目次へ
参考文献
E. Merzbacher, 1970: Quantum Mechanics, John Wiley & Sons.
K.S. Pitzer, 1963: Quantum Chemistry, Prentice-Hall.
C.A. Wert & R.M. Thomson, 1970: Physics of Solids, McGraw-Hill.
安達 健五 監修、1969: 金属の電子論 1、アグネ.
市村 浩、1968: 統計力学、裳華房.
久保 亮吾、1934: 統計力学、共立全書.
為近 和彦、2008: 熱・統計力学、北森出版.
沼居 貴陽、2007: 固体物性入門、森北出版.
広江 克彦、2015: 趣味で量子力学、理工図書.
水谷 宇一郎、1995: 金属電子論(上)、内田老鶴圃.
渡辺 正・中林誠一郎、1996: 電子移動の化学―電気化学入門、朝倉書店.
渡辺 正義・米屋 勝利、2002: 物質科学入門、化学同人.
掲載日:2018年5月26日
更新日:2018年6月21日
