村上定瞭(水浄化フォーラム)
物質(原子・分子)の安定性・反応性・移動性などの挙動や特徴を考えるとき、質点・球状剛体として扱うことも少なくないが、原子・分子は立体的な構造(弾性的)を有しているので、このことを理解していないと説明ができないことが多い。
原子(内部の電子構造)・分子構造(構成原子の立体的な配置)には、様々な静的・動的な状態・形態・形状があり、それらを説明するにあたり、多様な記号(表記法)が用いられる。その中の1つに対称性(symmetry)がある。これを数学的に扱う分野として、群論(group theory)がある。原子・分子を量子力学的に扱うとき、群論の理念が導入される。化学・物理法による物質の測定において、その原理や解析を群論(記号)で説明することは少なくない。結晶構造の扱いにおいても、同様である。水に係わる現象の解析と浄化プロセスの開発・設計において、対象となる物質の対称性は重要な示唆を与える。
群論(理念と記号)は対称性のある事象を説明する際に極めて効果的で説明を簡略化できるので、本サイト内でも多用している。しかし、数学的に扱うと抽象的で極めて分かりぬくい。化学分野で扱う対称性については、具体的な事例と関連づけて理解すること、または、慣れることが大切と考えている。化学群論を理解することで、量子力学や応用数学での群論が理解しやすくなる。
原子(内部の電子構造)・分子構造(構成原子の立体的な配置)には、様々な静的・動的な状態・形態・形状があり、それらを説明するにあたり、多様な記号(表記法)が用いられる。その中の1つに対称性(symmetry)がある。これを数学的に扱う分野として、群論(group theory)がある。原子・分子を量子力学的に扱うとき、群論の理念が導入される。化学・物理法による物質の測定において、その原理や解析を群論(記号)で説明することは少なくない。結晶構造の扱いにおいても、同様である。水に係わる現象の解析と浄化プロセスの開発・設計において、対象となる物質の対称性は重要な示唆を与える。
群論(理念と記号)は対称性のある事象を説明する際に極めて効果的で説明を簡略化できるので、本サイト内でも多用している。しかし、数学的に扱うと抽象的で極めて分かりぬくい。化学分野で扱う対称性については、具体的な事例と関連づけて理解すること、または、慣れることが大切と考えている。化学群論を理解することで、量子力学や応用数学での群論が理解しやすくなる。
1.対称操作と対称要素
対称要素
軸の周りに回したり、面に対して射影したりする操作を対称操作 (symmery operation) という。この操作に関わる軸 (axis)、面 (plane)、あるいは、点 (point)などを対称要素 (symmetry element) とよぶ。以下に述べる対称操作は、対称要素に基づいて行われる 1つあるいは複数の操作に対応している。対称要素と対称操作は密接に関係しており、本サイトでは、煩雑さを避けるために、「対称要素」と「対称操作」という用語は、あえて区別しないで用いることにする。
対称操作
次に示す 5 つのクラス(class)の対称操作がある。
(1) Cn :分子を貫く軸に対して 2π/n の角度だけ回転する操作 (proper rotaion、狭義の回転)
この対称要素は Cn (n 回転) と表記され、この操作を、n 回繰り返すと「もと」と完全に一致する。
(2) σ:分子を横切る平面に対して写像を作る操作 (reflection)
この対称要素は σ で表され、σh は主軸に垂直な対称面を、σv は主軸を含む対称面を表す。他に σd 面があるが、後述する。
(3) i :分子内の点に対して全ての原子を写映(反転)する操作 (inversion)
この対称要素並びに対応する操作を i という記号で表す。
(4) Sn :Cn 軸の周りに回転してから、Cn 軸と直交する対称面 σh に対して写像を作る。あるいは、その逆に Cn 軸と直交する対称面 σh に対して写像を作ったのちに、それを Cn 軸の周りに回転する操作 (improper rotation)
次式のように、それぞれの操作は、対称要素を用いて表記し、その積で操作の順番を表す。後ろに書いた方の記号の操作を先に行う約束である。
Cn ✕ σ = σ ✕ Cn
この操作を回映・回反・広義の回転(improper rotation)という。このような対称要素は Sn で表し、この操作を Sn 操作と称する。擬回転(pseudo rotation)とは異なり、擬回転については、他ページで説明する。
(5)E :何もしないという操作
これを恒等変換とよび、その要素と操作は E という記号で表す。
(1) Cn :分子を貫く軸に対して 2π/n の角度だけ回転する操作 (proper rotaion、狭義の回転)
この対称要素は Cn (n 回転) と表記され、この操作を、n 回繰り返すと「もと」と完全に一致する。
(2) σ:分子を横切る平面に対して写像を作る操作 (reflection)
この対称要素は σ で表され、σh は主軸に垂直な対称面を、σv は主軸を含む対称面を表す。他に σd 面があるが、後述する。
(3) i :分子内の点に対して全ての原子を写映(反転)する操作 (inversion)
この対称要素並びに対応する操作を i という記号で表す。
(4) Sn :Cn 軸の周りに回転してから、Cn 軸と直交する対称面 σh に対して写像を作る。あるいは、その逆に Cn 軸と直交する対称面 σh に対して写像を作ったのちに、それを Cn 軸の周りに回転する操作 (improper rotation)
次式のように、それぞれの操作は、対称要素を用いて表記し、その積で操作の順番を表す。後ろに書いた方の記号の操作を先に行う約束である。
Cn ✕ σ = σ ✕ Cn
この操作を回映・回反・広義の回転(improper rotation)という。このような対称要素は Sn で表し、この操作を Sn 操作と称する。擬回転(pseudo rotation)とは異なり、擬回転については、他ページで説明する。
(5)E :何もしないという操作
これを恒等変換とよび、その要素と操作は E という記号で表す。
2.点群の表記とその例
様々な点群があるが、化学構造に関わりの深い代表的な分子例を挙げて、点群表記を説明する。以下の例に示すように、n が最も大きい回転軸を主軸として識別する。各点群を代表する分子と一緒に覚えると、比較的簡単に理解することができる。各群(点群も群の一種である)において、全ての対称要素の数を足し合わせたものを、その群の位数(order)とよぶ。
(1) 単純対称群
単純対称の分子は、唯一の対称操作 σ、i 、または C2 のいずれかと恒等操作 E を加えた位数 2 の対称群である。
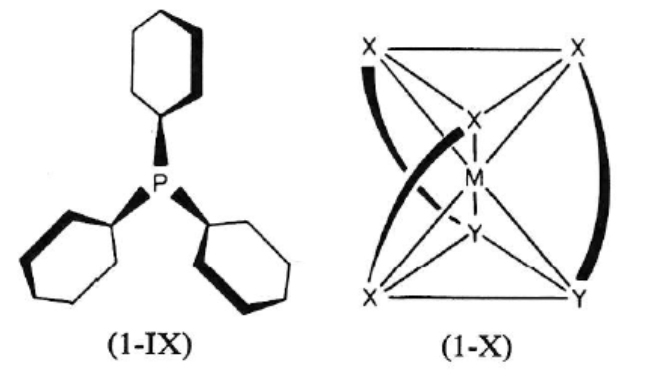
Cs 対称(s: simple)の分子はかなり希な分子で、thionyl halides と sulfoxide(1-Ⅲ)、第二級アミン類(1-Ⅳ)などがある。対称心 i のみを有する分子は極めて希で、(1-Ⅴ)(1-Ⅵ)で示す 2 つの分子群がある。C2 対称の分子はかなり一般的に見られ、(1-Ⅶ)や(1-Ⅷ)などが挙げられる。
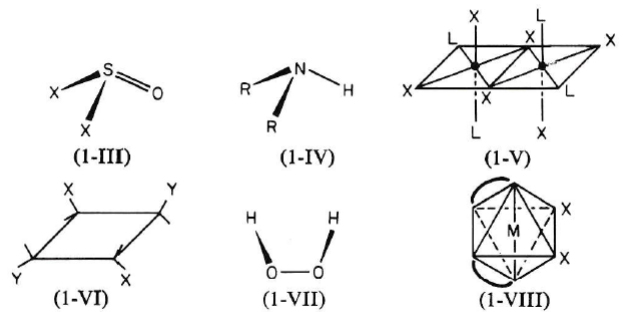
単純対称の分子例
Cs 対称(s: simple)の分子はかなり希な分子で、thionyl halides と sulfoxide(1-Ⅲ)、第二級アミン類(1-Ⅳ)などがある。対称心 i のみを有する分子は極めて希で、(1-Ⅴ)(1-Ⅵ)で示す 2 つの分子群がある。C2 対称の分子はかなり一般的に見られ、(1-Ⅶ)や(1-Ⅷ)などが挙げられる。

単純対称の分子例
(2) Cn 群
(3) Cnv 群
Cn 軸を主軸とし、主軸を含む n 個の対称面 σv だけを有する対称群を記号 Cnv で示す。群の位数は 2n である(Cnn = E であり、E を含むので)。
水分子は C2v 群に属するが、2 回転軸が 1 本で、主軸 C2 を含み、相互に直交する対称面 σv が 2 つあり、恒等操作 E の要素を加えて、位数は 4 である。
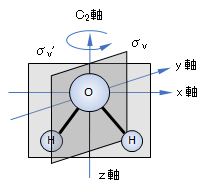
図1 H2O 分子の C2v 対称要素
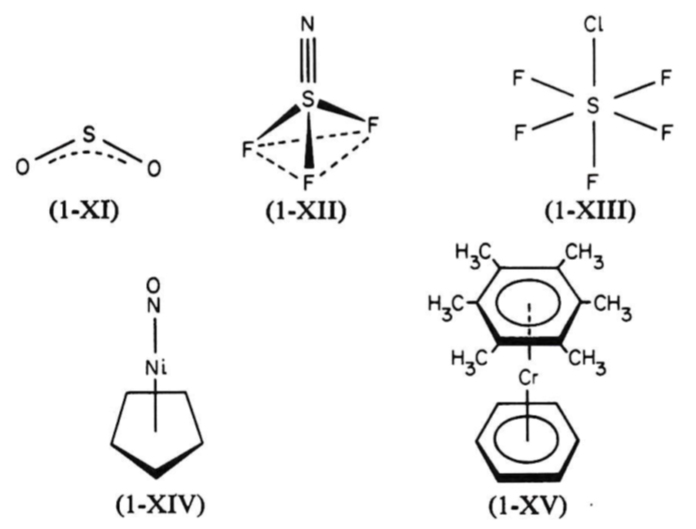
Cnv 対称の分子例
水分子は C2v 群に属するが、2 回転軸が 1 本で、主軸 C2 を含み、相互に直交する対称面 σv が 2 つあり、恒等操作 E の要素を加えて、位数は 4 である。

図1 H2O 分子の C2v 対称要素

Cnv 対称の分子例
(4) Cnh 群
Cn 軸を主軸とし、この主軸に垂直な1つの対称面 σh だけを有する。Cnh 群の位数は 2n である(Cnn = E であり、E を含むので)。この対称群に属する分子は、かなり希である。
事例として、(1-ⅩⅥ)・(1-ⅩⅦ)を示す。
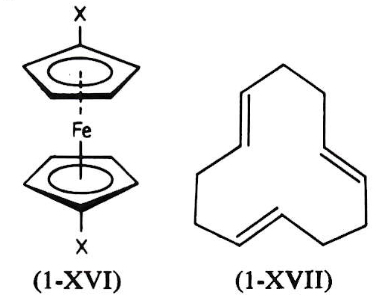
Cnh 対称の分子例
事例として、(1-ⅩⅥ)・(1-ⅩⅦ)を示す。

Cnh 対称の分子例
(5) Dn 群
主軸として Cn 軸を持ち、それに垂直な n 本の C2 軸がある。この点群に属する分子を具体的に考える前に、次の Dnh と Dnd 群の分子を理解し、それらの中間的な構造を有する主軸に対して少しねじれた構造を持つ分子として理解するとわかりやすい。
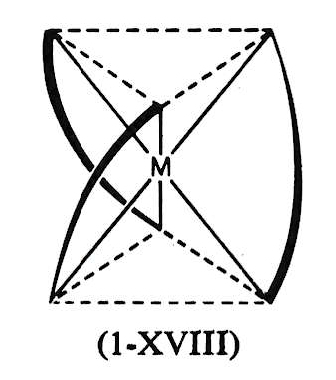
Dn対称の分子例

Dn対称の分子例
(6) Dnh 群
主軸 Cn に垂直な 2 本の 2 回転軸 C2 を持つとともに、主軸に垂直な対称面 σh を有する。
ベンゼン C6H6(D6h)、[PtCl4]2-(D4h)などの平面正 n 角形構造の化合物のほか、次図のような正 n 角柱構造の化合物、上下の環が主軸 Cn に垂直な平面 σh に対して対称的に配置した構造のフェロセゾン(eclipsed configeration)などがある。
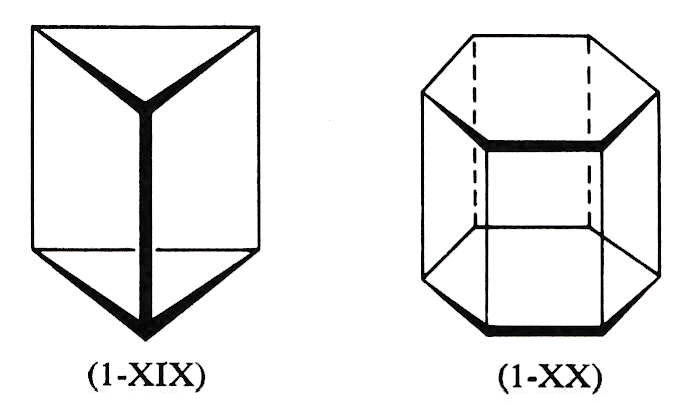
Dnh対称の分子例
ベンゼン C6H6(D6h)、[PtCl4]2-(D4h)などの平面正 n 角形構造の化合物のほか、次図のような正 n 角柱構造の化合物、上下の環が主軸 Cn に垂直な平面 σh に対して対称的に配置した構造のフェロセゾン(eclipsed configeration)などがある。

Dnh対称の分子例
(7) Dnd 群
主軸 Cn に垂直な n 本の C2 回転軸を有し、さらに 2 本の C2 回転軸の間の角を 2 等分する対称面 σ(σd 面と記す)を持つ。
この点群に属する化合物はアンチプリズム型である。すなわち、正 n 角柱の上下の平面がねじれた構造 (stagged configeration) を持つ。
例としては、三角ねじれプリズム (trigonal anti-prism) 構造の エタン(1-ⅩⅪ)、ねじれ型のフェロセン(1-ⅩⅫ)などがある。
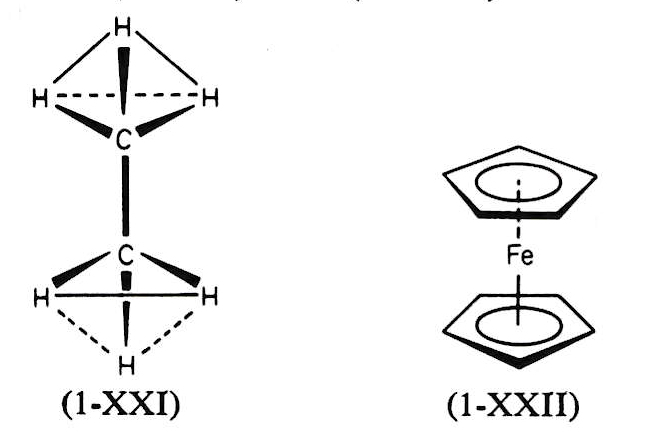
Dnd 対称の分子例
この点群に属する化合物はアンチプリズム型である。すなわち、正 n 角柱の上下の平面がねじれた構造 (stagged configeration) を持つ。
例としては、三角ねじれプリズム (trigonal anti-prism) 構造の エタン(1-ⅩⅪ)、ねじれ型のフェロセン(1-ⅩⅫ)などがある。

Dnd 対称の分子例
(8) Td 群
高い対称性を有する正四面体 Td 群および正八面体 Oh 群は極めて重要なものである。
Td は 24 の対称操作を有する。3 つの S4 軸は、S44(= E) を除いて 3 ✕ 3 = 9 操作、4 つの C3 軸は、C33(= E) を除いて、 4 ✕ 2 = 8 操作を有する。さらに、6 つの σd と E を加えて、合計 9 + 8 + 6 + 1 = 24 の対称操作がある。
完全な Td 対称を有する分子として、CH4、 ClO4–、 Ni(CO)4、Ir4(CO)12 などがあり、少し歪んだ Td 対称分子は多数見られる。
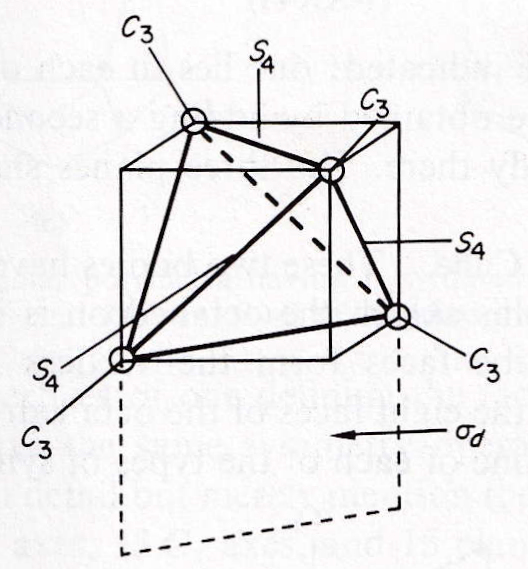
図2 正四面体 Td の対称操作
Td は 24 の対称操作を有する。3 つの S4 軸は、S44(= E) を除いて 3 ✕ 3 = 9 操作、4 つの C3 軸は、C33(= E) を除いて、 4 ✕ 2 = 8 操作を有する。さらに、6 つの σd と E を加えて、合計 9 + 8 + 6 + 1 = 24 の対称操作がある。
完全な Td 対称を有する分子として、CH4、 ClO4–、 Ni(CO)4、Ir4(CO)12 などがあり、少し歪んだ Td 対称分子は多数見られる。

図2 正四面体 Td の対称操作
(9) Oh 群
正八面体は、立方体の中に描くことができ、各頂点は、立方体の6つの面の中心に位置している。対称記号は Oh で示され、下記で説明する 48 の対称操作を有する。Oh は極めて重要な対称群で、SF6、Co(NH4)63-、IrCl6 3-など、Oh 群に属する分子は多数ある。正八面体の中心に位置する元素と各頂点に位置する元素(又は原子団)の結合性(イオン・共有)の差異や、結晶構造の安定化力などの様々な因子が加わると、図4に示すように、分子構造に歪みが生じ、対称性の低下した分子に変化する。
3 つの C4 回転軸を有し、3 ✕ 3 = 9 の操作がある。C44(= E) とし、C44‘(= E)を除く。
4 つの C3 回転軸は、4 つの C3 操作と 4 つの C3‘ 操作を含む。
6 つの C2‘ は相対する辺の 2 つの中点を通る回転軸である。
3 つの σh 面と 6 つの σd 面を加えた 9 つの反映操作がある。
C4 軸は S4 軸でもあり、それぞれ S4、S43(= C2) と S43 の操作を生じるので、3 ✕ 2 = 6 の操作が加わる。
C3 軸はまた S6軸でもあり、S、S63(= i)、S65 の操作を生じる。 i は 1 つとして加算し、 4 ✕ 2 + 1 = 9 の新たな操作が加わる。
以上の操作の合計は 9 + 8 + 6 + 9 + 6 + 9 = 48 となる。
3 つの C4 回転軸を有し、3 ✕ 3 = 9 の操作がある。C44(= E) とし、C44‘(= E)を除く。
4 つの C3 回転軸は、4 つの C3 操作と 4 つの C3‘ 操作を含む。
6 つの C2‘ は相対する辺の 2 つの中点を通る回転軸である。
3 つの σh 面と 6 つの σd 面を加えた 9 つの反映操作がある。
C4 軸は S4 軸でもあり、それぞれ S4、S43(= C2) と S43 の操作を生じるので、3 ✕ 2 = 6 の操作が加わる。
C3 軸はまた S6軸でもあり、S、S63(= i)、S65 の操作を生じる。 i は 1 つとして加算し、 4 ✕ 2 + 1 = 9 の新たな操作が加わる。
以上の操作の合計は 9 + 8 + 6 + 9 + 6 + 9 = 48 となる。
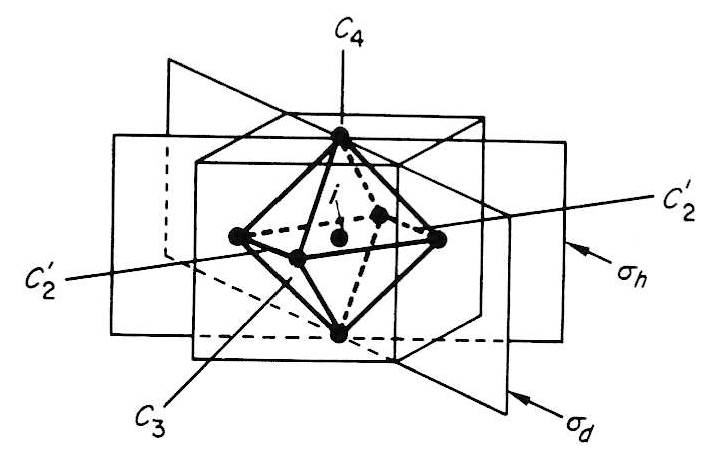
図3 正八面体 Oh の対称操作
(10) Sn 群
他のより高い対称性の帰結としてではなく、純粋に Cn 回転後に、その軸に垂直な面で写映する対称性 σh しか持たない分子群である。この点群に属する分子の例は少ない。
正四面体構造の Td 群の分子群は明らかに S4 軸を持っているが、これは高い対称性の帰結で生じたものであるため、S4 群ではない。
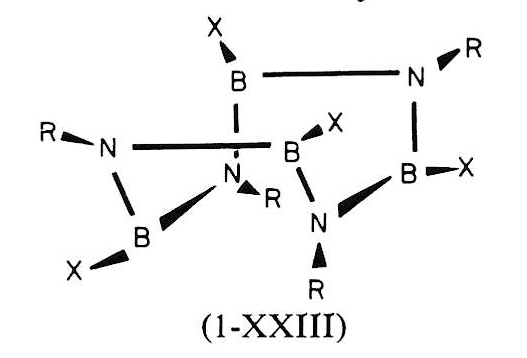
S4 対称の分子例
正四面体構造の Td 群の分子群は明らかに S4 軸を持っているが、これは高い対称性の帰結で生じたものであるため、S4 群ではない。

S4 対称の分子例
(11) 直線状分子の属する点群
(a) 窒素 N≡N やアセチレン CH≡CH のような A-B-B-A 型分子
窒素分子では N-N 結合を左右に貫く主軸があり、それは C∞ 軸である。また、 C∞ 軸に垂直な対称面 σh(窒素分子では、2つの N 原子の真ん中)がある。しかも、主軸に垂直に無限個の C2 回転軸(対称面の中にある)があることがわかる。このような構造は Dnh 群と同じである。ただし、n = ∞ で、このような分子は D∞h 群に属する分子である。
(b) C=O のような A-B-C-D 型分子
C-O 結合は窒素分子と同じように C∞ 軸を有している。しかし、このように左右非対称な分子には C∞ 軸に垂直な対称面 σh はなく、主軸を含む ∞ 個の対称面 σv のみがあるだけである。このような分子は Cnv 型であることがわかる。ただし、n = ∞ になっているので、C∞v 群に属する分子である。
窒素分子では N-N 結合を左右に貫く主軸があり、それは C∞ 軸である。また、 C∞ 軸に垂直な対称面 σh(窒素分子では、2つの N 原子の真ん中)がある。しかも、主軸に垂直に無限個の C2 回転軸(対称面の中にある)があることがわかる。このような構造は Dnh 群と同じである。ただし、n = ∞ で、このような分子は D∞h 群に属する分子である。
(b) C=O のような A-B-C-D 型分子
C-O 結合は窒素分子と同じように C∞ 軸を有している。しかし、このように左右非対称な分子には C∞ 軸に垂直な対称面 σh はなく、主軸を含む ∞ 個の対称面 σv のみがあるだけである。このような分子は Cnv 型であることがわかる。ただし、n = ∞ になっているので、C∞v 群に属する分子である。
これまでに Cn、σ、i、Sn のような対称操作の組み合わせで分子の対称性を見てきた。しかし、Sn という操作は不要ではないかとの疑念が残る。Cn 軸で回してその軸に垂直な面 σ で写映するなら、Cn と σ の操作のみを定義するだけで良いはずである。
Cn、σ、i、Sn の操作は、Cn と σ という 2 種類の回転操作(proper rotation)のみで全て表せるということであり、 なぜ、Sn 操作が必要なのであろうか。
座標(x, y, z)を C2 軸(z 軸とすると)に対して回転すると、 x と y の符号のみが反転するので、この操作後の座標を(-x, – y, z)で表すと、
C2 (x, y, z) = (-x, -y, z)
と書くことができる。同様に、
σh ✕ C2 (x, y, z) = σh (-x, -y, z) = (-x, -y, -z) = S2 (x, y, z)
である。
また、定義から
i (x, y, z) = (-x, -y, -z)
である。
すなわち、S2 は i を表すことに加え、さらに、S1 は σ そのものという重要な結論が得られる。
S2 ≡ i
S1 ≡ σ
この帰結として、Sn を導入することで、上述した proper rotation と improper rotation のいずれであるのか、識別することができる。この識別は、分子の不斉を考える上で、極めて重要な概念である。自分自身の鏡像を重ね合わせることができない分子は不均整(dissymetric)である。無対称 (assymetric) ではないことに気をつけるべきである。
広義 (improper)な回転軸を持つ分子は S1 ≡ σ と S2 ≡ i などの回反軸を持つから不均整ではない。すなわち、不均整とは広義な (improper rotation) 軸を有さない分子に特有の現象であると言える。
これは「対称面あるいは対称心を欠く分子は不均整」とする言い方よりも、ずっと適切であろう。例えば、先に出て来たtetra-methylcyclotetraeneは対称心も対称面も持たないが、S4 軸を持っているので、不均整ではなく、鏡面関係の分子とちゃんと重ね合わせることができる。
Cn、σ、i、Sn の操作は、Cn と σ という 2 種類の回転操作(proper rotation)のみで全て表せるということであり、 なぜ、Sn 操作が必要なのであろうか。
座標(x, y, z)を C2 軸(z 軸とすると)に対して回転すると、 x と y の符号のみが反転するので、この操作後の座標を(-x, – y, z)で表すと、
C2 (x, y, z) = (-x, -y, z)
と書くことができる。同様に、
σh ✕ C2 (x, y, z) = σh (-x, -y, z) = (-x, -y, -z) = S2 (x, y, z)
である。
また、定義から
i (x, y, z) = (-x, -y, -z)
である。
すなわち、S2 は i を表すことに加え、さらに、S1 は σ そのものという重要な結論が得られる。
S2 ≡ i
S1 ≡ σ
この帰結として、Sn を導入することで、上述した proper rotation と improper rotation のいずれであるのか、識別することができる。この識別は、分子の不斉を考える上で、極めて重要な概念である。自分自身の鏡像を重ね合わせることができない分子は不均整(dissymetric)である。無対称 (assymetric) ではないことに気をつけるべきである。
広義 (improper)な回転軸を持つ分子は S1 ≡ σ と S2 ≡ i などの回反軸を持つから不均整ではない。すなわち、不均整とは広義な (improper rotation) 軸を有さない分子に特有の現象であると言える。
これは「対称面あるいは対称心を欠く分子は不均整」とする言い方よりも、ずっと適切であろう。例えば、先に出て来たtetra-methylcyclotetraeneは対称心も対称面も持たないが、S4 軸を持っているので、不均整ではなく、鏡面関係の分子とちゃんと重ね合わせることができる。
3.ショーンフリース記号とインターナショナル記号の対応
これまでに述べた対称操作の表記法は、ショーンフリース記号という。これに対して、結晶学で用いられているインターナショナル記号がある。以下にその対応を説明する。結晶学で使われるインターナショナル記号では 32 個の点群があるが、この表記法は上記で説明したショーンフリース記号と対応している。以下にその対応の様子を示す。
(1) Cn 回転軸について 1, 2, 3, 4, 5, 6 と番号のみで表す。つまり、数字は回転軸(proper rotation)に関する表記である。
(2) 1’, 2’, 3’, 4’, 5’, 6’などの表記はショーンフリース記号における Sn 軸 (improper rotation)に対応している。たとえば、4’ = S4、2’ (= C2 ✕ σh) = i、1’ = σh らである。なお、n’で示した表記法は、本ページの本文のみに使用している記号であって、正記法ではない。正式には、次表に示すように、数字の上部に bar (-) を付記する表記である。HTMLにタグがないので、「’」で示した。
(3) 鏡面 σ を有するときは m で表す。
(a) 鏡面 σv が Cn 回転軸を含む時は nm(例えば 2m など)と書く。
(b) 鏡面 σh が Cn 回転軸と垂直な時は n/m と書く。
n/mmm などと書いてあるときは、m が違う種類の面 σh であることを表す。
ショーンフリース記号の主旨と違って、インターナショナル記号は簡略化が目的であり、必要最小限の情報しか含まれていない。自明の面や軸は書かないルールとなっている。
(2) 1’, 2’, 3’, 4’, 5’, 6’などの表記はショーンフリース記号における Sn 軸 (improper rotation)に対応している。たとえば、4’ = S4、2’ (= C2 ✕ σh) = i、1’ = σh らである。なお、n’で示した表記法は、本ページの本文のみに使用している記号であって、正記法ではない。正式には、次表に示すように、数字の上部に bar (-) を付記する表記である。HTMLにタグがないので、「’」で示した。
(3) 鏡面 σ を有するときは m で表す。
(a) 鏡面 σv が Cn 回転軸を含む時は nm(例えば 2m など)と書く。
(b) 鏡面 σh が Cn 回転軸と垂直な時は n/m と書く。
n/mmm などと書いてあるときは、m が違う種類の面 σh であることを表す。
ショーンフリース記号の主旨と違って、インターナショナル記号は簡略化が目的であり、必要最小限の情報しか含まれていない。自明の面や軸は書かないルールとなっている。
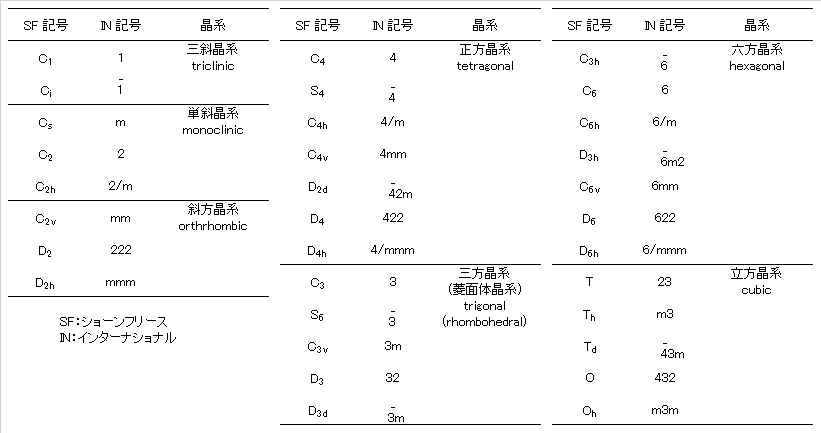
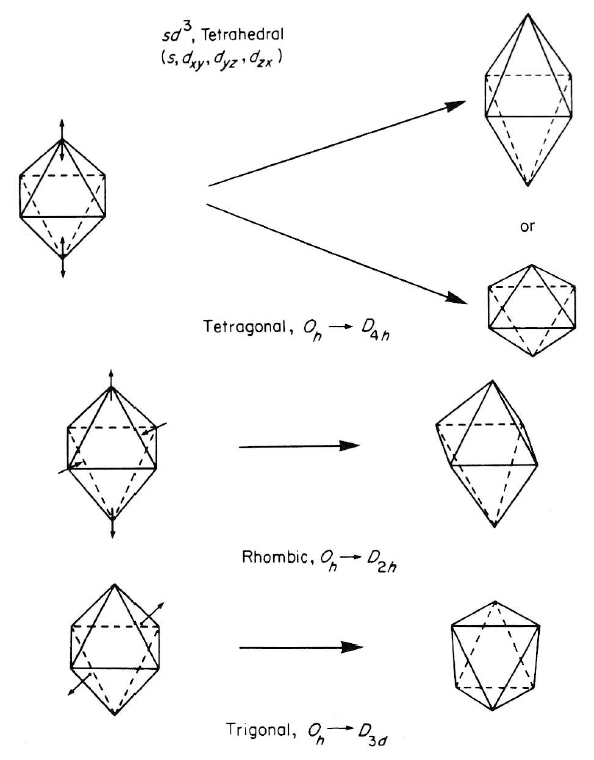
図4 正八面体 Oh の歪み(図中の→方向)と対称性の低下
4.指標表(character table)の構成と読み方
指標表は化学者が群論を用いて議論する上で最も重要なものである。指標表の構成と読み方さえわかれば、群論に関する理解も半ば達成されたと考えられる。
指標表とは「その群に属する分子が持つあらゆる性質(もちろん軌道の対称性も含む)を代表する」表であり、極めて重要なものである。
指標表とは「その群に属する分子が持つあらゆる性質(もちろん軌道の対称性も含む)を代表する」表であり、極めて重要なものである。
水分子は、2.点群表記とその例で説明したように、C2v 群に属する(2 回転軸とその軸を含む 2 つの対称面 σv を持つ)。この群に固有の対称要素は E、C2、σv(H-O-Hを含む面)、σv’(O原子の真ん中を通り、H-O-Hを含む面に垂直な面)である。図1では σv 面は yz 平面であり、σv’ 面は xz 平面としている。
ここで中心となる酸素原子上の 2s、2px、2py、2pz 軌道(表2および図5を参照)を考えると(通常 z 軸を主軸である C2 軸にとる)、例えば 2py 軌道については、各対称操作に対して次のような表ができる。ここでは、各操作によって図5に示しめすように、p 軌道の極性がそのまま保持されれば +1(対称)を、反転すれば -1(反対称)の記号を書くこととする。同様に、各対称操作によって 2px、2pz 軌道と 2s 軌道がどのように変換されるかを調べると次表のようになる。
C2v の対称操作による軌道の変換
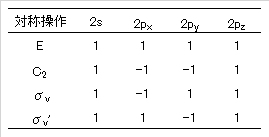
ここで中心となる酸素原子上の 2s、2px、2py、2pz 軌道(表2および図5を参照)を考えると(通常 z 軸を主軸である C2 軸にとる)、例えば 2py 軌道については、各対称操作に対して次のような表ができる。ここでは、各操作によって図5に示しめすように、p 軌道の極性がそのまま保持されれば +1(対称)を、反転すれば -1(反対称)の記号を書くこととする。同様に、各対称操作によって 2px、2pz 軌道と 2s 軌道がどのように変換されるかを調べると次表のようになる。

以上の結果を1つの表にしたものが指標表(character table)とよばれるものである。
一番左上の隅に、点群の記号が、その右にその群における対称要素が書いてある。2 行目以降には、一番左にマリケン記号(Mulliken symbol)とよばれる記号が、その右に各記号に対応する軌道や状態に関する指標(character)が、さらにその右に、対応する軌道を表す表示や、運動状態を表す表示(後述する振動状態の解析に使う)が記述される。
C2v の指標表
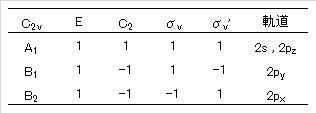
一番左上の隅に、点群の記号が、その右にその群における対称要素が書いてある。2 行目以降には、一番左にマリケン記号(Mulliken symbol)とよばれる記号が、その右に各記号に対応する軌道や状態に関する指標(character)が、さらにその右に、対応する軌道を表す表示や、運動状態を表す表示(後述する振動状態の解析に使う)が記述される。

上記に示した C2v 群の指標表はまだ完全なものではない。それは d 軌道や f 軌道などに関する情報を含んでいないからである。一般的な指標表の例として、C3v 群の指標表を例にとるとわかりやすい。
x, y, z は座標軸であり、Tx,Ty,Tz は各軸方向の並進(transiation)を、Rx,Ry,Rz は、各軸の周りの回転(rotation)を表している。「 z 軸(またはこれと同じ対称性を有する pz 軌道)は A1(全対称)として変換する」という意味である。つまり z 軸ならびに pz 軌道は、C3v群に属する分子では全ての対称操作に対して不変である。また、x と y 軸( px 軌道と py 軌道と言い換えても同じである)は E として帰属され、2 つを分離できない。
量子力学的には、このような 2 つの軌道は同じエネルギーであること(縮重している)を示している。マリケン記号の E に帰属される指標は、2 次元の(数学的には 2 × 2 マトリックスに対応する)表現(representation)であることを示している。さらに z 軸周りの分子の回転 Rz は E と C3 の対称操作ではそれ自身と同じであるが、σv の操作ではその指標が -1 になるという意味も持っているなど、指標表には極めて多くの情報が含まれている。
指標表の最後のカラムは、2 次の座標・軌道の帰属を表している。2 乗あるいは 2 つの 1 次式の積がそれぞれの操作でどのように変換されるかを示している。すなわち、xy, yz, zx などの積や、dxy, dyz, dzx 軌道、3 次元空間内の x2 + y2 という関数の他、dx2-y2 軌道などが、どのようなマリケン記号(軌道や状態を表す記号)に帰属されるかを示している。なお、最後の2つの列をまとめて表記することもある。
x, y, z は座標軸であり、Tx,Ty,Tz は各軸方向の並進(transiation)を、Rx,Ry,Rz は、各軸の周りの回転(rotation)を表している。「 z 軸(またはこれと同じ対称性を有する pz 軌道)は A1(全対称)として変換する」という意味である。つまり z 軸ならびに pz 軌道は、C3v群に属する分子では全ての対称操作に対して不変である。また、x と y 軸( px 軌道と py 軌道と言い換えても同じである)は E として帰属され、2 つを分離できない。
量子力学的には、このような 2 つの軌道は同じエネルギーであること(縮重している)を示している。マリケン記号の E に帰属される指標は、2 次元の(数学的には 2 × 2 マトリックスに対応する)表現(representation)であることを示している。さらに z 軸周りの分子の回転 Rz は E と C3 の対称操作ではそれ自身と同じであるが、σv の操作ではその指標が -1 になるという意味も持っているなど、指標表には極めて多くの情報が含まれている。
指標表の最後のカラムは、2 次の座標・軌道の帰属を表している。2 乗あるいは 2 つの 1 次式の積がそれぞれの操作でどのように変換されるかを示している。すなわち、xy, yz, zx などの積や、dxy, dyz, dzx 軌道、3 次元空間内の x2 + y2 という関数の他、dx2-y2 軌道などが、どのようなマリケン記号(軌道や状態を表す記号)に帰属されるかを示している。なお、最後の2つの列をまとめて表記することもある。

最左列:マリケン記号が入る。 最右列の隣:1次元の座標軸や軌道と座標軸に沿った並進(T)、座標軸周りの回転(R)の帰属が示されている。

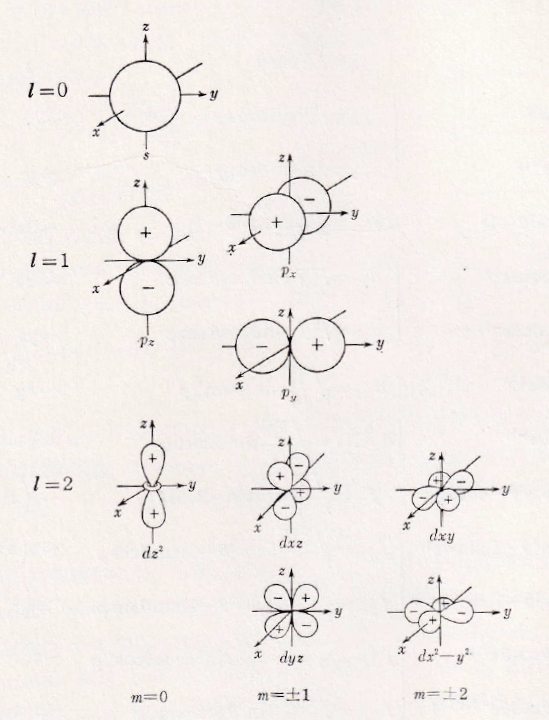
図5 求調和関数で示される電子軌道の形状
マリケン記号の約束
ここでは、マリケン記号の表記に関する約束事を示す。
(1) 1次元の表現(representation)は全て A または B で示す。2 次元の表現は E で、3 次元の表現は T で示す(並進の記号 Tx, y, or ,zと混同しないように、注意する)。数学的には「次元」としてマトリックスの次数を示すが、化学的には軌道や状態の多重度に対応すると考えるとわかりやすい。
(2)主軸である Cn 軸の周りに 2π/n 回転した時に、「もと」と重なるようなときには A(指標が 1 )で示し、同じ操作で「もと」と反対称(指標が -1 )になるものは B で示す。
(3)添字の 1 と 2 は、A や B につけるときは、それぞれ主軸に垂直なC2軸(そのようなC2軸がないときは主軸を含む対称面)に対して対称であれば 1 を、反対称であれば 2 をつける。
(4)A’, B” などの“プライム”記号は σh 面に対して対称的、反対称的であることを示す。
(5) 対称心 i を持てば、反転対称(gerade)なら g を、反転反対称(ungerade)ならば u を付ける。もちろん対称心がなければ何も付けない。
(6) E や T に付ける添字は指標表のコンテンツからは直接決まらないので、一般的には任意の記号と考えておいて差し支えない。
以上、指標表の構成とその読み方について、その要約を説明した。次に、指標表から得られる様々な情報の使い方と、直積という重要な演算法を理解すれば、化学群論の基礎がマスターできたこととなるので、それらの作業手順を解説する。
(1) 1次元の表現(representation)は全て A または B で示す。2 次元の表現は E で、3 次元の表現は T で示す(並進の記号 Tx, y, or ,zと混同しないように、注意する)。数学的には「次元」としてマトリックスの次数を示すが、化学的には軌道や状態の多重度に対応すると考えるとわかりやすい。
(2)主軸である Cn 軸の周りに 2π/n 回転した時に、「もと」と重なるようなときには A(指標が 1 )で示し、同じ操作で「もと」と反対称(指標が -1 )になるものは B で示す。
(3)添字の 1 と 2 は、A や B につけるときは、それぞれ主軸に垂直なC2軸(そのようなC2軸がないときは主軸を含む対称面)に対して対称であれば 1 を、反対称であれば 2 をつける。
(4)A’, B” などの“プライム”記号は σh 面に対して対称的、反対称的であることを示す。
(5) 対称心 i を持てば、反転対称(gerade)なら g を、反転反対称(ungerade)ならば u を付ける。もちろん対称心がなければ何も付けない。
(6) E や T に付ける添字は指標表のコンテンツからは直接決まらないので、一般的には任意の記号と考えておいて差し支えない。
以上、指標表の構成とその読み方について、その要約を説明した。次に、指標表から得られる様々な情報の使い方と、直積という重要な演算法を理解すれば、化学群論の基礎がマスターできたこととなるので、それらの作業手順を解説する。
5.既約表現と直積
C2v の指標表を用いて、指標表の持つ性質を説明する。
上記のマリケン記号の約束から、A1 という表現に帰属される状態や軌道は (1, 1, 1, 1) という指標(ベクトル表現)を有することが分かる。また、B1 表現に対応するものは (1, -1, 1, -1) という指標を持つ。
上記のマリケン記号の約束から、A1 という表現に帰属される状態や軌道は (1, 1, 1, 1) という指標(ベクトル表現)を有することが分かる。また、B1 表現に対応するものは (1, -1, 1, -1) という指標を持つ。

それでは、A1 + B1 という表現に対応する指標というものがあるのだろうか? 全ての対称操作が独立なものであるならば、それぞれの指標を足し合わせることによって A1 + B1 に対応するベクトル表現の指標が表されるはずである。
A1 + B1 = (1, 1, 1, 1) + (1, -1, 1, -1) = (2, 0, 2, 0)
A1 や B1 のような、指標表に現れる表現は既約表現(irreversible representation)とよばれ、それ以上に分割して、他の表現の和や差などに分けることができないものになっている。ここで新しく作った (2, 0, 2, 0) という表現は、可約表現(reversible representation、既約表現の和で表すことのできる表現)となっている。
このことを確かめるために、次のような操作を行う。
まず、(2, 0, 2, 0) に A2 表現が含まれていないことを確かめる。
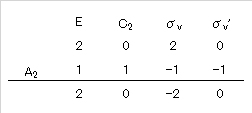
次表に示すように、上下どうしの指標をかけて、横に足すと、2 + 0 – 2 + 0 = 0 となる。
このように、全ての指標を、上下どうしかけ合わせる演算を直積 (direct product) という。ここでは、各群における対称操作が全て独立であるから、各マリケン記号で表される表現間の演算は、それぞれの対称要素に対応する指標どうしの演算になると理解しておけば十分である。
さて、直積をとってできた 4 個の項を全て足し合わせる 2 + 0 – 2 + 0 = 0 となる。このことが、「 (2, 0, 2, 0) (= A1 + B1) 表現は A2 という表現を含んでいないこと」を示していると理解する。ベクトルの内積が 0 になるときには、2 つのベクトルは直交していることと似ている。
指標の直積例-1
A1 + B1 = (1, 1, 1, 1) + (1, -1, 1, -1) = (2, 0, 2, 0)
A1 や B1 のような、指標表に現れる表現は既約表現(irreversible representation)とよばれ、それ以上に分割して、他の表現の和や差などに分けることができないものになっている。ここで新しく作った (2, 0, 2, 0) という表現は、可約表現(reversible representation、既約表現の和で表すことのできる表現)となっている。
このことを確かめるために、次のような操作を行う。
まず、(2, 0, 2, 0) に A2 表現が含まれていないことを確かめる。
次表に示すように、上下どうしの指標をかけて、横に足すと、2 + 0 – 2 + 0 = 0 となる。
このように、全ての指標を、上下どうしかけ合わせる演算を直積 (direct product) という。ここでは、各群における対称操作が全て独立であるから、各マリケン記号で表される表現間の演算は、それぞれの対称要素に対応する指標どうしの演算になると理解しておけば十分である。
さて、直積をとってできた 4 個の項を全て足し合わせる 2 + 0 – 2 + 0 = 0 となる。このことが、「 (2, 0, 2, 0) (= A1 + B1) 表現は A2 という表現を含んでいないこと」を示していると理解する。ベクトルの内積が 0 になるときには、2 つのベクトルは直交していることと似ている。

上記のことを確認するために、(2, 0, 2, 0) には A2 が含まれていることを証明する。先ほどと同様に、(2, 0, 2, 0) と A1 の直積をとってみると次のようになる。
上下をかけて、横に足すと、2 + 0 + 2 + 0 = 4 となる。
直積から得られた結果を横に足すと、今回は 4 である。この値は、C2v 群の位数(全ての対称要素の数)h = 4 に一致している。
群論では、このように直積の結果得られる各項の和が位数の整数 n 倍 [ Σ(直積の各項) = n ✕ h(位数) ] になるとき、「この表現は △△表現を n 回含んでいる」という。この例では、「可約表現である (2, 0, 2, 0) は、A1 表現を 1 回だけ含んでいる」ことがわかる。
指標の直積例-2
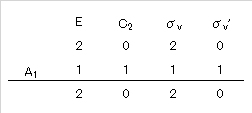
上下をかけて、横に足すと、2 + 0 + 2 + 0 = 4 となる。
直積から得られた結果を横に足すと、今回は 4 である。この値は、C2v 群の位数(全ての対称要素の数)h = 4 に一致している。
群論では、このように直積の結果得られる各項の和が位数の整数 n 倍 [ Σ(直積の各項) = n ✕ h(位数) ] になるとき、「この表現は △△表現を n 回含んでいる」という。この例では、「可約表現である (2, 0, 2, 0) は、A1 表現を 1 回だけ含んでいる」ことがわかる。

参考書
F. A. Cotton, G. Wilkinson: Advanced Chemistry, John Wiley & Sons, pp.3-46, 1972
C. S. Hurlbut, Jr., C. Klein: Manual of Mineralogy, 19th Ed., John Wiley & Sons, pp.12-104, 1977
K. S. Pitzer: Quantum Chemistry, Prentice-Hall, pp.453-456, 1593
大島 勝:群論、共立全書、1954
高木 秀夫:量子論に基づく無機化学、名古屋大学出版会、2010 (本ページの主参考とした)
灰佐 雅夫:構造化学序説(群論化学)、槇書店、1973
吉田 耕作、雨宮 綾夫:応用数学便覧、丸善、pp.59-86, 1967
掲載日:12月03日
更新日: