村上定瞭(水浄化フォーラム)
2.電気泳動法の分類
電気泳動法の略語集
3.代表的な電気泳動法
3.1 アガロースゲル電気泳動法
3.2 アクリロアミドゲル電気泳動法
4.キャピラリー電気泳動法
5.マイクロ・ナノチャンネル電気泳動
キャピラリー電気泳動法-略語集
参考文献
(以下、掲載準備中)
4.キャピラリー電気泳動法
概要
キャピラリー電気泳動(CE)法は、内径 20~100 nmの溶融シリカキャピラリー管内に電解質を含む溶液を充し,電気泳動を行う分離分析技術である。
平板ゲルではなく,極細のシリカ製キャピラリー管を泳動場として用いるこの方法では、最初はキャピラリー中に適当な(ポリマーを含まない)緩衝液を充填したキャピラリーゾーン電気泳動(CZE)法,次いで界面活性剤添加により形成されたミセルへの分配を応用したミセル動電クロマトグラフィー(MEKC)法が普及した。その後にキャピラリー内に分子ふるい篩 効果を持つポリマー溶液を導入する技術が標準化され、高分子試料に特化したサイズセパレーション技術としてキャピラリーゲル電気泳動(CGE)法、さらにタンパク質分析への対応の一環としてキャピラリー等電点電気泳動(cIEF)法が開発され、関連試薬キットも発売されて普及した。
分離後の検出(cIEF法以外は厳密には分離中の検出となる)は、キャピラリー管の中途に設けられた検出窓において紫外/可視吸収の変化、または蛍光強度変化をモニターする方法が採用され、泳動分離後の染色等の作業が不要となった。また泳動前のキャピラリー洗浄・泳動液の導入・試料導入は、複数のバイアルをキャピラリー両端にアクセスできる機構を用いることで自動化された。これらにより電気泳動法を完全自動化・標準化させることが可能となり、様々な検査機器が市販されている。
応用分野
(糖)タンパク質は電気泳動法による分離分析が適した試料であり,CE 法も早い段階から応用された。その成果は現在革新的医薬品として注目されている IgG 抗体医薬品を中心とする生物製剤の開発・試験への応用に結実し,各国の薬局方にも取り入れられた。特に米国薬局方(USP)では,最近,USP 39 Published General Chapter〈129〉Analytical Procedures for Recombinant Therapeutic Monoclonal AntibodiesとしてIgG 抗体医薬品全般を対象とした分析手順が定められ、また、CGE 法による純度試験と糖鎖解析が盛り込まれている。
一方で,CZE/MEKC 法は低分子の無機/有機イオン試料など幅広い分野で応用されている。また分子間インタラクション解析(インタラクションする二つの物質の一方を泳動液に添加し,他方を泳動試料として電気泳動移動度の変化を考察する)などにも応用されている。
解説-電気浸透流
<静圧駆動流>
∇・V = div V = 0 (4-1)
∂V/∂t + (V ・∇)V = -(1/ρ)∇p + ν∇2V + F (4-2)
なお,Vは速度ベクトル、ρは密度(スカラー)、pは圧力(スカラー)、ν(= μ/ρ)は動粘性係数(スカラー)、Fは外場による加速度ベクトルである。左辺について第1項:時間(微分)項、第2項:移流(対流)項、右辺において第1項:圧力項、第2項:粘性(対流項)項、第3:外力項である。
流れ方向への圧力勾配によって駆動される流れを静圧駆動流という。マイクロ流路内では、注入口と出口の水頭差や機械式ポンプによって圧力勾配を発生させることにより流体は駆動される。静圧駆動流はそのメカニズムの簡易さからマイクロ流路内の流体の駆動方法として一般的に用いられている。マイクロ流路内の静圧駆動流のレイノルズ数Reは10-2程度であるため層流となる。
ナビエ・ストークス方程式(4-2)は非線形方程式であるが、定常の静圧駆動流の場合、流路断面形状が単純であれば境界条件から解くことが可能である。内径dの円管内の中心軸に垂直な断面における流体の速度分布Vpr(r)は次式で表される(図4-1)。
Vpr(r) = -(d2/4μ)(dp/dx)(1 – r2/d2) (4-3)
rは中心軸から垂直方向の距離、μは動粘性係数である。
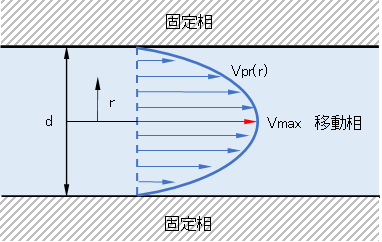
図4-1 静圧駆動よる円筒管内の非圧縮流体断面の速度分布
<電気二重層>
本ページで扱う系は、固体が固定相で、液体(電解質溶液)が移動相である。本節では図4-2に示す電気二重層について説明する。
界面電位Ψoとする平面の法線方向をr軸とし、界面からの距離r[nm]における電位は、次式で近似される。
Ψ(r) = Ψoexp(-κr) (4-4)
この様な電場が溶液相に形成されると、図4-2の左図に示すように、電解質溶液中に分散している荷電粒子の界面近傍の溶液側は拡散電気二重層が形成される。この二重層は、次の相反する2つの作用によって説明される。以下、z-z型対称電解質の溶液とする。
(1) 静電気力によって界面電荷(例えば、負電荷)に対して、正イオンは界面へ近づくように引力が働き、負イオンは遠ざかるように斥力が働くので、図4-2の右図に示すように、界面近傍では正イオン個数(n+、赤線で示す)と負イオン個数(n-、青色で示す)との濃度差Δn(= n+ – n–、緑色の線で示す)が生じる。
(2) 一方で、液中では正負の両イオンは熱運動による拡散力がそれらの濃度差Δnを減少させるように働く。
粒子界面から遠ざかるにつれて静電気力が減衰するのに対し、拡散力は一定であるので、遠く離れたところでは、拡散力が支配的となり正負イオンの個数濃度は等しくなる(n+ → n∞、n– → n∞、Δn → 0; n∞は母液中の正負のイオン数)。
以上述べたように、正負の符号が異なるイオン個数に差が生じると、溶液系のある無限小の体積Δvが電荷を有することになり、その電荷密度ρe[C/m3](= ZeΔn/Δv、eは電子の電荷)と電位Ψの関係は、∇2Ψ = -ρe/ε(ε:溶媒の比誘電率)となる。このような電荷層(液相)に対して外部電場を印加すると、固相が固定されているので、電荷層が電場方向へ移動することとなる。ところが、液体は粘度が高いので、この電荷層に近傍の無電荷層も引っ張れて移動することとなる。これが次節で述べる電気浸透流と言われる現象である。
ところで、電気二重層の厚さはデバイ長λ(= 1/κ)で評価される。固相表面に強く吸着したイオン層は移動できないので、移動する電荷層との境界面が生じる。この境界面をすべり面という。すべりめん面の電位ζをゼータ電位という。固定相表面の電位Ψoは測定できないが、電位ζは測定できる。
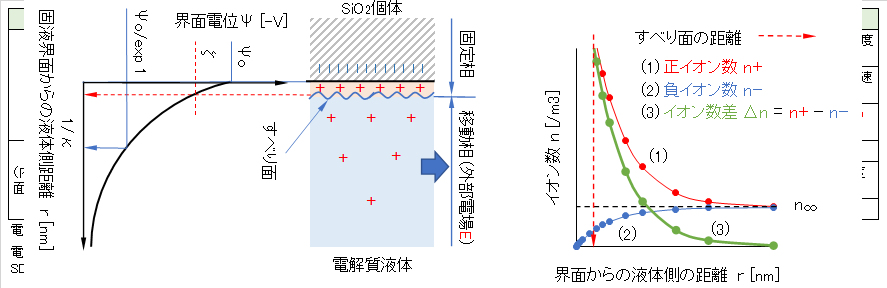
図4-2 表面電荷を有する固液界面の電気二重層構造と外部電場による液相(電解質溶液)のすべり面
<電気浸透流>
① 液相は定常非圧縮性流体とする。
② 圧力項はないものとする(マイクロ流路の注入口と出口の水頭差が等しい)。
③ 慣性項は無視できるものとする(Re数が10-1以下)。
④ 外力項として電気的な力を加える(電気二重層面に対して、平行な直流電場を印加する)。
条件①~④では、式(2.2)に示されるナビエ・ストークス(Navier–Stokes)方程式は,次式のように液相の粘性と電気的な力の釣り合いとして与えられる。
μ∇2V = -ρeE (4-5)
ここで,Vは流れ方向の速度[m/s]、μは粘性係数[-]、ρeは電荷密度[C/m3]、Eは電場強度[V/m]である。
一般的に微小流路で用いられる材質(溶融シリカ、fused silica)の壁面は、中性~アルカリ性では、式(4-6)のように解離して負に帯電するため、ここでは固相壁面が負に帯電している場合を考える。
≡Si-OH ⇄ ≡Si-O– + H+ pKa = 5.3~6.3 (4-6)
x方向を図4-3のように定義すると、流れ方向の速度Vはyのみの関数となる。これより式(4-5)は、式(4-6)に示すポアソン(Poisson)方程式を用いて式(2-7)として展開される。
d2Ψ/dy2 = ρe/ε (4-6)
μ(∂2V/∂y2 )= -ρeE = ε(∂2Ψ/∂y2)E (4-7)
ここで、Ψは固体表面における電位、Eは電界強度、εは流体の誘電率である。y → ∞において∂V/∂y = ∂Ψ/∂y = 0、またV = 0のときのΨ = ζ(固体表面の電位Ψは測定困難であるので、一般的には測定可能なゼータ電位ζで代用する)として式(2-7)を積分すると、次式の電気浸透流速度Veoが得られる。
Veo = -εζE/μ(1 – Ψ(y)/ζ (4-8)
式(2-8)より,電気浸透流速度分布は壁面ではすべりなしの条件から流速が0となり,電気二重層内に非常に急な速度勾配を持つことがわかる。一般の電気泳動用キャピラリーの内径は数十μm程度で、λ/d≒10-4となっている。流路径dとデバイ長λ(= 1/κ、電解質濃度により異なるが数nm程度)の関係から、λ/d<10-4おける壁面近傍の速度勾配は無視できるので,式(2-9)のように一様な速度分布として扱うことができる。この式はHelmholtz-Smoluchowski式とよばれる。
Veo = -εζE/μ (4-9)
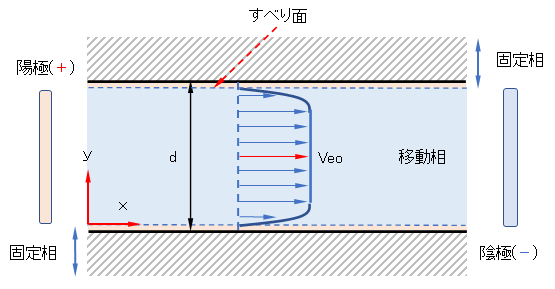
図4-3 表面電荷を有するキャピラりー内の電解質溶液の電気浸透流
(以下、掲載準備中)
公開開始日:2021年12月16日
最終更新日:2021年12月19日
