1.はじめに
電気分解(電解)法を用いた水浄化法の装置の設計・製造・維持管理、電解槽や配管系の材料の選定や上水道/下水道システムにおける設備・送水管・鉄筋コンクリートなどの腐食と防食などにおいて、酸化還元反応における物質間の電子移動に関する速度論的な理解は極めて重要な要素となる。さらに、植物の光合成過程を速度論的に理解する上で[野口 功、2021]、重要な意味があると考えている。
別ページでは酸化還元反応の基礎について説明したが、これは自然界の現象や浄化プロセスを理解する上で重要な知見となるが、実際の浄化プロセス・施設の設計や運転管理を実施するときには、処理装置において単位電極面積・単位時間における水処理量(負荷量)と電力量(電圧×電流×時間)の関係などは、具体的な設計・運転因子となる。ここでは、電気分解モデルを取り上げて、基本的な事項を説明する。
具体的な水浄化における電気化学的プロセスやその計測制御システムについては、別のページで事例を挙げて説明する。
別ページでは酸化還元反応の基礎について説明したが、これは自然界の現象や浄化プロセスを理解する上で重要な知見となるが、実際の浄化プロセス・施設の設計や運転管理を実施するときには、処理装置において単位電極面積・単位時間における水処理量(負荷量)と電力量(電圧×電流×時間)の関係などは、具体的な設計・運転因子となる。ここでは、電気分解モデルを取り上げて、基本的な事項を説明する。
具体的な水浄化における電気化学的プロセスやその計測制御システムについては、別のページで事例を挙げて説明する。
2.電池/電解系のモデル
分かりやすくするため、本ページでは仮想的な電池/電解系を取り上げて、電池/電解系における物質移動(電子を含む)、電気化学的反応の速度について解説する。
(1)電池/電解系の構成
図1に示すように、円筒形の容器(断面積Scm2、長さLcm)の両端に不活性電極としてPt板を装着し、円筒の中央部に隔膜(陰イオンのみ透過する膜)で仕切る。左右の室に活性物質である金属イオンA(A2+ ⇄ A3+)・B(B2+ ⇄ B3+)のそれぞれの錯イオン、AXn(2-n)+ + AXn(3-n)+とBXn(2-n)+ + BXn(3-n)+(A・Bの濃度およびそれぞれの酸化体/還元体の割合は適宜)、および不活性な1-1価の電解質塩YX(Y+ + X–)を共通に含む水溶液を満たす。
左右の電極をリード線で、直流電源、電圧計および電流計に接続する。
左右の電極をリード線で、直流電源、電圧計および電流計に接続する。
(a) 電池/電解系の半反応
活性物質AおよびBの半反応および電位はつぎの通りとし、系内の他の物質との化学反応は起こらず、反応(1)・(2)は可逆的に進行するものとする。
A3+ + e- = A2+ EA = E°A – (RT/F)ln [A2+]/[A3+] (1)
B3+ + e- = B2+ EB = E°B – (RT/F)ln [B2+]/[B3+] (2)
上式において、A・Bについての錯イオンの表記は省略した。以下、特に必要な場合を除いて、同様な表記とする。
B3+ + e- = B2+ EB = E°B – (RT/F)ln [B2+]/[B3+] (2)
上式において、A・Bについての錯イオンの表記は省略した。以下、特に必要な場合を除いて、同様な表記とする。
(b) 電池系と平衡状態
電源回路を切断し、電流計に直列に抵抗を接続すると、電池系が形成される。
今、E°B > E°Aとし、Co = [A2+]o = [A3+]o = [B2+]o =[B3+]oのときには、図1に示すPt(+)からPt(-)に向かって外部回路に電流が流れる。なお、図1および図2は電解系の流れを示しているので、電流i、電子e-の流れ、および各物質の変化を示す各矢印‘→’は、それぞれ、逆方向となる。そして、つぎの式を満たす各物質濃度に達すると、平衡状態(E = 0) となり、電流の流れが止まる。
ln ([B2+]e / [B3+]e) / ([A2+]e / [A3+]e) = (E°B – E°A) F/(RT) (3)
活性物質AおよびBの初期濃度が分かっているので、式(3)より、平衡状態における物質AおよびBの濃度が計算できるが、省略する。
今、E°B > E°Aとし、Co = [A2+]o = [A3+]o = [B2+]o =[B3+]oのときには、図1に示すPt(+)からPt(-)に向かって外部回路に電流が流れる。なお、図1および図2は電解系の流れを示しているので、電流i、電子e-の流れ、および各物質の変化を示す各矢印‘→’は、それぞれ、逆方向となる。そして、つぎの式を満たす各物質濃度に達すると、平衡状態(E = 0) となり、電流の流れが止まる。
活性物質AおよびBの初期濃度が分かっているので、式(3)より、平衡状態における物質AおよびBの濃度が計算できるが、省略する。
(c) 電解系の構成
今、上記(b)の平衡状態から、図1に示すように外部電源に接続し(SWをON)、このときの両電極間の電圧をE[V]としたとき、i[A]の電流が流れることとして、以下の説明を行う。
<本仮想モデルの特徴>
① 多価金属イオンは、弱酸性~アルカリ性領域で水酸化化合物を形成し、沈殿する。そのため、錯イオンを形成させて電解を行う。本モデルでは、上記のようにX-との安定な錯イオン、[AXn](2or3-n)+、[BXn](2or3-n)+を形成し、水酸化物を形成しないものとする。上述したように、これらのA・Bの金属錯イオンを単に、A2+or3+、B2+or3+で表記する。
② 添加する電解質XY(Y++X–)は、酸化還元(電極)反応には、全く関与しないものとする。また、水の電気分解も全く起こらない範囲内の電解系とする。
実際の実験系では、X2ガスあるいは水の電気分解によるH2ガスまたはO2ガスが発生するケースが多いが、本モデルでは、このような反応は生じない範囲内の電池/電解系とする。
③ A2+ + B– = A+ + B2+の反応を防止するために、隔膜は陰イオンX–のみ透過できるイオン交換膜とし、陽イオンの透過は阻止できるものとする。
④ 活性物質AおよびBの各イオンの活量は’1’として扱う。
② 添加する電解質XY(Y++X–)は、酸化還元(電極)反応には、全く関与しないものとする。また、水の電気分解も全く起こらない範囲内の電解系とする。
実際の実験系では、X2ガスあるいは水の電気分解によるH2ガスまたはO2ガスが発生するケースが多いが、本モデルでは、このような反応は生じない範囲内の電池/電解系とする。
③ A2+ + B– = A+ + B2+の反応を防止するために、隔膜は陰イオンX–のみ透過できるイオン交換膜とし、陽イオンの透過は阻止できるものとする。
④ 活性物質AおよびBの各イオンの活量は’1’として扱う。
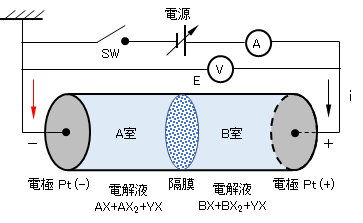
図1 電池/電解系のモデル(各’→’は電解系の流れを示す)
各電極の面積・円筒セルの断面積:S[cm2}、電極間距離:L[cm]、隔膜:イオン交換膜(陰イオンのみ、透過)
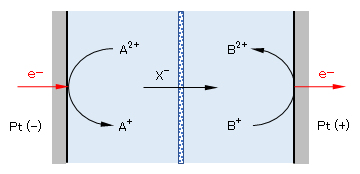
図2 電池/電解の電子移動・物質変化のモデル(各’→’は電解系の流れを示す)
(2)電池/電解系の等価回路
図1に示す電解系のPt(-)面からの距離d[cm](0≦d≦L)の平衡断面における電位φ(d) [V]を示したものが図3である。dAおよびdBは、dSに比べて遙かに小さいものであるが、模式的に示した。3つに区分された部分を以後、di(i=A、S、B)ゾーンとよぶこととする。各ゾーンの具体的な状況(現象または過程)については、下記において詳細に述べる。
今、電極間の電圧E[V]、流れる電流i[V]、各ゾーンにおける抵抗[Ω]をそれぞれRB、RS、RAとし、各ゾーンにおける電圧降下[V]をEA、ES、EBとすると、つぎの関係が成立する。
E = EA + ES + EB = RAi + RSi + RBi
i = E/(RA + RS + RB) (4)
今、電極間の電圧E[V]、流れる電流i[V]、各ゾーンにおける抵抗[Ω]をそれぞれRB、RS、RAとし、各ゾーンにおける電圧降下[V]をEA、ES、EBとすると、つぎの関係が成立する。
i = E/(RA + RS + RB) (4)
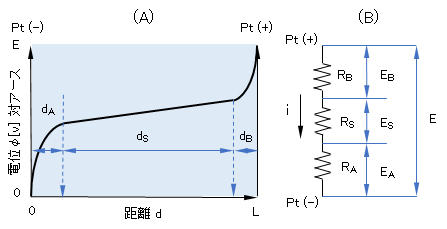
図3 (A) Pt(-)電極からの距離dにおける断面の電位φ(d)、(B)等価電気回路
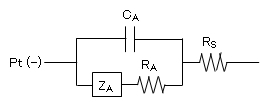
図4 Pt(-)電極近傍における等価電気回路
(3)等価回路から見た律速過程
式(4)において、あるゾーンの抵抗が他のゾーンに比べて極端に大きいときには、つぎの①~③ようになる。式(5)の意味していることは、電解系において、外部から電圧を加えたとき、流れる電流は、抵抗が極端に大きいゾーンによって規制されるということである。このゾーンにおける現象のことを律速過程という。
① RA ≫ RS、RB → i ≒ E/RA
② RS ≫ RA、RB → i ≒ E/RS
③ RB ≫ RA、RS → i ≒ E/RB
(5)
① RA ≫ RS、RB → i ≒ E/RA
② RS ≫ RA、RB → i ≒ E/RS
③ RB ≫ RA、RS → i ≒ E/RB
(5)
3.化学平衡と反応速度
(1)自然電位における平衡状態
ここで、酸化還元反応(1)において、[A2+]i = Cio、[A+]i = Cir、Cio + Cir = 2CT、A2+およびA+の活量係数を’1’とする。
図5(a)において、Cao = Car = CTとすると、
E = E°+ (RT/F)ln (Cao/Car) → E = E° → G = -FE° (5)
A2+ → A+およびA+ → A2+へのそれぞれの反応速度va+およびvb-は、
va+ = ka+Cao exp{-G≠/(RT)}
va- = ka-Car exp{-G≠/(RT)} (6)
平衡状態においては、つぎの関係が成立する。
va+ = va- = va →
ka+Cao = ka-Car = kaCT →
ka+ = ka- = ka (7)
図5(a)において、Cao = Car = CTとすると、
A2+ → A+およびA+ → A2+へのそれぞれの反応速度va+およびvb-は、
va- = ka-Car exp{-G≠/(RT)} (6)
平衡状態においては、つぎの関係が成立する。
ka+Cao = ka-Car = kaCT →
ka+ = ka- = ka (7)
(2)加電圧による平衡状態
自然電位E°に対して、外部からΔEの電圧を加えると、図5(b)のように、A+系のポテンシャルエネルギーはFΔEだけ増加する。この反応系が平衡に達したとき、[A2+]b = Cbo、[A+]b = Cbrすると、式(8)となり、式(9)(10)が得られる。
E°+ ΔE = E°+ (RT/F)ln (Cbo/Cbr) (8)
ΔE = (RT/F)ln (Cbo/Cbr) (9)
Cbo/Cbr = exp{FΔE/(RT)} (10)
A2+ → A+およびA+ → A2+へのそれぞれの反応速度vb+およびvb-は、
vb+ = koCbo exp{(-G≠ – αFΔE)/(RT)}
= koCbo exp{-G≠/(RT)}exp{-αFΔE/(RT)} (11)
vb- = koCbr exp{(-G≠ + βFΔE)/(RT)}
= koCbr exp{-G≠/(RT)}exp{βFΔE/(RT)} (12)
ここで、反応速度の比vb+/vb-は、式(11)/式(12)であるので、これに式(10)とα+β= 1の関係より、式(13)が得られ、さらに式(14)が得られる。
vb+/vb- = (Cbo/Cbr)exp{-(α+β)FΔE/(RT)} = 1 (13)
vb+ = vb- (14)
kb+Cbo = kb-Cbr
kb+ = ko exp{-Gb+≠/(RT)}
kb- = ko exp{-Gb-≠/(RT)}
Gb+≠ = G≠ + αFΔE
Gb-≠ = G≠ – βFΔE
同様に、図5(c)においても、同様に、
vc+ = vc- (15)
kc+Cco = kc-Ccr
kc+Cbo = kb-Cbr
kc+ = ko exp{-Gc+≠/(RT)}
kc- = ko exp{-Gc-≠/(RT)}
Gc+≠ = G≠ – αFΔE
Gc-≠ = G≠ + βFΔE
以上のことから、平衡状態においては見かけ上、反応が進行していないものの、A2+とA+との間で、電子交換反応はある速度vで進行していることとなる。また、ko G≠、αまたはβ、が分かれば、E°(既知)、A2+/A+の濃度およびΔEは実験的に制御できるので、電子交換反応速度vを求めることができる。
<コメント>図2に示すように、電極反応では、A2+が外部からe-を受け取ってA+に変化する、または、その逆の反応が起っている。
しかし、ここで述べている溶液内の平衡状態においては、A2+ + e- ⇆ A+ではA2+がA+へ変化し、A+がA2+へ変化するので、反応の前後において、何も変わっていない。前後の変化のないことに、なぜ、深く立ち入るのかという疑問が残る。この理由は、図5において、(a)→(b)、または、(a)→(c)へ至るまでの途中の過程を理解する上で、平衡状態(a)、(b)、(c)における、それぞれの電子移動反応のメカニズムが重要な知見となるからである。
ΔE = (RT/F)ln (Cbo/Cbr) (9)
Cbo/Cbr = exp{FΔE/(RT)} (10)
A2+ → A+およびA+ → A2+へのそれぞれの反応速度vb+およびvb-は、
= koCbo exp{-G≠/(RT)}exp{-αFΔE/(RT)} (11)
vb- = koCbr exp{(-G≠ + βFΔE)/(RT)}
= koCbr exp{-G≠/(RT)}exp{βFΔE/(RT)} (12)
ここで、反応速度の比vb+/vb-は、式(11)/式(12)であるので、これに式(10)とα+β= 1の関係より、式(13)が得られ、さらに式(14)が得られる。
vb+ = vb- (14)
kb+Cbo = kb-Cbr
kb+ = ko exp{-Gb+≠/(RT)}
kb- = ko exp{-Gb-≠/(RT)}
Gb+≠ = G≠ + αFΔE
Gb-≠ = G≠ – βFΔE
同様に、図5(c)においても、同様に、
kc+Cco = kc-Ccr
kc+Cbo = kb-Cbr
kc+ = ko exp{-Gc+≠/(RT)}
kc- = ko exp{-Gc-≠/(RT)}
Gc+≠ = G≠ – αFΔE
Gc-≠ = G≠ + βFΔE
以上のことから、平衡状態においては見かけ上、反応が進行していないものの、A2+とA+との間で、電子交換反応はある速度vで進行していることとなる。また、ko G≠、αまたはβ、が分かれば、E°(既知)、A2+/A+の濃度およびΔEは実験的に制御できるので、電子交換反応速度vを求めることができる。
<コメント>図2に示すように、電極反応では、A2+が外部からe-を受け取ってA+に変化する、または、その逆の反応が起っている。
しかし、ここで述べている溶液内の平衡状態においては、A2+ + e- ⇆ A+ではA2+がA+へ変化し、A+がA2+へ変化するので、反応の前後において、何も変わっていない。前後の変化のないことに、なぜ、深く立ち入るのかという疑問が残る。この理由は、図5において、(a)→(b)、または、(a)→(c)へ至るまでの途中の過程を理解する上で、平衡状態(a)、(b)、(c)における、それぞれの電子移動反応のメカニズムが重要な知見となるからである。
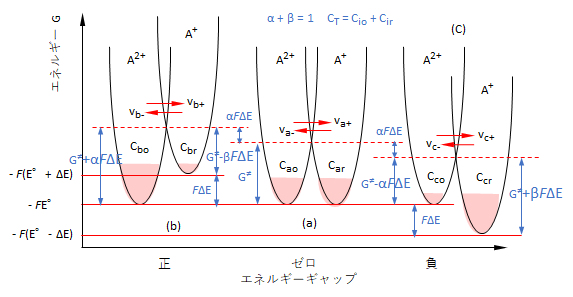
図5 酸化還元系における化学平衡と反応速度
① 放物曲線:中心から力(r:中心からの距離)を受けているA粒子(r,ε)のとεの関係を示す曲線、② ΔG≠: A2+ ⇄ A+系の活性化エネルギー、③ 薄赤:各系(i=a,b,c)にあるA粒子の数Niを視覚的に示している。薄赤で示す領域は、A粒子群(rj,εj)の分布を示していることではない。i系におけるエネルギーεjを持つA粒子数はNj = Ni exp{(-εj/(kT)}で示される*)。④ ①~③で示すεは放物線の底点のエネルギーを基準としたもので、そのエネルギーは図中の縦軸で示してある。⑤ε/(kT) = NAε/(NAkT) = G/(RT)=-nFE/(RT); NA:アボガドロ定数、ε:粒子のエネルギー、G:粒子1モルのエネルギー、E:電位、k:ボルツマン定数、R:ガス定数、F:ファラディー定数、n:粒子の電荷数
*)ここで示す分布関数はボルツマン分布といわれるもので、密度が充分に低く、かつ粒子間の相互作用が無視できような巨視的な物質の挙動についての説明に用いられる。しかし、粒子同士が接近して波動関数が重なって原子や分子間の電子交換が行われるメカニズムなど、ミクロ的な挙動については適用できない。
*)ここで示す分布関数はボルツマン分布といわれるもので、密度が充分に低く、かつ粒子間の相互作用が無視できような巨視的な物質の挙動についての説明に用いられる。しかし、粒子同士が接近して波動関数が重なって原子や分子間の電子交換が行われるメカニズムなど、ミクロ的な挙動については適用できない。
(3)過電圧ΔEと平衡状態の変化
いま、分子系A2+/A+をモデルとして取り上げると、図5(a)の平衡状態では、次式が成立する。
εA2+ + eΔΦ = εA+ (16)
上式において、εjはA2+(aq)およびA+(aq)のエネルギーで、ΔΦは仕事関数はA+とAの仕事関数の差、eは電子の電荷である。上式から理解できるように、εA2+はεA+に比べてeΔΦほどエネルギーが低いことが分かる。陽(金属)イオンが水に溶解した状態では、水分子が配位した錯イオン[A(OH2)m]+/2+を形成し(A2+/A+を分子系とした理由)、さらに分極した水分子層で囲まれている。イオンの電荷数が大きいほど、配位水との結合が強く、さらに分極水層も厚くなって、安定した(エネルギーが低い)状態を保っている。
図5(b)においては、εA+にeΔEのエネルギーを加えているので、εA2+が相対的に低くなり、反応はA2+側に進行することとなる。図5(c)においては、この逆で、A+側に反応が進行することとなる。
上式において、εjはA2+(aq)およびA+(aq)のエネルギーで、ΔΦは仕事関数はA+とAの仕事関数の差、eは電子の電荷である。上式から理解できるように、εA2+はεA+に比べてeΔΦほどエネルギーが低いことが分かる。陽(金属)イオンが水に溶解した状態では、水分子が配位した錯イオン[A(OH2)m]+/2+を形成し(A2+/A+を分子系とした理由)、さらに分極した水分子層で囲まれている。イオンの電荷数が大きいほど、配位水との結合が強く、さらに分極水層も厚くなって、安定した(エネルギーが低い)状態を保っている。
図5(b)においては、εA+にeΔEのエネルギーを加えているので、εA2+が相対的に低くなり、反応はA2+側に進行することとなる。図5(c)においては、この逆で、A+側に反応が進行することとなる。
(4)分子のエネルギー準位εiと活性化エネルギーG≠
前述したように、A2+/A+系において、平衡状態においても、電子交換反応が常に進行していることを示した。
A2+ ⇄ A+、例えば図5(a)ではエネルギー障壁G≠があるが、この障壁をどのようにして乗り越えているのだろうか。
Aイオンには、水分子が配位して錯イオンを形成していることを述べた。錯イオンは回りの水分子に衝突され運動エネルギーを持っている(ブラウン運動のようなもの)。この配位結合(A-OH2)においては、A原子と水分子は振動している。さらに、錯イオン全体の回転、A-OH2の結合軸を中心とする回転がある。また、Aイオンに配位したH2O分子が反転した状態(A-OH2 ⇄ A-H2O)もある。今、m = 6 とすれば、Σ6Ci (i = 1-6) = 64 とおりの配向がある。これはエントロピー(場合の数)と呼ばれる状態エネルギーである。したがって、錯イオン[A(OH2)m]2+/+は様々なエネルギー準位εi (i = 0,1,2,3,・・・) を取ることとなる。
εi = εt + εv + εr + εw + ・・・ (17)
ここで、添え字t、v、r、w、・・・は並進、振動、回転、配向、・・・の各エネルギー準位を示す。さらに各々のεx(x = t,v,w,・・・)、例えば、εvを取り上げると、それはεvj(j = 0,1,2,3,・・・)の準位に分裂している。
1個のAイオンは、離散した様々なエネルギーεiの準位のいずれかを占め、その確率はexp{-εi/(kT)}(k:ボルツマン定数)で示される。εiが大きな値になるほど、指数関数的にその確率は小さくなる。
以上、述べたように、Aイオンは様々なエネルギー準位をとることが可能であり、A2+ ⇄ A+のエネルギー障壁G≠を超えるエネルギー状態があることが理解できる。
A2+ ⇄ A+、例えば図5(a)ではエネルギー障壁G≠があるが、この障壁をどのようにして乗り越えているのだろうか。
Aイオンには、水分子が配位して錯イオンを形成していることを述べた。錯イオンは回りの水分子に衝突され運動エネルギーを持っている(ブラウン運動のようなもの)。この配位結合(A-OH2)においては、A原子と水分子は振動している。さらに、錯イオン全体の回転、A-OH2の結合軸を中心とする回転がある。また、Aイオンに配位したH2O分子が反転した状態(A-OH2 ⇄ A-H2O)もある。今、m = 6 とすれば、Σ6Ci (i = 1-6) = 64 とおりの配向がある。これはエントロピー(場合の数)と呼ばれる状態エネルギーである。したがって、錯イオン[A(OH2)m]2+/+は様々なエネルギー準位εi (i = 0,1,2,3,・・・) を取ることとなる。
ここで、添え字t、v、r、w、・・・は並進、振動、回転、配向、・・・の各エネルギー準位を示す。さらに各々のεx(x = t,v,w,・・・)、例えば、εvを取り上げると、それはεvj(j = 0,1,2,3,・・・)の準位に分裂している。
1個のAイオンは、離散した様々なエネルギーεiの準位のいずれかを占め、その確率はexp{-εi/(kT)}(k:ボルツマン定数)で示される。εiが大きな値になるほど、指数関数的にその確率は小さくなる。
以上、述べたように、Aイオンは様々なエネルギー準位をとることが可能であり、A2+ ⇄ A+のエネルギー障壁G≠を超えるエネルギー状態があることが理解できる。
(5)電子交換速度定数ko
4.分子間での電子移動の条件とその速度
前章3(4)において、Aイオンは様々なエネルギー状態を占めることを示した。それでは、活性化エネルギーG≠を超える状態のAイオンは、どのような条件で、壁を越えてA2+(電子受容体)/A+(電子供与体)の間で、電子の交換(電子の移動)が行われるのであろうか。
異なる原子または分子の間で、電子が移動するには、少なくとも、つぎの3つの条件が同時に満たされなければならない。
① A2+とA+が電子交換できる距離に接近(衝突を含む)すること。
② 供与体A+の電子は、エネルギー障壁G≠を超えるエネルギー状態にあること。
③ 供与体A+の電子軌道と受容体A2+の空軌道のエネルギーレベルが一致すること。
①~③の条件は、それぞれ独立の条件であることから、電子交換速度定数kは、つぎの式で表すことができる。
k = Z・P・exp{-ε≠/(kT)} (18)
ここで、Z はA2+とA+が1秒間の間に電子移動可能な距離に接近(衝突を含む)する確率(頻度)[/s]、P は1秒間にA2+とA+の電子が占めるエネルギー準位が一致する確率[-]、最後の項は移動電子がNAε≠ > G≠(NA:アボガドロ定数)の状態にある確率[-]である。kの単位は[/s]である。
v = kC(C:物質のモル濃度、mol/dm3)の単位は[mol/dm3/s]となり、1L中に含まれるC moleのA2+とC moleのA+が1秒間に v moleの電子交換を行う速度を示している。Z/C の単位は[dm3/mole/s]となり、1L中のそれぞれ1 moleのA2+とA+が1秒間の間に電子交換できる距離(一般的に、10Å以内といわれている)に接近する回数となる。
異なる原子または分子の間で、電子が移動するには、少なくとも、つぎの3つの条件が同時に満たされなければならない。
① A2+とA+が電子交換できる距離に接近(衝突を含む)すること。
② 供与体A+の電子は、エネルギー障壁G≠を超えるエネルギー状態にあること。
③ 供与体A+の電子軌道と受容体A2+の空軌道のエネルギーレベルが一致すること。
①~③の条件は、それぞれ独立の条件であることから、電子交換速度定数kは、つぎの式で表すことができる。
ここで、Z はA2+とA+が1秒間の間に電子移動可能な距離に接近(衝突を含む)する確率(頻度)[/s]、P は1秒間にA2+とA+の電子が占めるエネルギー準位が一致する確率[-]、最後の項は移動電子がNAε≠ > G≠(NA:アボガドロ定数)の状態にある確率[-]である。kの単位は[/s]である。
v = kC(C:物質のモル濃度、mol/dm3)の単位は[mol/dm3/s]となり、1L中に含まれるC moleのA2+とC moleのA+が1秒間に v moleの電子交換を行う速度を示している。Z/C の単位は[dm3/mole/s]となり、1L中のそれぞれ1 moleのA2+とA+が1秒間の間に電子交換できる距離(一般的に、10Å以内といわれている)に接近する回数となる。
(1)頻度因子 Z
気体分子の化学反応では、古くから分子運動と衝突回数の視点多くの理論的・実験的な研究[例えば、Laider, 1963]がある。
一例として、Marcusは電子移動反応速度の理論的研究から、溶液中の中性分離の衝突数として、Z = 1011 dm3/mol/sを提示している(ただし、この値にはPの値も含まれており、電子移動が有効な衝突数である)。
(2)遷移確率 P
ここでは、少し詳しく遷移確率 P の意味について説明する。ここでは、異なる分子の間で電子交換が可能な状態、すなわち、両分子の分子軌道の重なりが生じる距離内に接近しているモデルである。
(a) 分子同士の接近状態
(b) エネルギーの一致
(c)活性状態の形成
5.電解質と溶液抵抗
6.電極表面近傍の電気二重層
7.濃度拡散と物質移動
8.電極-溶液界面での電子移動
9.植物の光合成系での電子移動
10.電解/電池系&光合成系のまとめ
参考文献
一例として、Marcusは電子移動反応速度の理論的研究から、溶液中の中性分離の衝突数として、Z = 1011 dm3/mol/sを提示している(ただし、この値にはPの値も含まれており、電子移動が有効な衝突数である)。
E. Merzbacher, 1970: Quantum Mechanics, John Wiley & Sons.
K.S. Pitzer, 1963: Quantum Chemistry, Prentice-Hall.
C.A. Wert & R.M. Thomson, 1970: Physics of Solids, McGraw-Hill.
市村 浩、1968: 統計力学、裳華房.
井上 鋒朋 訳、1976: 分子衝突と化学反応、学会出版センター.
大堺 利行、他、2013: ベーッシック 電気化学、化学同人.
久保 亮吾、1934: 統計力学、共立全書.
高石 哲男 訳、1966:化学反応速度論 Ⅰ & Ⅱ、産業図書.
電気化学会 編、2002: 電気化学測定マニュアル 基礎編、丸善出版.
広江 克彦、2015: 趣味で量子力学、理工図書.
渡辺 正、他、2008: 電子移動の化学―電気化学入門、朝倉書店.
渡辺 昌、他、1972: 界面電気現象、共立出版.
野口 功 2021: 光の吸収と電子・プロトン移動、光合成(日本子合成学会[編])、pp.29-34、朝倉書店.
掲載日:2018年02月15日(未公開)
更新日:2023年12月09日(公開)
